�@���w�̕����̓ǎ҂̏��w������̖��ł��B
�F����͉����܂����B
��ʌ��̏��w���@�W�F�_ ����̖��ł��B
�y���Q�Q�|�P�z New!!
�`�~�a�|�b���P�U
�b���a�~�`���W
�a�~�b���`���R�Q
�����̎������藧�ł������������`�A�a�A�b�����߂Ă��������B
�y���Q�Q�|�Q�z New!!
���l�ɁA
�`�~�a�~�b���c
�a�~�d���`���e
�c���d�~�`���d
�̏ꍇ�͂ǂ��ł��傤���B
�_�ސ쌧�̏��w���@�Ă�[ ����̖��ł��B
�y���P�z
�S�O�O��������̂т�ɃW���[�X��������ɓ����Ă��܂��B
�`�Ƃa�͂���������݂����̂ł����A
�P�T�O�����ƂQ�T�O�����̃R�b�v��������܂���B
�Q�l�����傤�ǔ��������ނɂ͂ǂ���������ł��傤���H
�y���Q�z
�V���ƂP�P���̍����v���g���ĂP�T�����v�肽���B
���āA�ǂ���������ł��傤�H
�y���R�z�P�@�@�V�@�Q�T�@�@��
�P�@�@�T�@�P�R�@�Q�T
�P�@�@�R�@�@�T�@�@�V
�P�@�@�P�@�@�P�@�@�P
���ɓ��鐔���͂Ȃ�ł��傤�B�i���R���j
�y���S�z
�U�R�~�U�V���S�Q�Q�P
����͂��̂܂ܕM�Z����Γ����o�Ă��܂����A�����ƊȒP�ȕ��@������܂��B
����͏\�̈ʂ��������ŁA��̈ʂ̍��v���P�O�ɂȂ�S�Ă̌v�Z�Ɏg���܂��B
�i�V�Q�~�V�W���T�U�P�U��A�R�U�~�R�S���P�Q�Q�S�ȂǁB�j
���̊ȒP�Ȃ����Ƃ͈�̂Ȃ�ł��傤�B
�y���T�z
���~�X�{���̌v�Z�ɂ��čl���܂��B
�������̂Q�{�̎��͊ȒP�Ȍv�Z���@������܂��B
�i�P�O�O�~�X�{�Q�O�O���P�P�O�O��A�T�Q�R�~�X�{�P�O�S�U���T�V�T�R�Ȃǁj
���̊ȒP�Ȃ����Ƃ͈�̂Ȃ�ł��傤�B
�y���P�Q�z
�y���P�Q�|�P�z
�P�{�P���S
�Q�{�Q���Q
�R�{�R���S
�S�{�S���S
�T�{�T���Q
�U�{�U���S
�V�{�V����
�W�{�W���S
�X�{�X���U
�P�O�{�P�O���U
�i�P�j���ɓ��鐔���͉��ł��傤���H
�i�Q�j����͉��̋K���Ɋ�Â��Ă���ł��傤���B
�y���P�Q�|�Q�z
��{�ꁁ�Q
��{�S
�O�{�O���U
�l�{�l���P�O
�܁{�܁��W
�Z�{�Z���W
���{�����S
���{�����S
��{�ぁ�S
�\�{�\����
�i�P�j���ɓ��鐔���͉��ł��傤���H
�i�Q�j����͉��̋K���Ɋ�Â��Ă���ł��傤���B
�啪���̏��w���@�ׂ��� ����̖��ł��B
�y���U�z
�c���X���A�����P�T���̒����`�̌`�������y�n������܂��B
���̓y�n�ɋ�������܂łR�������ɁA��A���悤�Ǝv���܂��B
�͉��{�K�v�ł��傤���B
�y���V�z
| �P �P�Q |
�C | �P �U |
�C | �P �S |
�C | �P �R |
�C�H�C | �P �Q |
�C�H�C�H�C�H�C�H�C�H�C�P |
���āA�H�ɓ��鐔�͉��ł��傤���B
���ꂼ�ꋁ�߂Ă�������
�É����̏��w���@���Ȃ���� ����̖��ł��B
�y���W�z
���A��A�Z�A��̉Ƒ��S�l�̔N��̍��v�́A���݂X�R�ł��B
���u����Q�ΔN��ł��B�v
��u�P�P�N�O�ɂ́A�Ƒ��݂�ȂłT�P��������˂��B�v
�Z�u�e���Ƃ��������ŁA���̂U�{�����I�v
��u�l���A�Y��Ȃ��łˁI�v
���݂̕��A��A�Z�A��̔N������߂܂��傤�B
���w�Z�S�N���@�������� ����̖��ł��B
�y���X�z
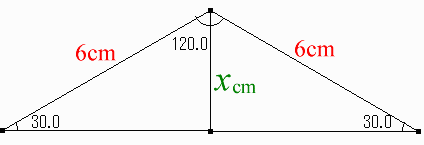
120�x�A30�x�A30�x�̓ӎO�p�`������܂��B
���������̂ق��̕ӂ͂U�Z���`�ł��B
���̎O�p�`�̍����͂Ȃ�ł��傤�B

�啪���̏��w���@�ׂ��� ����̖��ł��B
�y���P�O�z
���̎��͉���\���Ă���ł��傤�B
�y���P�O�|�P�z
�P�{�P���Q
�P�{�P�{�P���R
�P�{�Q�{�R�{�P���Q
�y���P�O�|�Q�z
�S�{�U���P
�U�{�X���Q
�W�{�U�{�X���S
�y���P�P�z
AA*AA=ABBA
���āA����͈ʂ�\���Ă��܂���A��B�͂����炩�ȁH
���A�Ȃ�Ȃ��H
�����ǂ����Ăł��傤�ˁB
�y���P�R�z
����Ƃ���ɂ`�s������܂����B
�ŏ��͐l�����T�O���l�ł�����
�P�N��ɂ͂T��������
�Q�N��ɂ͂P�N�O���T��������
�R�N��ɂ͂P�N�O���T��������
�S�N��ɂ͂P�N�O���T��������
�@�@�@�@�@�@�@�@�@�E
�@�@�@�@�@�@�@�@�@�E
�@�@�@�@�@�@�@�@�@�E
�s���܂����B
���Ă`�s�̐l���͂ǂ��Ȃ�ł��傤��
�_�ސ쌧�̏��w���@�C�k�l�R ����̖��ł��B
�y���P�S�|�P�z
���̂S�̎��͂��錈�܂肪����܂��
7*8=67
5*6=41
13*10=141
12*24=299
�T�C8*12�͂�����ł����
�U�a*5=71�̎��a�̐����͉��ł����
�y���P�S�|�Q�z
���̂S�̎��͂��錈�܂肪����܂��
8#2#12=4
9#6#37=17
12#12#5=139
20#20#20=380
�T�C8#11#9�͂�����ł����
�U�b#9#3=42�̎��b�̐����͉��ł����
�V�c#d#7=56�̎��c��d�͉��ł����
��������Е���9�̔{���łǂ�����P�͓���Ȃ��Ƃ��܂��B
�y���P�T�z
���̐���͂���K��������܂��
3�C1�C2�C8�C3�C1�C3�C0�C3�C1�C3�C0�C3�C1�C3�C1�C3�C0�C3�C1�C3�C0�C3�C1
���̐���͉���\�킵�Ă���ł��傤����������Ă��������
�y���P�U�z
���̎��ɂ͂���K��������܂��
2521*=20�@2742*=112�@7333*=189
(1)4125*�����߂Ă��������
(2)9894*�����߂Ă��������
(3)94255678*�����߂Ă��������
(4)618A*�̓�����96�ɂȂ�܂��
A�ɓ��Ă͂܂鐔�������߂Ă��������
(5)2485B*�̓�����960�ɂȂ�܂��
B�ɓ��Ă͂܂鐔�������߂Ă��������
�y���P�V�z
A�w�ɂ���d�Ԃ��ʂ��Ă��܂��
5�����5�������6������9�����6�������10������16�����10�������17������21�����6�������22���23�����15�������Œʂ��Ă��܂��
(1)���߂��琔����12�Ԗڂ̓d�Ԃ͉��������ł����
(2)���߂��琔����95�Ԗڂ̓d�Ԃ͉��������ł����
(3)14��40�����̓d�Ԃ͏��߂��琔���ĉ��Ԗڂł����
(4)18��24�����̓d�Ԃ͏��߂��琔���ĉ��Ԗڂł����
(5)A�w�ɂ�6������14����܂Ŗ���24���54���A15������21����͖���10���36���ɉ����d�Ԃ��ʂ��Ă��܂��
1���̉�����Ԃ̖{���͉��{�ł�����@
�������A������ԂƏd�Ȃ����d�Ԃ͉^�]���Ȃ��Ƃ��܂��
���w�Z�T�N���@�������� ����̖��ł��B
�y���P�W�z
| �P �� |
+ | �P �� |
�� | �P �Q�S |
��+����98�ł��B
���A���͂��ꂼ�ꂢ���ł��傤�H
�_�ސ쌧�̏��w���@�C�k�l�R ����̖��ł��B
�y���P�X�|�P�z
�1152���10��7488���54��9504���68�ł��
(1)���̂Ƃ���14256��͉��ɂȂ�܂����
(2)�A��̓�����65�ɂȂ�Ƃ��A�͉��ł����
�y���P�X�|�Q�z
�2002��ɂ��Ď��̖�ɓ����Ȃ����
(1)2002��3003�̌��͉�����܂����
(2)2002��3003�̍ŏ����{���͉��ł����
�y���Q�O�|�P�z
1����50�܂ł̐����̒��Ŗ�3���鐮���͉�����܂����
�l�������������������B
�y���Q�O�|�Q�z
1991��A������11�̐����̘a�ŕ\�킹�邱�Ƃ��ؖ����Ă��������
�y���Q�P�|�P�z
�`�~�a���b���U�A
�`�~�a�|�b���P�Q�O�A
�a�{�b���R�Q
�̂Ƃ��R�̐��`��a��b�����ꂼ�ꋁ�߂Ȃ����
�����������������B
�y���Q�P�|�Q�z
�a���b���a�A�`���a���d�A�d�~�d���c�A�`+�d���c
�̂Ƃ���T�̐��`��a��b��c��d�����ꂼ�ꋁ�߂Ȃ����
��������`����E�܂ł̂T�̐��͈قȂ�P���̐����Ƃ��܂��
�����������������B
�@�p���͂�����ł��B
�@�y���̂R�z(NEW!)
�@ ���w�̕����ւ��ǂ�
���w�̕����ւ��ǂ�