���É����@aa ����̉B
�y���P�z
�Z���I�ɂ�(1)�A�ł�(2)�̕����l�Ԗ��������čD���B
(1)
400cc�̂т�250cc�̃R�b�v�ɓ����B
250cc�̃R�b�v����150cc�̃R�b�v�ɓ����B
250cc�̃R�b�v�ɂ́A100cc�c���Ă���̂ŁA�܂�A����������ށB
150cc�̃R�b�v�̒��g���т�ɖ߂��B300cc�ɂȂ�B
�т�250cc�̃R�b�v�ɓ����B
250cc�̃R�b�v����150cc�̃R�b�v�ɓ����ƁA250cc�̃R�b�v�ɂ�100cc�c��̂ŁAA�����ށB
A�́A�s��200cc���̂ŁA�c���B�����ށB
(2)
A�́A400cc�̂т�A200cc�Ǝv����ʂ���250cc�̃R�b�v�ɓ����B
B�́A400cc�̂т�̎c�肩�A250cc�̃R�b�v�̂����ꂩ�����ށB
A�́A�����ɕ���������ɂȂ��Ă���̂ŁAB���ǂ�����Ƃ��Ă��s���͂Ȃ��n�Y�B
B���A�������D���ȕ�������̂ŁA�s���͂Ȃ��B
�y���Q�z
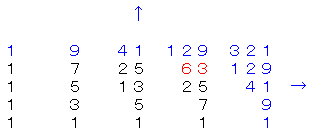
7����11���̍����v���ɂЂ�����Ԃ��B
7���̎��v������������(7���o�ߌ�)����A15�����͂���n�߂�B
4���o�߂���ƁA11���̍����v�̍�����������̂ŁA����Ɠ�����11���̎��v���Ђ�����Ԃ��B
11���̎��v�̍������������_��15�����v���ł���B
�y���R�z
63����?
a b
c d
�̂悤�ɁA������4�̑g�ōl����
b=a+c+d ���K��������?
�y���S�z
(10a+b)�~(10a+c)�̌v�Z�ŁA������b+c=10�B
�ނ���v�Z������ƁA
100aa+10ac+10ab+bc�� 100aa+10a(b+c)+bc������
100aa+100a+bc = 100a(a+1)+bc
����āA�\�̈ʂƏ\�̈ʂ�1�𑫂������̂��|�����킹�����̂ƁA1�̈ʂ��|�����킹�����̂���ׂď����ƁA�|���Z�̌��ʂɂȂ�B
�y���T�z
�u�ȒP�Ȃ����v���Ă̂�key�ł��ˁ`�B
���4�Ɠ����悤�ɂ���ƁA
9a+b = 9a+2a = 11a�Ȃ�ŁAa��10�{�������̂�a�𑫂����Ă����ł��傤��?
�y���U�z
����͖��̈Ӗ����悭�킩��܂���B
�����`�̓y�n�ɁA��A���āA�Ɩ̊Ԃ����Ȃ炸3m�ɂȂ��Ă���悤�ȐA�����Ƃ����Ӗ��ł��傤��?
�y���V�z
����́A12�̐������Ȃ��ł���̂ŁA
| 1 12 |
�C | 2 12 |
�C | 3 12 |
�C...�C | 11 12 |
�C | 12 12 |
����āA?�͍�����A
| 5 12 |
�C | 7 12 |
�C | 2 3 |
�C | 3 4 | �C | 5 6 |
�C | 11 12 |
�y���W�z
���݂̍��v��93�ŁA11�N�O��51�ƌ������́A
���̍���93-51=42�B
4�̔{���ɂȂ��Ă��Ȃ��Ƃ������Ƃ́A11�N�O�ɂ͐��܂�Ă��Ȃ������l������Ƃ������ƁB
�Z�̌��t�������ɁA
| �Z | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| ��+�� | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | 84 | 90 |
�̕\������B
�����_�ł́A��L�̑g�ݍ��킹�̂����ꂩ�̃n�Y�B
���ɁA11�N�O�̏�����B
��L�\�̌Z�����11�������A��+�ꂩ���22�������āA
| �Z | - | - | - | - | - | - | - | - | - | - | - | 1 | 2 | 3 | 4 |
| ��+�� | - | - | - | 2 | 8 | 14 | 20 | 26 | 32 | 38 | 44 | 50 | 56 | 62 | 68 |
��̌��t����A11�N�O��51�ɂȂ�g�ݍ��킹�́A
�Z1�A��+��=50�����Ȃ��B
����āA���݂̌Z�̔N��́A12�B
���݂̕�+���72������A���̌��t���A��37�A��35�B
��́A93-37-35-12�ŁA9�B
���k�C���@�R�W ����̉B
�y���P�z
��l�����傤�ǔ��������ނƂ������Ƃ͂Q�O�Occ����
������̃R�b�v�ŕ�����ɂ́A
�i�菇�P�j
�Q�T�Occ�̃R�b�v�����ς��ɂȂ�܂Œ���
�i�菇�Q�j
�Q�T�Occ�ɂ͂����Ă���W���[�X���P�T�Occ�̃R�b�v�����ς��ɂȂ�܂Œ����B
�i���̎��Q�T�Occ�̃R�b�v�ɂ͂P�O�Occ�̃W���[�X���c���Ă���B�j
�i�菇�R�j
�P�T�Occ�̃R�b�v�ɓ����Ă���W���[�X���r���ɖ߂��A����ɂȂ����P�T�Occ�̃R�b�v�ɂQ�T�Occ�̃R�b�v�ɓ����Ă���P�O�Occ�̃W���[�X������
�i�菇�S�j
�ĂсA�Q�T�Occ�̃R�b�v�ɂ����ς��ɂȂ�܂ŃW���[�X�𒍂��B
�i�菇�T�j
�Q�T�Occ�̃R�b�v�ɓ����Ă���W���[�X���P�O�Occ�̃W���[�X�������Ă���P�T�Occ�̃R�b�v�ɒ����B
��������ƁA�T�O�����̃W���[�X�����P�T�Occ�̃R�b�v�ɂ͒����Ȃ��̂ŁA�P�T�Occ�̃R�b�v�������ς��ɂȂ�܂Œ����ƁA�Q�T�Occ�̃R�b�v�ɂ͂Q�O�Occ�̃W���[�X�������Ă���A���̃W���[�X�Ǝc��̃W���[�X�łQ�O�Occ���̃W���[�X�ɕ�����ꂽ�B
�y���Q�z
�܂��V���̍����v�ƂP�P���̍����v���Ɍv�肾���B
��������Ǝ��R�ɂV���̍����v�̍�����ɗ����Ă��܂��̂ŁA�����ō����v���Ђ�����Ԃ��B
�P�P���̍����v�̍��������I������Ƃ��͂V���̍����v�̍��͂S���Ԃ�̍��������Ă���̂ŁA�����łЂ����肩��������ɂS���v�邱�Ƃ��ł���B
���������
�@�V+�S�i=�P�P�j+�S=�P�T
�ƂȂ�P�T���𑪂邱�Ƃ��ł���
�y���R�z
���̐���ł͎l�p�̐������A�����A���̎O���̘a�ɂȂ��Ă���̂�
���̎l�p�ɂ�
�@�Q�T+�Q�T+�P�R=�U�R�ƂȂ�U�R������B
�y���S�z
�Ⴆ�AAB��AC��������Ƃ���ƁiB+C=�P�O�j
���̉���
�@��̈ʂƕS�̈ʂ̐���A��C�̐��̐ςɂȂ�
�@�\�̈ʂƈ�̈ʂ̐���B��C�̐��̐ςɂȂ�B
���ł����Ȃ邩�͕�����܂���ł����B
�y���T�z
����R���̐����������Ƃ���
�@�������~�X+�Q�~������
���v�Z����ƁA
��̈ʂ͂��A�S�̈ʂ͂�+���A�\�̈ʂ͂�+���A��̈ʂ͂��ƂȂ�܂��B
��+���₂+�����P�O�ȏ�̐��ɂȂ�Ƃ��͂��̂܂܌J��オ���Ď��̈ʂɑ������悤�ł�.
����͂������͂P�O�O��+�P�O��+���Ƃ����A
���̌v�Z��������Ƃ������~�P�P�ƂȂ�A
������₷���悤�Ɍv�Z�����A���A�����ꂼ��ɕ����Ă���
�i�P�O�O��+�P�O��+���j�~�P�P
���P�O�O�O��+�P�O�O��+�P�O�O��+�P�O�� +�P�O��+��
���P�O�O�O��+�P�O�O�i��+���j+�P�O�i��+���j+��
�ƂȂ�A��ŏ��������Ƃ�������܂����B
�y���U�z
�����P�Q�{
�}�������Ă��͂���������܂��B
�y���V�z
���̐���͂`�A�a�A�b�Ƃ�����������ł���Ƃ�
�`+�b=�Q�a�ƂȂ�܂��B
����ɂ��������Čv�Z���Ă����ƁA�����́H���珇��
| 5 12 |
�C | 7 12 |
�C | 2 3 |
�C | 3 4 | �C | 5 6 |
�C | 11 12 |
�ƂȂ�܂��B
�y���W�z
�܂����̌��݂̔N����`
��̌��݂̔N����a
�Z�̌��݂̔N����b
��̌��݂̔N����c�Ƃ����
�`+�a+�b+�c=�X�R�c(1)
�`=�Q+�a�c(2)
�`+�a=�U�b�c(3)
�Ƃ������Ƃ͖�肩�番����܂��B
���ɕ�e�̏،�����P�P�N�O�̔N��̘a���T�P���Ƃ������Ƃ���A
�S���P�P�N�O�ɐ��܂�Ă����Ƃ���ƁA���݂̔N��̑��a����P���ɂS�S���������ɂȂ�͂��������͂Ȃ��Ă��Ȃ��̂ŁA�P�P�N�O�ɂ͒�͐��܂�Ă��Ȃ��ƍl�����܂��B
�Ƃ������ƂłP�P�N�O�̔N��̘a��
�T�P=�`+�a+�b+�c-�R�R-�c�ƂȂ�
��������Ƃ`+�a+�b=�W�S�i(4)�j�ƂȂ�
�c=�X�ƂȂ邱�Ƃ�������
(3)�̎���(4)�̎����
�`+�a+�b=�W�S
�`+�a-�U�b=�O���
�b=�P�Q�ƂȂ�
���Ƃ͎��R�ɂ`=�R�V,�a=�R�T�ƂȂ�
�y���X�z
���̎O�p�`�̏�̒��_���`�A�����̒��_���a�A�E���̒��_���b�A�`������a�b�ɉ��낵�������Ƃ̌�_���f�Ƃ���B
���`�a�����������Ƃa�b�ɐ����Ȑ����b������������Ƃ̌�_���c�Ƃ���ƁA
�p�c�`�b�A�p�`�b�c�̊p�̑傫���͂U�O���ɂȂ�̂ŎO�p�`�`�b�c�͐��O�p�`�ɂȂ�B
�����ł��̎O�p�`�̐��̒����͂`�b=�U�������b�c=�U�����ƂȂ�A
�O�p�`�a�b�c�͎O�p�`�a�f�`�Ƒ����`�ɂȂ�
�O�p�`�a�b�c�͎O�p�`�a�f�`�̂Q�{�̑傫���ɂȂ��Ă��邽��
�`�f�̒����͂b�c�̔����ɂȂ�B
���Ȃ킿�R�p�ɂȂ�B
�i�ʉ��j
�O�p�����g�����������܂�
�`�f=�`�a�~��in�R�O��=�U�~sin�R�O��=�R
�y�R�����g�z
�y���S�z�Ő�̈ʂƕS�̈ʂ̐���A��C�̐��̐ςɂȂ����̂́A���R�ł��ˁB
�Ƃ������A�Ⴊ�U�C�V�ƂV�C�W�ƂR�C�S������ł��ˁB
�y���U�z�͈Ӗ���������ɂ����ł����A����Footmark ����̉��������̂ł͂Ȃ��ł��傤���B
���R�����@Footmark ����̉B
�y���P�z
�W���[�X�̂т�ɂ̓W���[�X�͖߂��Ȃ����̂Ƃ��Ė��������܂��B
(�P)�W���[�X�̂т�P�T�O�t�̃R�b�v�ɖ�����ɓ����B
(�Q)�P�T�O�t�̃R�b�v����Q�T�O�t�̃R�b�v�ɃW���[�X���ڂ��B
(�R)������x�C�W���[�X�̂т�P�T�O�t�̃R�b�v�ɖ�����ɓ����B
(�S)�P�T�O�t�̃R�b�v����Q�T�O�t�̃R�b�v��������ɂȂ�܂�(�P�O�O�t)�W���[�X���ڂ��B
(�T)�P�T�O�t�̃R�b�v�Ɏc����(�T�O�t��)�W���[�X���`�����ށB
(�U)�т�Ɏc���Ă���W���[�X���ׂ�(�P�O�O�t)���P�T�O�t�̃R�b�v�Ɉڂ��B
(�V)�Q�T�O�t�̃R�b�v����P�T�O�t�̃R�b�v��������ɂȂ�܂�(�T�O�t)�W���[�X���ڂ��B
(�W)������ɂȂ����P�T�O�t�̃R�b�v�̃W���[�X���`�����݁A�Q�T�O�t�̃R�b�v�Ɏc����(�Q�O�O�t��)�W���[�X���a�����ށB
�y���Q�z
�V���ƂP�P���̍����v���ɋt���ɂ��܂��B
�V���̍����v���I��������_�łP�P���̍����v�����ɂ��Ď~�߂܂��B
����łP�T�����v�鏀���͂ł��܂����B
�P�P���̍����v�����̂悤�ɗ��ĂďI���܂łS���v��A
�I������炷���t���܂ɂ��ďI���܂łP�P���v��܂��B
���킹�ĂP�T(���S�{�P�P)���ɂȂ�܂��B
�y���R�z
�U�R
�P�ԍ��ƂP�ԉ��͂��ׂĂP�B
����ȊO�́A�������Ƃ��������Ƃ������̐��̍��v�B

�y���S�z
�\�̈ʂ̐��Ƃ��̐��ɂP�����������Ƃ��|���܂��B
��̈ʂ̐����m���|�������̂����̉E�ɕ��ׂ܂��B
�ȉ��͂��̐����ł��B
�Q�̂Q���̐����m�����n�Ɓm�����n�ŕ\���ƁA
�Q�̐��̐�
��{(�����P�O)�{��}��{(�����P�O)�{��}
��{(������)���P�O�O}�{{(�����P�O)��(���{��)}�{(������)
�Ƃ��낪�A(���{��)���P�O �ł�����
�Q�̐��̐�
��{(������)���P�O�O}�{(�����P�O�O)�{(������)
��{����(���{�P)���P�O�O}�{(������)
����́C
�S�̈ʈȏ�̐�������(���{�P)�ŁC
�\�̈ʈȉ��̐��� (������) �ł��B
�y���T�z
�������̂Q�{�Ȃ̂ŁA
���~�X�{�������~�X�{���~�Q�����~�P�O�{��
���Ƃ��̐��������ɂP�����炵�����̂𑫂��ς݂܂��B
�T�Q�R�~�X�{�P�O�S�U �Ȃ�A
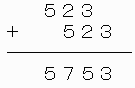
�y���U�z
�c�ɐA���邱�Ƃ��ł���̐�
���X���R�{�P
���S
���ɐA���邱�Ƃ��ł���̐�
���P�T���R�{�P
���U
�A���邱�Ƃ��ł���̍��v�����S���U���Q�S
�y���V�z
| 1 12 |
�C | 1 6 |
�C | 1 4 |
�C | 1 3 |
�C�H�C | 1 2 |
�C�H�C�H�C�H�C�H�C�H�C�P�� |
| 1 12 |
�C | 2 12 |
�C | 3 12 |
�C | 4 12 |
�C | 5 12 |
�C | 6 12 |
�C | 7 12 |
�C | 8 12 |
�C | 9 12 |
�C | 10 12 |
�C | 11 12 |
�C | 12 12 |
| 5 12 |
�C | 7 12 |
�C | 2 3 |
�C | 3 4 | �C | 5 6 |
�C | 11 12 |
�y���W�z
�Z��������݂̕��ƕ�̎��q�Ƃ��Ė��������܂��B
�P�P�N�O�̉Ƒ��S�l�̍��v�N��͌��݂��S�S(���P�P���S)�Ώ��Ȃ����ł��B
�Ƃ��낪�A���ł� �X�R�[�T�P���S�Q�� �� �S�S�ł͂���܂���B
����ƂP�P�N�O�ɂ́A
�u�킾�������܂�ĂȂ������v���A
�u�Z��Q�l�Ƃ����܂�ĂȂ������v�́A�ǂ��炩�ł��B
�u�P�P�N�O�ɂ́A�Ƒ��݂�ȂłT�P��������˂��B�v�ƁA�ꂪ�������Ă���̂ŕ�╃�����܂�ĂȂ����Ƃ͂���܂���B
�P�P�N�O�ɂ́u�Z��Q�l�Ƃ����܂�Ă��Ȃ������v�̂Ȃ�A
�P�P�N�O�ł́A����̍��v�N��͌��݂��Q�Q�Ώ��Ȃ��Ȃ�A
�Z��̍��v�N��͌��݂̂Q�l�̍��v�N������Ȃ��Ȃ锤�ł��B
���ۂɏ��Ȃ������N��͂S�Q�ł�����A
���݂̌Z��̍��v�N��͂Q�O(���S�Q�[�Q�Q)�ł��B
����͂Q�ΈႢ�Ȃ̂ŁA���̍��v�N��͕K�������ŁA����ɌZ��̍��v�N��Q�O(����)�𑫂������ʂ��K�������ł��B
���̂悤�ɁA�X�R(�)�ɂ͂Ȃ蓾�܂���B
�ł�����A�u�Z��Q�l�Ƃ����܂�Ă��Ȃ������v���Ƃ͔ے肳��܂����B
�P�P�N�O�ɂ͒킾�������܂�Ă��Ȃ��������ƂɂȂ�܂��B
�P�P�N�O�ł́A����Z�̍��v�N��͌��݂��R�R�Ώ��Ȃ��Ȃ�A��̔N��͌��݂̔N������Ȃ��Ȃ锤�ł��B
���ۂɏ��Ȃ������N��͂S�Q�ł�����A
���݂̒�̔N��͂X(���S�Q�[�R�R)�ł��B
�ł�����C���݂̕���Z�̍��v�N��͂W�S(���X�R�[�X)�ɂȂ�܂��B
����̍��v�N��͌Z�̔N��̂U�{�ł�����A
�W�S�̂V(���U�{�P)���̂P�̂P�Q���Z�̔N��ɂȂ�܂��B
����ƁA����̍��v�N��͂V�Q(���W�S�|�P�Q)�ł��B
���͕���Q�ΔN��Ȃ̂ŁA
��̔N��͂R�T(��(�V�Q�[�Q)�^�Q)�ŁA
���̔N��͂R�V(���R�T�{�Q)�ł��B
���E��
�ƂĂ��ʔ������ł��ˁB
����Z���l��Ƃ����A
�u�P�P�N�O�̖l�̉Ƒ��̍��v�N��͂T�P�������B�v�Ɩl�ɔ���������ƁA�P�P�N�O�ɖl�����܂�Ă��Ȃ����Ƃ͂Ȃ��̂ŁA�����ƃX�b�L�������̂ł́E�E
�y���X�z
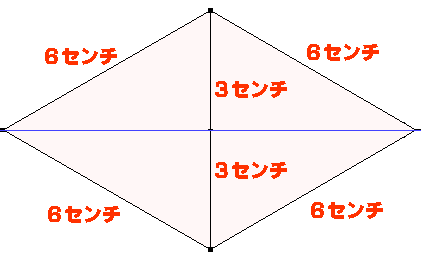
�^����ꂽ�ӎO�p�`�̒�ӂ��牺���ɓ����ӎO�p�`���t���܂ɕt�������܂��B
����ƁA�P�ӂ��U�p�̐��O�p�`���Q�ł��܂��B
���߂鍂���͂��̐��O�p�`�̂P�ӂ̔����Ȃ̂łR�p�ł��B
�y�R�����g�̒lj��z
��l�ڂ̉҂̐É����@aa ����̃R�����g�ł��B
|
�y���U�z�ɂ��� Footmark����̉ł́A �Z �Z �Z �Z �Z �Z�̂悤�Ȑ����`�̌`�Ŗ��Ȃ�Ԃ��ƂɂȂ�܂��B
����ł́A�Ίp����ɂ���̊Ԋu���Rm�ł͂���܂���B |
�ǂȂ����A���̏����ōl���Ă݂܂��B
�������s�̒��w�Z�P�N���@�}�C�N���t�g ����̉B
�y���P�O�|�Q�z
����͐����ɂ���ۂ̐��ł��ˁB
�����ƌ��𑝂₵�Ă݂���H
���R�����@Footmark ����̉B
�y���U�̉��߁z
�u���̓y�n�ɋ�������܂łR�������ɁA��A���悤�Ǝv���܂��B�v
�Ɩ��̒��ŏq�ׂĂ���̂ŁA�S���ɂ͖�A������̂Ɨ�������̂����ʂł͂Ȃ��ł��傤���B
�A����̐��́A�u�ł���������v�Ƃ��u�ł����Ȃ�����v�Ƃ��������Ȃ��̂ŁA�S���ɐA������̂Ɖ��߂��Ȃ���Γ����͍ŏ��{������ő��{���܂ł̕s�����ɂȂ锤�ł��B
�y���U�ŐA�𐳎O�p�`�ɕ��ׂ�ƁH�z
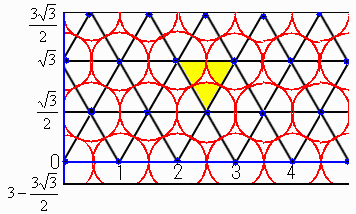
�i�}�ł͂R�����P�Ƃ��Ă��܂��j
�Ɩ̊Ԋu�ɑ��y�n�̏c���������������ꍇ�́A���O�p�`�ɐA����̂��̖{���͍ő��ɂȂ�܂��B
�Ƃ��낪�A���̂悤�ȓy�n�̍L���ł́A���O�p�`�ɐA����Ƃ������Đ����`�ɐA����ꍇ���ő��{���͌������Ă��܂��܂��B
��̐}��������炩�̂悤�ɐ��O�p�`�̏ꍇ�́A
�P�T�{���A������̖{�����Q�Q�{ �ł��B
�������A�ŏ����͐A�̔z�u�ɑ��ēy�n����]�������ꍇ�͊m�F���Ă��܂���B
�y���P�O�|�P�z
�u�P�v�̌����邢�́u�P�ԑ����o�����������v�̌�
�y���P�O�|�Q�z
�u���v�̏o��������
���a�̎R���̒��w�Z�R�N���@�����@��b ����̉B
�y���P�Q�|�Q�z
�����́i�P�j�S�Łi�Q�j�͊������̉搔�𑫂��Ă����Ƃ��̓����ɂȂ�B
���R�����@Footmark ����̉B
�y���P�P�z
�Q�i���ł̕\�L��
�P�P���P�P���P�O�O�P�@�ł�����
�`���P�C�a���O
�y���P�Q�|�P�z
�i�P�j�S
�i�Q�j�����̐����̂��ȕ������̍��v
�@�P�F�����@�i���ȂQ�����j
�@�Q�F�Ɂ@�@�i���ȂP�����j
�@�R�F����@�i���ȂQ�����j
�@�S�F���@�i���ȂQ�����j
�@�T�F���@�@�i���ȂP�����j
�@�U�F�낭�@�i���ȂQ�����j
�@�V�F�����@�i���ȂQ�����j
�@�W�F�͂��@�i���ȂQ�����j
�@�X�F���イ�i���ȂR�����j
�P�O�F���イ�i���ȂR�����j
���R�����@Footmark ����̉B
�y���P�R�z
����C�ӂ̔N�̂Q�N����l���Ă݂��
�@�Q�N��̐l��
��(���݂̐l����1.05)��0.95
��(���݂̐l����0.95)��1.05
�����݂̐l����0.9975
�����݂̐l�� �[ (���݂̐l����0.0025)
�ł�����A�P�N���ɂ͐l���͑������茸�����肵�܂����A
�Q�N���ɂ݂�P�x�������邱�Ƃ͂Ȃ��K���O.�Q�T���������Ă����܂��B
�T�O���l�������`�s�����̓����N�����Ȃ��Ȃ��Ă��܂��܂��l�B
���a�̎R���̒��w�Z�R�N���@coca-cola���݂��[���I ����̉B
�y���P�Q�|�P�z
�y�P�z�����S
�y�Q�z�����̉����̂�������
���a�̎R���̒��w�Z�R�N���@���@�ޓs�� ����̉B
�y���Q�z
�P�T���ɂ���ɂ͂P�P���ƂV���̍����v���ꏏ�Ɏn�߂�B
����ŁA�V���̍����v���I������Ƃ��ɂP�P���̕��́A��S���c���Ă�̂ŁA
�P�P���̍����v�ƁA�c��̂S�������킹�ĂP�T���B
����łł�������B
���a�̎R���̒��w�Z�R�N���@�{�e�@���� ����̉B
�y���P�O�|�P�z
�P�{�P���Q
�P�{�P�{�P���R
�P�{�Q�{�R�{�P���Q
�����P�̐�
���a�̎R���̒��w�Z�R�N���@���@�^�m�q ����̉B
�y���P�Q�|�P�z
�i�P�j�S
�i�Q�j���̐����̓ǂݕ��B
���a�̎R���̒��w�Z�R�N���@�{�e�@���� ����̉B
�y���P�Q�|�P�z
�S������
�y���P�Q�|�Q�z
�搔�Ɋ�Â��ďo���Ă���B
�����Ɍ��̒��w�Z�Q�N���@����� ����̉B
�y���P�O�|�Q�z
���`�Ƃ��肱������
�����̒��ɂ��遛�̐��̍��v���`�`�`�B
���ƁA�v�����Ⴂ�܂����H�H�H
���_�ސ쌧�̒��w�Z�Q�N���@������ ����̉B
�y���P�z
�܂��A250�����̃R�b�v��150�����̃R�b�v��150���������B
�����A250�����̃R�b�v��150�����̃R�b�v��150���������B
��������ƁA250���������t�ɂȂ����Ƃ�150�����̃R�b�v��50�����c��B
�����āA250�����̐����̂ĂĂ����150�����Ɏc���Ă��鐅���ڂ��B
����ŁA250�����̃R�b�v��150�����̃R�b�v��150���������B
�������s�@IKA ����̉B
�y���P�O�|�Q�z
���̐��B�W+�W+�U=�T
����t���̏��w���@������� ����̉B
���͂����āA����ɂP�P�𑫂��B
�y���P�S�|�P�z
�����́A107
���L�����@����@��j ����̉B
���͂����āA����ɂP�P�𑫂��B
�y���P�S�|�P�z
7*8=67
5*6=41
13*10=141
12*24=299
�K�����̐���
�P�j�P�O�i�\�L
�Q�j�u*�v�̉��Z�q�́@���~��+�P�P�Ƃ���ƁA
7*8=67=7�~8+11=56+11=67
5*6=5�~6+11=30+11=41
13*10=13�~10+11=141
12*24=12�~24+11=288+11=299
���̐������������Ƃ���A
�T�C8*12=8�~12+11=107
�U�a*5=71�̎��a�̐����͉��ł����
a*5=a�~5+11=71
a=12
�y���P�S�|�Q�z
8#2#12=4
9#6#37=17
12#12#5=139
20#20#20=380
�K�����̐���
�P�j�P�O�i�\�L
�Q�j��#��#���v�̉��Z�q�́@���~��-���Ƃ���ƁA
8#2#12=8�~2-12=16-12=4
9#6#37=9�~6-37=54-37=17
12#12#5=12�~12-5=144-5=139
20#20#20=20�~20-20=400-20=380
���̐������������Ƃ���A
�T�C8#11#9=8�~11-9=88-9=79
�U�b#9#3=42�̎��b�̐����͉��ł����
b#9#3=b�~9-3=42
b=5
�V�c#d#7=56�̎��c��d�͉��ł����
��������Е���9�̔{���łǂ�����P�͓���Ȃ��Ƃ��܂��B
c#d#7=c�~d-7=56
c�~d=63
(c=9,d=7) ,(c=7,d=9)
����t���̏��w���@������� ����̉B
�y���P�S�|�Q�z
�������́A�u�ŏ��̐��v������u���̐��v�����u�Ō�̐��v�ł��B
�����@�T�D79�C�U�D5�C�V�Dc=9�Cd=7
���_�ސ쌧�̒��w�Z�P�N���@�Ă�[ ����̉B
�y���P�S�|�P�z
���̎��̖@���́A�������̏ꍇ�A�����{�P�P�ł��B
�P�D�W���P�Q�͂�����ł����B
�����@�P�O�V
�W�~�P�Q�{�P�P���P�O�V
�Q�D�����T���V�P�̎�����̐����͉��ł����B
�����@�P�Q
�T���{�P�P���V�P
�T�����V�P�|�P�P
�T�����U�O
�����U�O���T
�����P�Q
�y���P�S�|�Q�z
���̎��̖@���́A�����������̏ꍇ�A�����|���ł��B
�P�D�W���P�P���X�͂�����ł����B
�����@�V�X
�W�~�P�P�|�X���V�X
�Q�D�����X���R���S�Q�̎�����̐����͉��ł����B
�����@�T
�X���|�R���S�Q
�X�����S�Q�{�R
�X�����S�T
�����S�T���X
�����T
�R�D���������V���T�U�̎�����Ƃ��͉��ł����B
��������Е����X�̔{���łǂ�����P�͓���Ȃ��Ƃ��܂��B
�����@�����X�@�����V
�����|�V���T�U
�������T�U�{�V
�������U�R �ƂȂ�B
�U�R�����i�܂��͂��j�������āA���i�܂��͂��j���P�ȊO�̐��ɂȂ�̂́A�����X�̎������B
�U�R���X���V�ŁA�ł��͂V�B
�y���P�T�z
�R�A�P�A�Q�A�W�A�R�A�P�A�R�A�O�A�R�A�P�A�R�A�O�A�R�A�P�A�R�A�P�A�R�A�O�A�R�A�P�A�R�A�O�A�R�A�P
�Ƃ����悤�ɂȂ��Ă���B
���V�����̍��Z���@�ԁi�J�C�j ����̉B
�y���X�z
| sin30���� | �� �U |
| �����U�~sin30�����U�~ | �P �Q |
���R |
�����̏��w���@aaaaa ����̉B
�y���R�z
�����͂U�R�ł��B
���R�́A���̐��i�w�j�́u���̐��A���̐��A�����̐��v�����ׂđ������������̐��i�w�j�ɂȂ��Ă���B
�ڂ��͏��R�ł��B���w���ɂ͏��w���őR�I
�@�y��ꂽ�@���̂Q�z��
�@�w���w������̒����x�ւ��ǂ�