『正三角形の存在』の発展問題です。
【問題】
n次元上、次のようなことを定義します。
【定義1】
点V1(x1,x2,...,xn)と点V2(y1,y2,...,yn)の
距離(D(V1,V2))は
![]()
であることと定義します。
【定義2】
面 P1(a(1,1)*x1+a(1,2)*x2+...+a(1,n)*xn=b1)と
面 P2(a(2,1)*x1+a(2,2)*x2+...+a(2,n)*xn=b2)があります。
a(1,i)=a(2,i) ;i=1,2,...,nであれば
面 P1と面 P2は平行面と定義し、
その時、面 P1と面 P2の距離(D(P1、P2))は
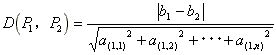
【定義3】
n次元上の(n+1)面体:V0V1...Vnがあります。
すべてのi,j,i≠jに対し、ViVjの距離が等しければ
その(n+1)面体を正(n+1)面体と定義します。
n次元上, n+1平行面があります:
面 P0(a1*x1+a1*x2+...+a1*xn=b0)
面 P1(a1*x1+a2*x2+...+an*xn=b1)
...
面 Pn(a1*x1+a2*x2+...+an*xn=bn)。
このとき各平面上に1点ずつ適当に点を置くことによって,つまり
面 P0上に点V0、面 P1上に点V1、...、面 Pn上に点Vnの条件で
正(n+1)面体V0V1...Vnが存在し、そのViVjの長さ(a)は
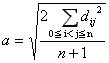
であることを証明してください。
ここで dij=面 Piと面 Pjの距離とします。
【うんちく】
ア)
平行面ではない時は正(n+1)面体V0V1...Vnはいろんな大きさがありますが
(存在しない場合もあります)、
平行面になるとViVjの長さ(a)は一つしかありません。
イ)
面 P1、面 P2、...、面 Pnを同じ面にして(=面 P)、
点V0から面Pまでの距離をbとすると
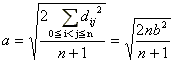
実はbは正(n+1)面体V0V1...Vnの一番短い距離でもあります。
(点V0から面V1...Vnまでの距離です)。
bとaの関係は
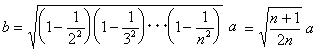
上の式と一致しています。
図の場合、4次元上の正5面体で
![]()
![]()
![]()
| ( | V4X V4V3 | = | 1 ― 2 | , | XY XV2 | = | 1 ― 3 | , | YZ YV1 | = | 1 ― 4 | ) |
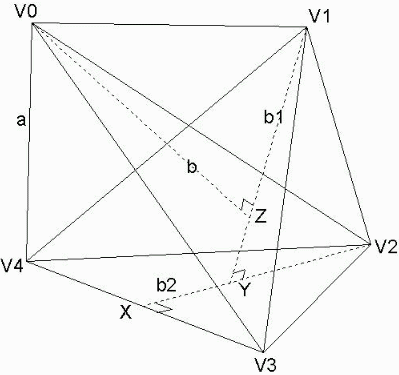
ちなみにV1V2V3V4は3次元上では4面体なのですが、4次元上では平面としか見ら れません。
ウ)
n次元上の多面体の要素を考慮します。
0次元上の平面の数をN0 (=1)
1次元上の平面の数をN1
...
n次元上の平面の数をNn
n+1次元上の平面の数をNn+1 (一つの多面体なので=1)とすると
N0-N1+N2-N3+...+(-1)n+1Nn+1=0という関係(n次元オイラー定理)が得られます。
n次元上のn+1面体の場合はNr=n+1Crから
| n+1 Σ r=0 | (-1)r・ Nr= | n+1 Σ r=0 | (-1)r・ n+1Cr=0。 |
図の場合、
N0-N1+N2-N3+N4-N5 =1-5+10-10+5-1 =0ちなみに3次元の場合は
N1=V,N2=E,N3=F と置き換えると
V-E+F=2
つまり(3次元)オイラー定理が得られます。
すなわち V-E+Fが2であることは偶然ではありません!
◆図形問題へもどる
 数学の部屋へもどる
数学の部屋へもどる