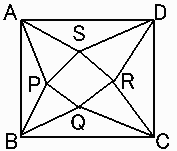
【問題１】
正方形ABCDの各頂角の3等分線を引き、図のようにP,Q,R,Sを定めると、四角形PQRSは正方形であることを示しなさい。
※参考 『正三角形の証明』
【問題２】
四角形ABCDの各頂角の3等分線を引き、図のようにP,Q,R,Sを定める。
四角形PQRSが正方形の場合、四角形ABCDは正方形であると言えるか？
言える場合はその理由を、言えない場合は反例を示しなさい。
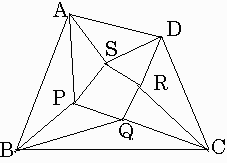
【発展問題１】
上記問題２で四角形PQRSの形状が菱形、長方形の場合、四角形ABCDの形状を答えなさい。
【発展問題２】
一般に、N角形の各頂角の3等分線を引き、隣あう頂角の3等分線の交点のうち、それら頂角をはさむ辺に近い方の交点を順に結んでできるN角形が正N角形の場合、元のN角形は正N角形であると言えるでしょうか？
もちろんご存知なようにN=3の時は成立しません。
◆図形問題へもどる
数学の部屋へもどる