◆愛知県 Y.M.Ojisan さんからの解答
【問題１】
９０度回転に対して対称である。従って、ＰＱＲＳは正方形である。
【問題２】
反例あり：ＡＢＤが直角２等辺三角形でＣがＢＤの中点
なお、自明な正方形とこの反例以外には存在しない。証明は後述する。
（注記） ４角形ではないので反例というべきか若干微妙ですが、正方形でないという方を重視した。
【発展問題１】
少なくとも 自明な形以外のものがある。これで全てかどうかは未確認である。
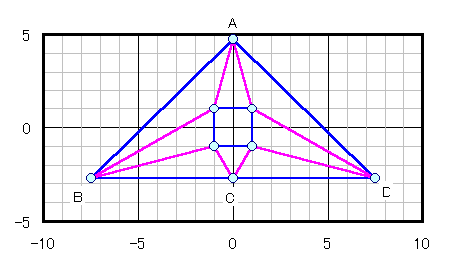
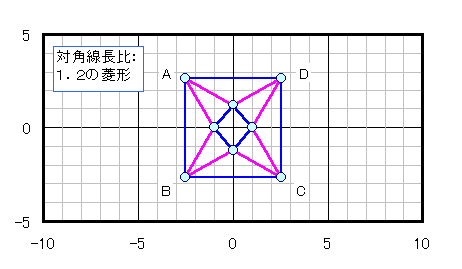
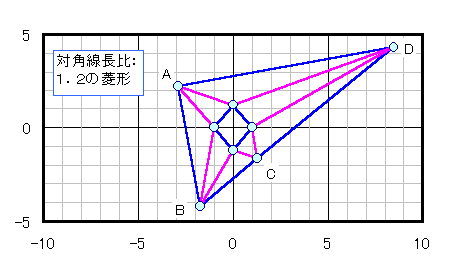
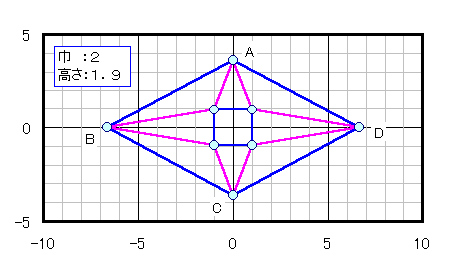
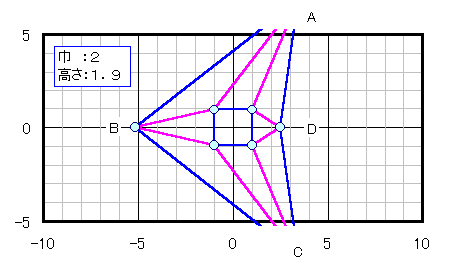
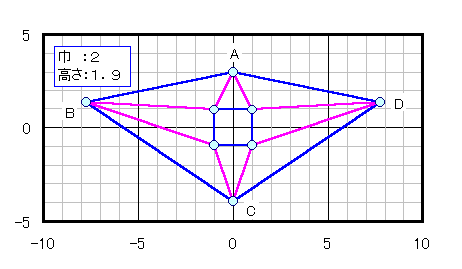
菱形の場合： 自明な長方形（下図参照） ないし 直角３角形（下図参照 ＣはＢＤ上）
 |
 |
 |  |
 |
【発展問題２】
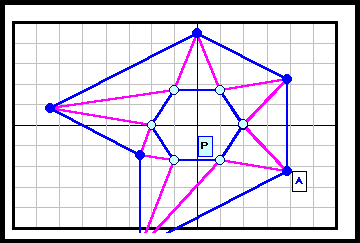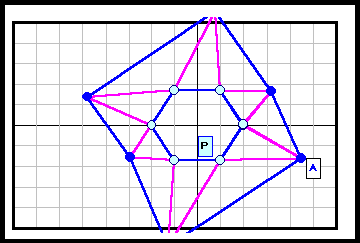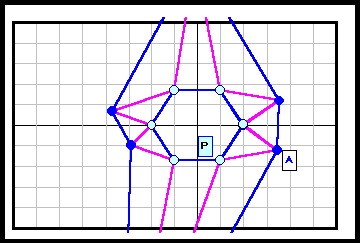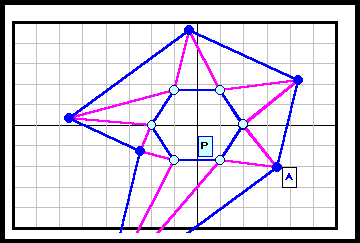
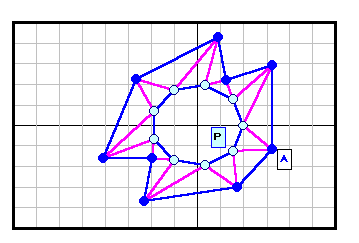
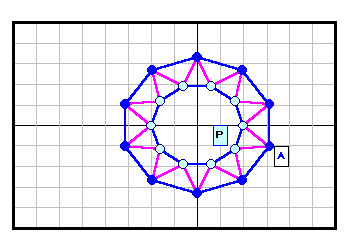
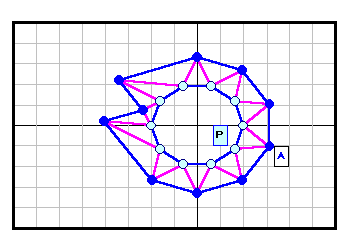
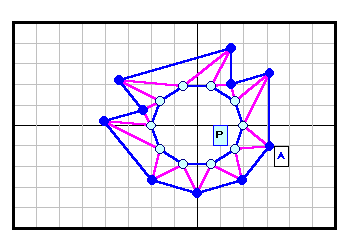
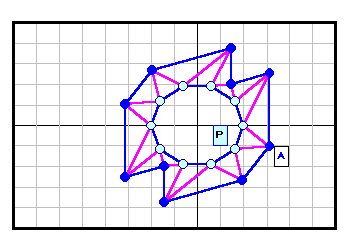
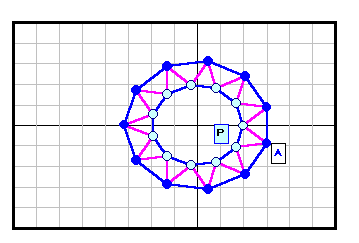
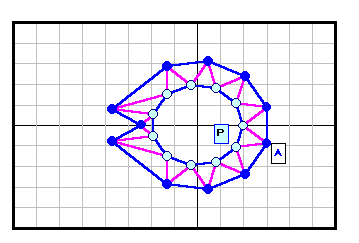
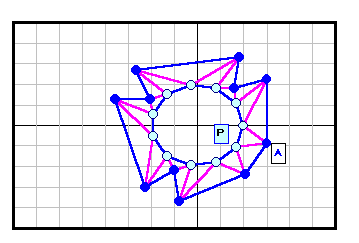
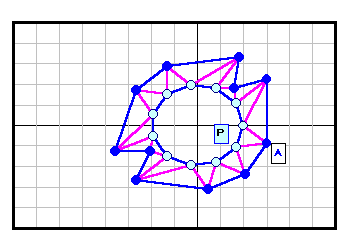
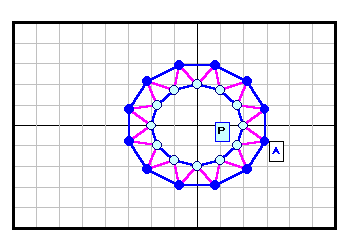
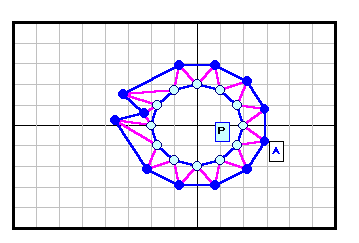
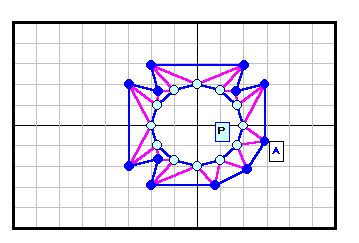
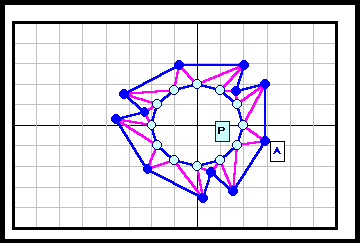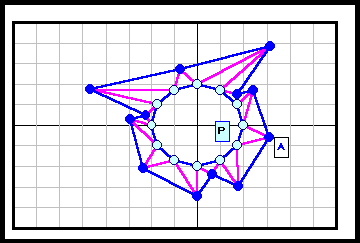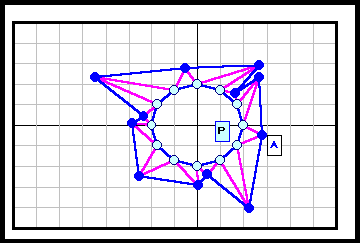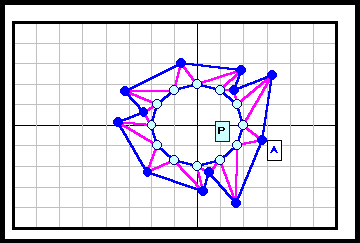
正Ｎ角形以外である反例がある。下図参照 ５角形〜１２角形の場合を示す。
３の倍数角形の場合は自由度が大きく（Ｒ２）、６角形と１２角形の４列目（（順逆逆順）３）の場合についてのみ動画で示す。
なお、証明と「。順逆逆順。」の意味は後段参照。
| N | 逆逆逆逆。。。＝自明解 | 。。。順逆逆順。。。＝反例解 | 。。。順逆逆逆。。。逆逆順。。。 | 。。。順逆逆順順逆逆順。。。 等 |
| 5 |  |
 |
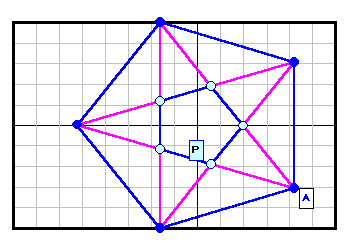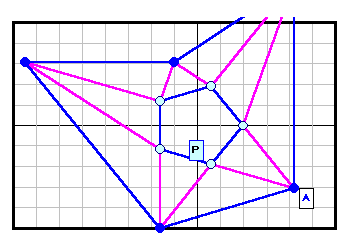なし | なし |
| 6 |  |
 |
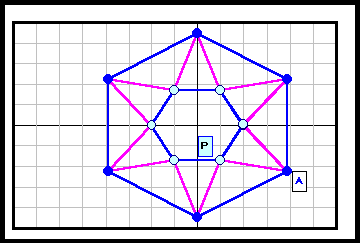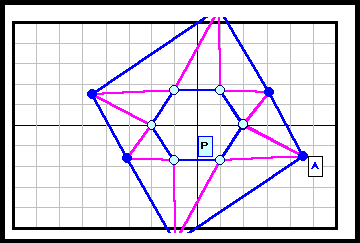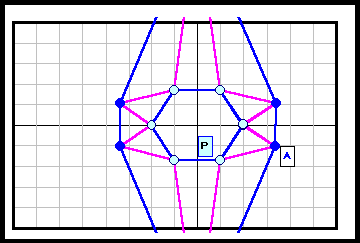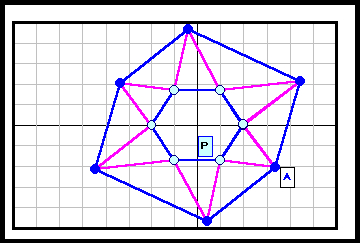なし | なし |
| 7 |  |
 |
 |
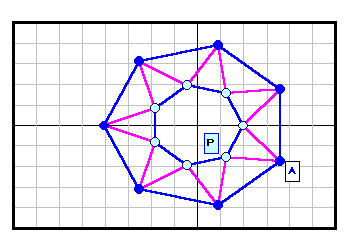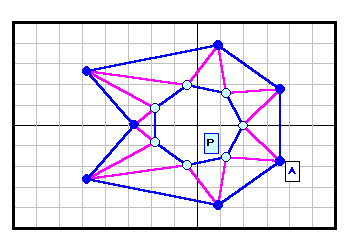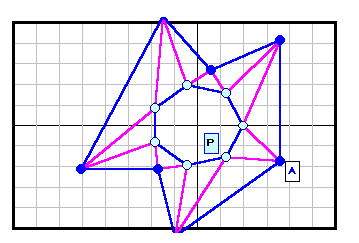なし |
| 8 |  |
 |
 |
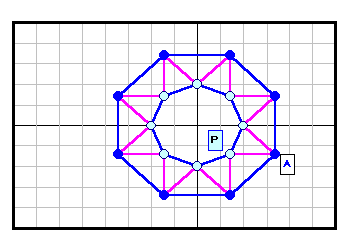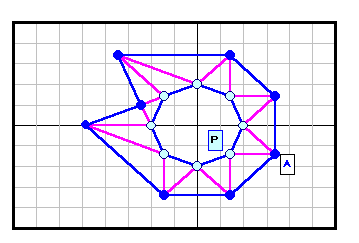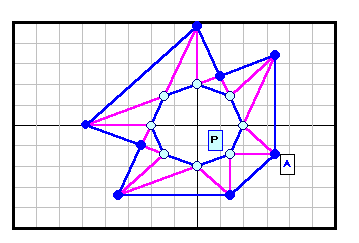なし |
| 9 |  |
 |
 |
 |
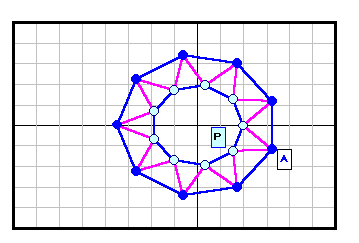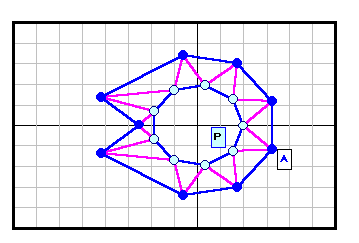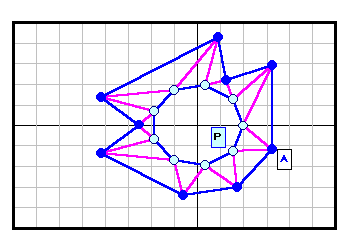| 10 |  |
 |
 |
 |
| 11 |  |
 |
 |
 |
| 12 |  |
 |
 |
 |
∵
【準備：隣接頂点間の関係】（１） 円Ｏを中心とする円周上に等間隔に点ＰＱＲを取ります。また、各辺の中心角をθとする。
（２） 点ＡをＰＱに対してＯの反対側に適当に取ります。
（３） ＰのＱＡに対する対称点をＰ’とします。
（４） ＡＰ’を通る直線とＱを中心とし半径ＱＰの円とのもう一つの交点をＲ’とします。
（５） ＲＰ’の垂直２等分線とＡＰ’を通る直線との交点をＢ+、
（６） ＲＲ’の垂直２等分線とＡＰ’を通る直線との交点をＢ-とする。
この時、∠ＱＡＰ＝∠ＱＡＰ’ ∠ＱＢＲ＝∠ＱＢＲ’ である。ここで Ｂ＝Ｂ+ 又は Ｂ-
であって、Ａ、Ｂは本問題の外側の図形ＡＢＣＤ．．．の隣接頂点間の持つべき関係にある。
ただし、その関係はＢ+ 又は Ｂ-の２通りあり、以後 ＋：順接、−：逆接 とぶ。
また Ｂ+＝順接（Ａ，θ） Ｂ-＝逆接（Ａ，θ） と表すこととする。
（注記） ＡＢＣＤ．．が自明な正Ｎ角形の場合、全て逆接である。
図１ 隣接頂点間の関係
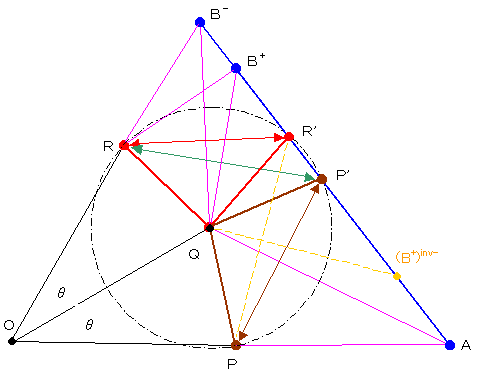
また、点Pを Oを中心に角度α回転させる操作を 回転（P、α）で表すとする。
【補題１：３回隣接頂点間の関係】逆接（逆接（逆接（Ａ，θ),θ),θ)＝回転（Ａ、-３θ） −−−（a）
（１）一般性を失わず 点P、Q、Rの座標を (u,-v) (1.0) (u, v) ここで u=(1-D2)/(1+D2) v=2D/(1+D2) とする。
（２）Aの座標を(x,y)とする。
（３）Ｔ(A)=回転（逆接(A,θ）,−θ）とすれば （a)式は T(T(A))=(T(A*))* −−−(b) と等価である。
ここで*はＱＯＰの２等分線対称な点を表す。
Ｔ(A)を フリーの数式処理ソフトMaxima-Primerにより計算すると ｘ、ｙ、Dの整数係数有理多項式が得られる。即ち、Dの４次、x,yの同次３次以下の有理多項式で下記である。
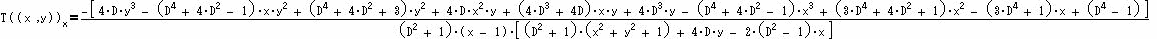
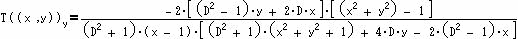
さらに、これを用いてＣ’＝（Ｃｘ，Ｃｙ）＝T((T(A)) を計算すると、
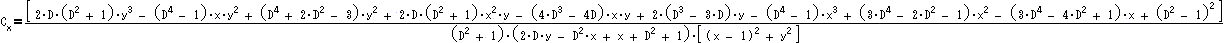
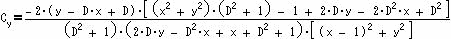
一方、Ｃ’’＝(T(A*))*を計算すると同じ値が得られる。即ち、（ｂ）が成立している。
なお、試しにT(C)も計算させたら、意外に早く計算できて、＝（ｘ、ｙ）＝Ａとなり、(a)でも証明できた。
Maximaへのコマンド（バッチファイル）下表に示す。
また、計算結果を下表に示す。
【補題２：変形法】逆接→逆接→逆接→逆接 ＝ 順接→逆接→逆接→順接 ＝逆接 である。
∵
（１）補題１より 逆接→逆接→逆接＝恒等である。よって、逆接→逆接→逆接→逆接＝逆接である。
（２）補題１より 逆接→逆接＝逆接ー１である。よって、順接→逆接→逆接→順接＝順接→逆接ー１→順接である。これを図１でみると、Ａ→Ｂ＋→(Ｂ＋)inv-→Ｂ- である。従って、順接→逆接→逆接→順接＝逆接である。
【補題３：唯一性】逆接＝恒等 となるＡは一点のみ。
∵ ここでは Ｂ＝Ｂ−とする。
図１において ＡとＢがそれぞれＰＱ，ＱＲに対して相対的に同じ位置にあると言う主張である。
従って、凾`ＱＰ≡凾aＲである。これより∠ＱＡＢ＝∠ＱＢＡであって、ＱＢ＝ＱＡ＝ＰＡである。
すなわち、Ａは∠ＱＯＰの２等分線上である。
Ａが２等分線上をＰＱ上から外に移動してゆく時、∠ＰＡＱは １８０度→０に単調に減少する。一方∠ＱＡＢは負の値→９０度−θ/2に単調に増加する。したがって解は高々１個であって、それは自明な正多角形の場合である。
因みにこれを計算すると、ＰＱＲ．．の外接円の半径を１とするとき、点ABC..は中心Oから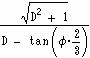の位置である。ここで D=tan(ф) ф＝(90-180/N) 度 である。
【まとめ】
（１）補題３より、少なくとも逆接のみで構成された自明な正多角形のABCD。。。が１個存在している。
（２）補題１の性質により、PQR。。。が３の倍数の正多角形の場合、A点をR２のクラスで自由に選べるABCD。。。が存在している。
（３）補題２により （１）ないし（２）で作成されたＡＢＣＤ。。。をベースに、逆接が連続して３ｍ＋１個ある間は、これを順接＋逆接３ｍ−１個＋順接に置き換えてＡＢＣＤ。。。を作ることが可能であり、これは正多角形ではない。ただしｍは自然数である。最小はｍ＝１のときの４であり、４角形以上で正Ｎ角形でないもの作ることが可能である。
（注記） 少なくとも以上の反例があるとと主張しているだけである。その他にあるかも知れない。
【問題２ ４角形の場合の証明】
P：:(-1,1),Q：(1,1),R：(-1,1),S：(-1,-1) とし A：(Ax,Ay) B：（Bx,By) とし R'とP'の中点をM'とする。
図１に従って、θ＝９０度の場合を計算をすると、下記の結果が得られた。実際の計算は次の手順である。
（１）QAを対称線としてP'を求める。
（２）QをAP'上に射影してMを求める。
（３）AP'上Mを中心にP'の対称点R'を求める。
（４）RP'の垂直２等分線とAP'の交点をB+とする。
（５）RR'の垂直２等分線とAP'の交点をB-とする。
なお、計算はフリーの数式処理ソフトMaxima-Primerによった。コマンド入力と結果出力を表３に示す。
（大変判りにくいと思いますが、解説は省略させていただきます。）
順接の場合 ［Xf(Ax,Ay)、Yf（Ax,Ay)］＝回転（順接（(Ax,Ay),９０度）、−９０度） とおけば、
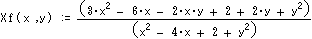
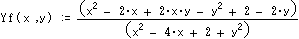
逆接の場合 ［Xr(Ax,Ay)、Yr（Ax,Ay)］＝回転（逆接（(Ax,Ay),９０度）、−９０度） とおけば、
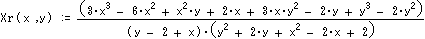
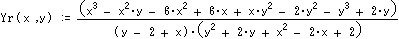
である。
さらに点Cは [ X*(X*(Ax,Ay),Y*(Ax,Ay)) , X*(X*(Ax,Ay),Y*(Ax,Ay)) ]=[X** (Ax,Ay) , Y** (Ax,Ay)]で表わせます。
ここで*はｆ又はｒであり、４通りあります。また４角形であるのでD点経由逆回りにも表わせ、
対称性から[X** (Ax,-Ay) , -Y** (Ax,-Ay)] であるといえます。 計算結果は以下です。
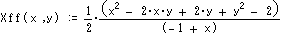
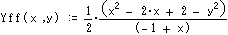
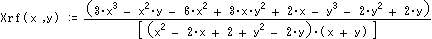
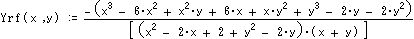
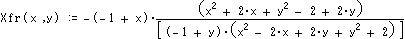
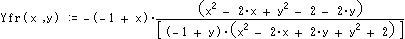
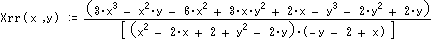
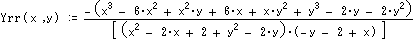
これらの式をB経由とD経由のCが等しいとして解けば題意を満たす［Ax,Ay］が得られる。
組み合わせは全部で１６通りあるが、環状に連結していることから
rr=rr , rr=rf , fr=rf , rf=rf , ff=fr , ff=ff
の６通りを考えればよい。
以下省略するが、分母を払って方程式を解くと
[Ax,Ay]=[±１、±１］、［0.0］、[3±√3、０］ という解が得られる。
一方、□PRQSは必ず□ABCDの内側にできるから、
[±１、±１］ 、［0.0］は解ではない。
また、[3-√3、０］は辺を見込む角度が１２０度以上であるからこれも解ではない。
よって、A=[3+√3、０］のみである。
また、この解をもたらす方程式の組み合わせは
rr=rr(正方形) と fr=rf（直角２等辺三角形）の２個である。
【感想】
美しい「モーリー定理」を数式処理で泥臭くまとめてしまい、本質が見えていないません。
そんな状態なので、任意のθに対して補題１が成立しているのは、かなり驚きの事実です。
幾何学的な何か腑に落ちる解釈方法があるのでしょうね。
３の倍数角形以外では、強に凸という条件を図形ＡＢＣ．．．につければ、正Ｎ角形に限られるように予想されます。
◆出題者のコメント
こんなに早く、解答をいただけるとは思っていませんでした。
【問題２】はまあ直角二等辺三角形の場合はご愛嬌として、PQRSが正方形ならABCDは正方形になります。
モーリーの定理と似たような解法で初等幾何的に解くことができます。
【発展問題2】に関しては完全な解答は持っていませんでした。
しかし、Y.M.Ojisanさんの解答は私の予想外なものでした。
私はN=４，５，６で成立してN≧７で成立しないと思っていましたから。
N=５の場合ですらこのような解があるとは。
