【問題1】
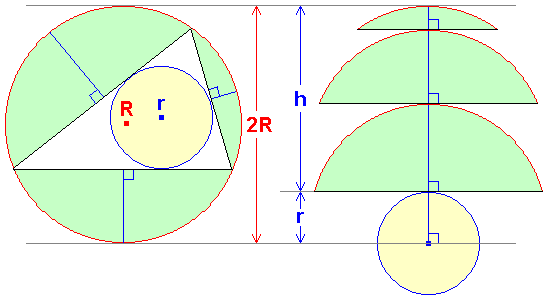
任意の三角形の外接円と内接円において、
外接円の半径をR、内接円の半径をr、3つの弓形の高さの合計をhとすると、
以下の関係式が成立することを示してください。
2R=r+h

【問題2】
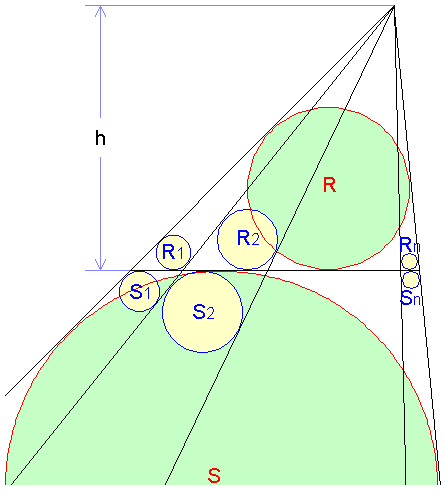
任意の三角形において、底辺を任意のn個に分け、図のようにn個の三角形に分割します。
元の三角形と分割された各三角形において、
内接円の半径を RおよびR1,R2,…,Rn とし、
底辺に接する傍接円の半径を SおよびS1,S2,…,Sn とすると、
以下の関係式が成立することを示してください。
ただし、hはすべての三角形の高さです。
| 1- | 2R h | =(1- | 2R1 h | ) | (1- | 2R2 h | )・・ | (1- | 2Rn h | ) |
| 1+ | 2S h | =(1+ | 2S1 h | ) | (1+ | 2S2 h | )・・ | (1+ | 2Sn h | ) |
【問題3】
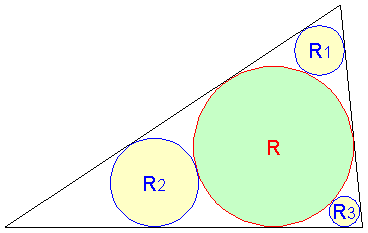
任意の三角形において、内接円の半径をR、
この内接円に外接し2辺に接する3つの円の半径を
R1,R2,R3とすると、
以下の関係式が成立することを示してください。
![]()
【問題4】
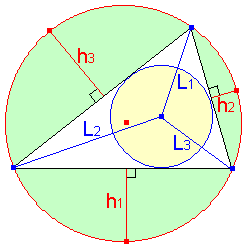
任意の三角形の外接円と内接円において、
内接円の中心から3頂点までの長さを L1,L2,L3 とし、
外接円と三角形の各辺とでできる3つの弓形の高さを h1,h2,h3 とすると、以下の関係式が成立することを示してください。
L1L2L3=8h1h2h3
【問題5】
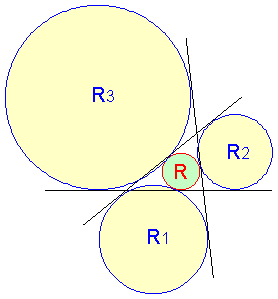
任意の三角形において、内接円の半径を R、この内接円に外接し2つの辺の延長線と接する3つの円の半径を
R1,R2,R3 とすると、以下の関係式が成立することを示してください。
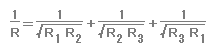
【問題6】
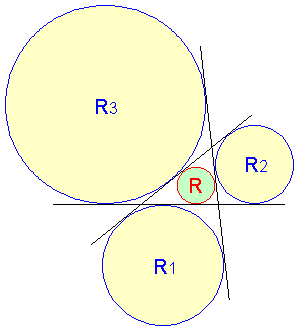
任意の三角形の内接円と傍接円において、内接円の半径を R、
3つの傍接円の半径を R1,R2,R3 とすると、以下の関係式が成立することを示してください。
| 1 R | = | 1 R1 | + | 1 R2 | + | 1 R3 |
【問題7】
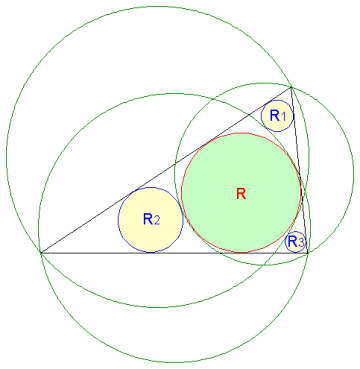
任意の三角形と、その三角形の内接円があります。
まず、内接円に外接し三角形の2頂点を通る3つの円を描きます。
次に、描いた2頂点を通る円に外接し三角形の2辺に接する3つの円を描きます。
3辺に接している内接円の半径を R、2辺に接している3つの円の半径を
R1,R2,R3 とすると、以下の関係式が成立することを示してください。
R= R1+R2+R3
解答用紙はこちらです。
【寄せられた解答】 【寄せられた解答その2】(NEW!!)
◆図形問題へもどる
 数学の部屋へもどる
数学の部屋へもどる