◆宮城県 アンパンマン さんからの解答。
【問題2】
n=2のとき、
| 1- | 2R h | =(1- | 2R1 h | ) | (1- | 2R2 h | )を証明します。 |
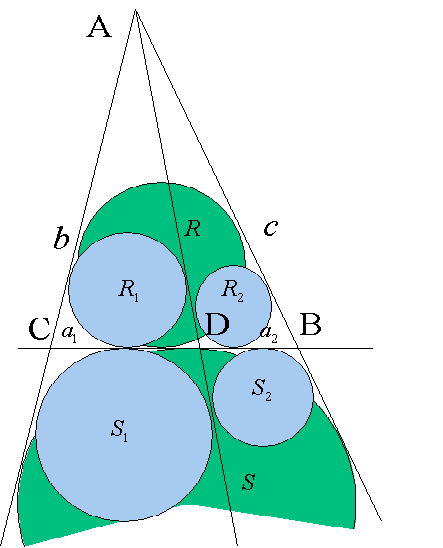
AB=c,AC=b,CD=a1,DB=a2,AD=dとします。
| d2+a1a2 = | c2 a1+b2 a2 a1+a2 |
がわかり、つまり
| (b+d)(c+d)+a1a2 a1(c+d)+a2(b+d) | = | b+c a1+a2 | です。 |
| x y | = | w z | から | x-y x+y | = | w-z w+z | が言えることより |
| (b+d)(c+d)+a1a2-a1(c+d)-a2(b+d) (b+d)(c+d)+a1a2+a1(c+d)+a2(b+d) |
| = | b+c-a1-a2 b+c+a1+a2 |
(b+d)(c+d)+a1a2-a1(c+d)-a2(b+d)
=(b+d-a1)(c+d-a2)
(b+d)(c+d)+a1a2+a1(c+d)+a2(b+d)
=(b+d+a1)(c+d+a2) より
| b+c-a1-a2 b+c+a1+a2 |
| = | b+d-a1 b+d+a1 |
・ | c+d-a2 c+d+a2 |
| 2R h | = | 2(a1+a2) b+c+a1+a2 | , |
| 2R1 h | = | 2a1 b+d+a1 | , |
| 2R2 h | = | 2a2 b+d+a2 | より |
| 1- | 2R h | =(1- | 2R1 h | ) | (1- | 2R2 h | )が成り立ちます。 |
n=2が成り立つことと帰納法より任意のnにも成立します。

また
| (1- | 2R h | )(1+ | 2S h | ) |
| =(1- | 2R1 h | )(1+ | 2S1 h | ) |
| =(1- | 2R2 h | )(1+ | 2S2 h | ) |
| =1 から |
| 1+ | 2S h | = | (1+ | 2S1 h | )(1+ | 2S2 h | ) あるいは |
| 1+ | 2S h | = | (1+ | 2S1 h | )(1+ | 2S2 h | )...(1+ | 2Sn h | ) |
◆愛知県 Y.M.Ojisan さんからの解答。
【問題2】
【定理1】
三角形ABCの辺BC上に点Dをとるとき、以下の関係がある。
| AD2= | AB2*CD+AC2*BD CD+BD | −BD*CD |
【定理2】
三角形ABCの内接円の半径をrとするとき、
| 三角形ABCの面積= | (AB+AC+BC)*r 2 |
【証明】
2分割の場合を証明すればよい。
n分割はその繰り返しである。
頂点をA 底辺をBC BC分割点をDとする。
定理2より
| 三角形ABCの面積= | BC*h 2 |
= | (AB+AC+BC)*R 2 |
| 1- | 2R h | = | AB+AC−BC AB+AC+BC |
同様に三角形ABD 三角形ACDを考えると
| 1- | 2R1 h | = | AB+AD−BD AB+AD+BD |
| 1- | 2R2 h | = | AC+AD−CD AC+AD+CD |
上2式の分母同士の掛け算を計算すると、BD+CD=BCなので、
(AB+AD+BD)*(AC+AD+CD)
=(AB+AC+BC)*AD+(AB+DB)*(AC+CD)+AD2
定理1によりAD2のみおきかえると、
(AB+AD+BD)*(AC+AD+CD)=(AB+AC+BC)*X
| ここで X=AD+ | AB*CD+AC*BD BC |
同様に分子同士は
(AB+AD−BD)*(AC+AD−CD)=(AB+AC−BC)*X
よって
| (1- | 2R1 h | ) | (1- | 2R2 h | )= | AB+AC−BC AB+AC+BC |
=1- | 2R h |
【問題1】
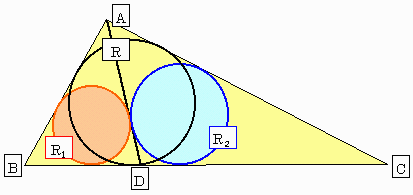
弦の半長を a,b,c 、 弦と外接円中心との距離を A,B,Cとします。
また弦に対向する三角形の角をαβγとします。
α+β+γ=π
すると円周角=中心角/2の関係から
(a,b,c)=R(sin(α), sin(β), sin(γ))
(A,B,C)=R(cos(α), cos(β), cos(γ))
一方、三角形の面積をQとすると(問題2の定理2等から)
Q=Aa+Bb+Cc=r(a+b+c)
また問題定義より、
h=(R−A)+(R−B)+(R−C)=3R−(A+B+C)
以上より
F=h+r−2R
| =R−(A+B+C)+ | Aa+Bb+Cc a+b+c |
| =R{1-(cos(α)+cos(β)+cos(γ))+ | sin(α)cos(α)+sin(β)cos(β)+sin(γ)cos(γ) sin(α)+sin(β)+sin(γ) | } |
分母を払います。
| F*(sin(α)+ sin(β)+ sin(γ)) R |
| ={sin(α)−sin(β)cos(γ)−sin(γ)cos(β)}+{初項同形式でα→β→γ循環}+{初項同形式でα←β←γ循環} |
ここに α=π―β−γ ないしその循環を代入して展開計算すると、
=0+0+0=0
Rが有限なら (sin(α)+ sin(β)+ sin(γ))>0であり
F=0 が成立。
すなわち 2R=h+r

【感想】
魅力的で綺麗な定理ですね。考えてみざるを得ませんでした。
2R(udius)をD(iameter)にするともう少し綺麗かも。
◆出題者のコメント。
解答ありがとうございます。
お二人とも正解です。
Y.M.Ojisan さんの【問題1】での証明は、一貫して循環性を崩さず、私が考えていた証明に比べて実にエレガントに感じます。
【問題2】の各三角形において、内接円でなく底辺に接する傍接円とすれば、なるほど確かにアンパンマン さんが示した関係式が成立しますね。
全然、気付きませんでした。
◆愛知県 Y.M.Ojisan さんからの解答。
【問題3】
Riに対応して角αiを下図のように定義します。i=1,2,3
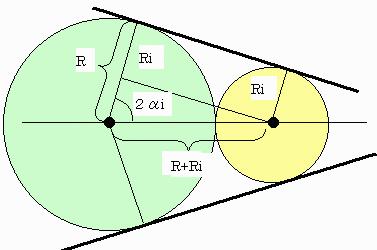
図より R=Ri+(R+Ri)cos(2αi) です。
三角関数公式を用いて変形すると、
| Ri R |
= | 1−cos(2αi) 1+cos(2αi) |
= | tan2(αi) |
従って、
| F= | R |
ここに
| α1 | = | π 2 |
− | α2 | − | α3 |
代入すれば(ほとんど公式ですが)
| F= | tan(α2)+tan(α3) tan(α2+α3) |
+tan (α2)tan(α3) |
よって
![]()
◆宮城県 アンパンマン さんからの解答。
![]()
と同じように
![]()
が成り立つことが言えます。
◆愛知県 Y.M.Ojisan さんからのコメント。
【問題3アンパンマンさんへコメント】
傍接円まで拡張できるのですね。なるほど。
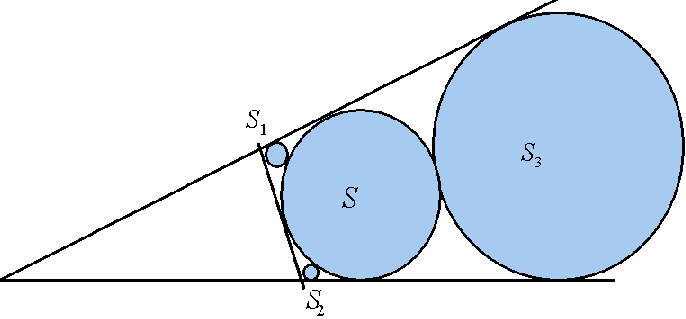
内接円の証明がそのまま適用できるよう、前回の解答の図を三角形の角を開放した図に修正しました。
◆出題者のコメント。
Y.M.Ojisan さん、早々に解答ありがとうございます。
実に鮮やかな証明だと思います。
それに、アンパンマン さんの洞察力には感服します。