『円の縁』

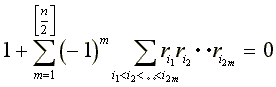
この問題は『円と三角形』の問題３を拡張した問題です。

【問題】

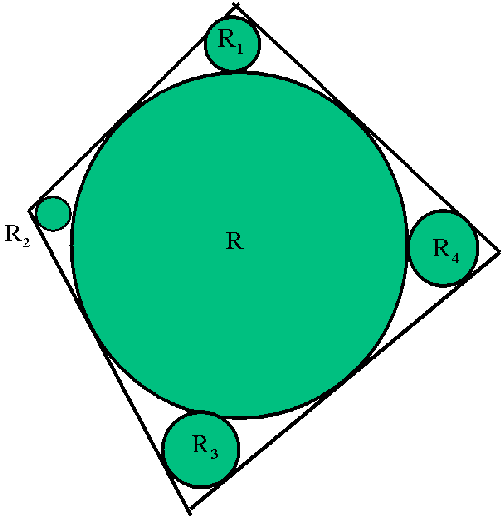
半径Rの円Oの外接n角形があります。
n角形の角と円Oでできたn個の内接円の半径を
R₁,R₂,...,R_nとします。
以下の関係式が成立することを示してください。

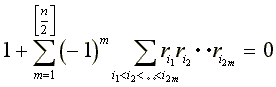
ただし

, i=1,2,...,n,

かつ[x]＝Floor関数です。

図の場合はn=4で、以下の関係式が成立します。

1-r1r2-r2r3-r3r4-r4r1-r1r3-r2r4+r1r2r3r4=0。

　解答用紙はこちらです。　【寄せられた解答】

　◆図形問題へもどる

　数学の部屋へもどる