『円の縁』解答

◆宮城県　甘泉法師 さんからの解答。

R1からさらに次々と頂点に向けて内接円を作ると
どんどん相似比 R1
R		＝r12 の小円ができる。

等比数列の和で円Rの中心から頂点１（内角をα1とする）までの距離があらわせるので
cosec( α1
2		)＝1+ ２r12
1-r12		 ＝ 1 + r12
1-r12

これから
r12＝(1-sin( α1
2		))／(1+sin( α1
2		 ))＝tan(π
4		- α1
4		)／tan(π
4		+ α1
4		 )

公式 tan(π
4		-A) tan( π
4		+ A)＝１を使い、
r1 ＝tan(π - α1
4		 )

公式
cos(A1+A2+...+An)=cosA1cosA2...cosAn(1-T2+T4-...)
Tmはn個の角の中からｍ個の角のtanの乗積をすべての組み合わせについてとったものの総和
引用：数学公式II 岩波全書初版183ページ

でAj＝π - αj
4		 とおくと左辺は cosπ
2		 ＝０なので
０＝1-T2+T4-...となり、証明すべき式になる。

【感想】

問題は公式を証明せよということと同じですね。

三角関数の加法定理の証明

（命題）

sin(A1+A2+...+An)
=cosA1cosA2...cosAn(T1-T3+.....)

cos(A1+A2+...+An)
=cosA1cosA2...cosAn(1-T2+T4-.....)

TkはtanA1,tanA2, ... ,tanAn からとったk個の積の、すべての組み合わせについての和。

（証明）

帰納法を使う。

Tkにはどのｎをかんがえているかのサフィックスをつけて区別する。
ｎ＝２のときは普通の加法定理から成り立つのが明らか

ｎのときに成り立つとしてn+1の場合を考える。

sin(A1+A2+...+An+An+1) 
=sin(A1+A2+...+An)cosAn+1+cos(A1+A2+...+An)sinAn+1
=cosA1cosA2...cosAncosAn+1(T1,n-T3,n+.....) + cosA1cosA2...cosAncosAn+1tanAn+1(1-T2,n+T4,n-....) 
=cosA1cosA2...cosAncosAn+1(T1,n+1-T3,n+1+.....)。
証明すべき関係式。 
cos(A1+A2+...+An+An+1) 
=cos(A1+A2+...+An)cosAn+1-sin(A1+A2+...+An)sinAn+1
=cosA1cosA2...cosAncosAn+1(1-T2,n+T4,n-....)-cosA1cosA2...cosAncosAn+1tanAn+1(T1,n-　T3,n+.....) 
=cosA1cosA2...cosAncosAn+1(1-T2,n+1+T4,n+1-....) 。
証明すべき関係式。

よって命題は証明された。

◆愛知県　Y.M.Ojisan さんからの解答。

「『円と三角形』問題３」で示されたように、
ｒK＝tan(αK)であり、この問題では下記に拡張される。
　（注：式(1)　〜(3')において総積/和の範囲K=１〜ｎは省略する。）

ΣαK＝π
２		 　----(1)

exp(i*α) exp(i*β)＝exp(i*(α＋β))　から下記等式(2)が導出される。

Π{１＋i*tan（αK）}＝exp(i*(ΣαK))/Π{cos（αK）} 　----(2)

ここに　（１）を代入すれば

Re[Π{１＋i*tan（αK）}] ＝０　-----(3)

すなわち

Re[Π{１＋i*ｒK }] ＝０　-----(3')

これを開けば 問題の下記式が得られる。
（総積/和の範囲表現を出題と若干変えた）

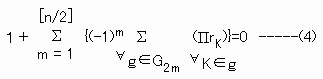
ここでG2mは　１〜ｎの整数の集合から異なる２ｍ個を選んだ組(ｇ)の集合である。
「（−１）m」は、i2から出ている。
初項「１」　は　ｍ＝０の場合を特出したもの。

◆出題者のコメント。

早々に解答ありがとうございます。２人とも正解です。
この関係式はn角形に限らず、円に接するn線分にも適用できます。

　『円の縁』へ

　数学の部屋へもどる