【問題1】
m角形、辺P1,P2,...,Pmで
PiとPjの角度=θij(m角形の内側の角度)。
Piの長さをLiとする。
次の式を証明してください。
| (Lk)2= |
Σ 1≦i≦m,i≠k | (Li)2-2 |
Σ 1≦i<j≦m,i,j≠k | Li*Lj*cos(θij) |
【問題2】
m多面体、面P1,P2,...,Pmで
PiとPjの角度=θij(m多面体の内側の角度)。
Piの面積をSiとする。
次の式を証明してください。
| (Sk)2= |
Σ 1≦i≦m,i≠k | (Si)2-2 |
Σ 1≦i<j≦m,i,j≠k | Si*Sj*cos(θij) |
【問題3】
(x1,x2,...,xn)∈Rn,
面 P1(a1,1*x1+a1,2*x2+...+a1,n*xn=b1),
面 P2(a2,1*x1+a2,2*x2+...+a2,n*xn=b2),
...,
面 Pm(am,1*x1+am,2*x2+...+am,n*xn=bm)
からn次元のm多面体をつくります。
面 Pi上のm多面体の面をQi, i=1,...,m。
Qiの面積をSi。
面Qiと面Qjの角度=θij; i,j∈{1,2,...,m}
(m多面体の内側の角度)とする。
次の式を証明してください。
| (Sk)2= |
Σ 1≦i≦m,i≠k | (Si)2-2 |
Σ 1≦i<j≦m,i,j≠k | Si*Sj*cos(θij) |
ここでn次元上の体積(S)とcos(θ)を次のように定義します。
ア)
n次元の(n+1)面体の頂点を
V1(c11,c12,...,c1n),
V2(c21,...,c2n),
...,
Vn+1(c(n+1)1,...,c(n+1)n)とすると,
V1V2...Vn+1の体積(S)は
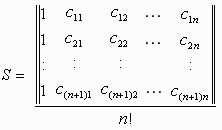
ここで ||x||=xの行列式の絶対値。
さらに、n次元の体積は(n+1)次元の面積と定義します。
イ)
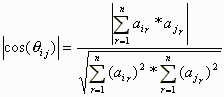
cos(θij)は正か負は、その内側の角度θijによります。
ちなみにm=n+1そしてPn+1以外はお互い直角、
つまりcos(θij)=0; i,j≠n+1,のとき 「n次元平方定理」が得られます。
そのとき
| (Sn+1)2= |
Σ 1≦i≦n | (Si)2 |
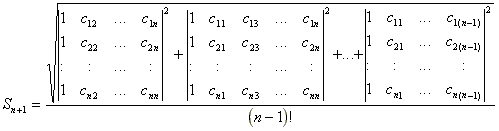
n次元のn角形(面積Sn+1)の頂点を
V1(c11,c12,...,c1n),
V2(c21,c22...,c2n),
...,
Vn(cn1,cn2,...,cnn)とします。
n次元平方定理をつかって面積 Sn+1をもとめると
◆図形問題へもどる
 数学の部屋へもどる
数学の部屋へもどる