【問題1】
どの4点も同一平面上にない6点があり、どの2点も赤か青の線分で結ばれている。
このとき、同色の3辺を持つ三角形が必ず存在する。
その理由を示せ。
【問題2】
7点があり、どの点も他の4点以上と直接線で結ばれている。
このとき、これらの線に沿って移動できるものとすると、
どの点からであっても、必ず他のすべての点を1度ずつ通って戻ってこれる。
その理由を示せ。
【問題3】
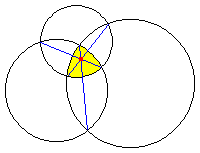
図のように、どの2円も2交点を持つように3円が重なっている。
(3円が重なるとは、図の黄色部分のような領域が存在することを意味する。)
このとき、各2円の2交点を結ぶ3本の線分は、必ず1点で交わる。
その理由を示せ。

【問題4】
先生がある8人の生徒に向かって、この(その8人の)中に友達は何人いるのか尋ねると、
8人の生徒はそれぞれ、
6人,6人,5人,4人,3人,2人,1人,1人 と答えた。
それを聞いた先生は、ちょっと考えてから「そんなことは絶対ありえない」と言った。
その理由を示せ。
ただし、AにとってBが友達なら、BにとってもAは必ず友達であるものとする。
【問題5】
各チームを各点とし、チーム間の試合の結果を勝ちチームの点から負けチームの点に矢印を書いて表すものとすると、
n(≧2)チームによる総当たり戦の結果には、矢印に従って進んでもn個の点すべてを1度ずつ通る道筋が必ず存在する。
その理由を示せ。
ただし、どの試合にも引き分けはないものとする。
以下、追加問題です。
【問題6】
どの3点も同一直線上にない、n個ずつの赤い点と青い点が同じ平面上にある。
このとき、どの2本も接しない両端点が赤と青のn本の線分が必ず引ける。
その理由を示せ。
【問題7】
2点間を結ぶ線を辺と呼ぶものとすると、同一平面上において、
n(≧3)個の点に存在できる交差しない辺の最多は(3nー6)本である。
その理由を示せ。
ただし、辺は曲線でもかまわないが、どの2点においても多くても1本とする。
◆図形問題へもどる
 数学の部屋へもどる
数学の部屋へもどる