『拡張中点連結定理』

　今回のテーマは中学校２年生で習う中点連結定理の拡張です。
中学生以上向きです。

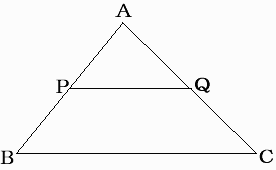
普通、中点連結定理といえば、 △ＡＢＣの２辺ＡＢ，ＡＣの中点をＰ，Ｑとし、ＰＱを結ぶ。 すると２ＰＱ＝ＢＣで、ＰＱとＢＣは平行になる。 というものをいいますが、次のように定理を拡張してはどうでしょうか。 ＜中点連結定理の拡張＞ △ＡＢＣの辺ＡＢ，ＡＣ上に点Ｐ，Ｑをとる。 このとき、 (1)　ＰはＡＢの中点 (2)　ＱはＡＣの中点 (3)　２ＰＱ＝ＢＣ (4)　ＰＱとＢＣは平行 という４つの条件のうち２つを満たせば、他の２つの条件も満たす。 「(1)(2)が成り立つならば、(3)(4)が成り立つ」というのが、普通の中点連結定理です。 （以後、簡単に「(1)(2) → (3)(4)」と書きます。） また、この逆、つまり「(3)(4) → (1)(2)」も成り立ちます。 実は、上の＜中点連結定理の拡張＞は正しくありません。 以下の問いに答えてください。 【問題１】 「(1)(4) → (2)(3)」は成り立つことを証明してください。 【問題２】 １の逆「(2)(3) → (1)(4)」が成り立たない例を挙げてください。 【問題３】 「(1)(3) → (2)(4)」は成り立つでしょうか。 １，２の結果から考えてください。 【問題４】 ３の逆「(2)(4) → (1)(3)」は成り立つでしょうか。 １，２の結果から考えてください。 【問題５】 「中点連結定理の拡張」を正しく書き直してください。

　解答用紙はこちらです。　【寄せられた解答】

　◆図形問題へもどる

　数学の部屋へもどる