『時計の針が作る面積 Part2』

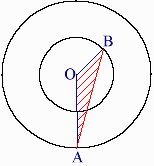
ｘｙ平面上に円x²+y²=1およびx²+y²=4をとる。
前者の半径を時計の短針、後者の半径を時計の長針とし、初期状態を0時0分とする。
長針が進んだ後にできる角度をθとし、短針は長針が一周すると一時間だけ進むものとする。

【問題１】

長針の先端をA、短針の先端をBとするとき、線分ABの長さをθを用いて表してください。

【問題２】

三角形ABOの面積Sをθを用いて表してください。

【問題３】

Sの最大値・最小値、およびそのときのθをk(=0,1,2,3…)で一般化して求めてください。

Ｐ．Ｓ

『時計の針が作る面積』の問題にも挑戦してみてください。

　◆方程式へもどる