『正方形の問題 Part２』

【問題１】

K先生はある生徒から以下のような問題を質問されました。

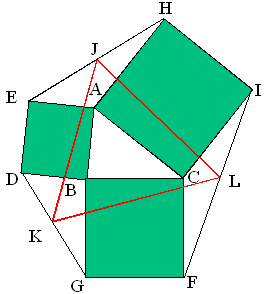
「三角形ABCの外側に正方形ABDE,正方形BCFG,正方形CAHIを図のように書きます。
EH,DG,FIの中点をそれぞれJ,K,Lとします。
この時三角形JKLは正三角形であることを示しなさい。」

K先生は座標を用いて証明しようとしましたが、上記の問題が成立しないことに気が付きました。
しかしながら、ある問題を考えつきました。

「上記で逆に三角形JKLが正三角形であるならば、三角形ABCは正三角形であると言えるでしょうか。」

これを考えてみてください。

【問題２】

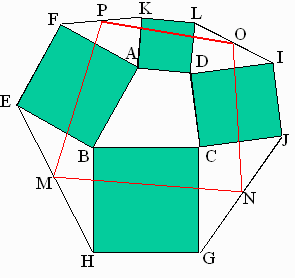
四角形ABCDの外側に正方形ABEF,正方形BCGH,正方形CDIJ,正方形DAKLを書き、EH,GJ,IL,KFの中点をそれぞれM,N,O,Pとします。
四角形MNOPが正方形の時、四角形ABCDは正方形であると言えるでしょうか。

PS．【問題２】の方が易しいと思います。できれば初等幾何学的な解法を募集します。

　解答用紙はこちらです。　【寄せられた解答】

　◆図形問題へもどる

　数学の部屋へもどる