当然、三角形は最大５個できます。
ただし三角形の個数は「重なり合う部分が（頂点以外に）ないもの」を数えます。
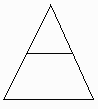例えば、この図では三角形は２個ではなく、１個と数えます。
【問題１】
星形五角形に２本の直線を付け加えて、三角形を１０個作ってください。
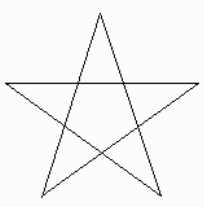この図に直線を書き込んで、メールで送ってくださると嬉しいです。
【問題２】
６本の直線を使って三角形は最大何個できるでしょうか。
【問題３】
問題１を発展させます。
７本の直線を使って三角形を１１個作ることはできるでしょうか。
◆問題２，３とも画像を送ってくださると嬉しいです。
以前の問題は難しそうなので、問題を改題します。
【問題４】
ｎ本の直線を使って、三角形を最大Ｓ個作ることができるとします。
| Ｓ≦［ | ｎ(ｎ−２) ３ | ］ |
ただしｎ本のうちのどの３本の直線をとっても１点で交わることはないとします。
［ ］はガウス記号（その中の数を越えない最大の整数）です。
【問題５】（超難問）
問題４で、３直線が１点で交わる時も、上の不等式は成り立つでしょうか。
【問題６】（超難問）
ｎ本の直線を使って、三角形を最大何個作ることができるでしょうか。
ただしｎ本のうちのどの３本の直線をとっても１点で交わることはないとします。
【注意】
問題５，６は私も解答を知りません。
【問題７】（追加問題）
東京都 建築家 さんからの問題です。
どの３直線も一点で交わらずどの２直線も平行でないとします。
| 直線に囲まれた有界な領域の数は | (n-1)(n-2) 2 | 個 |
それを囲む辺の数はn(n-2) 本
またどの三角形も隣あうことはない事に注意します。
| もし三角形の数が | n(n-2) 3 | 個あったとすると |
そしてある１本の直線について注目しますと
丁度(n-2)個の三角形に接していることになります。
そしてポイントはその三角形はその１本の直線を挟んで逆側に交互に現れます。
さてこのことを前提にして【追加問題】です。
n≡0,2(mod 6)となるようなｎに対して、三角形が
| ［ | ｎ(ｎ−２) ３ | ］個できることはないことを証明して下さい。 |
同値ですがガウス記号を外して、nが偶数の時に
| ｎ(ｎ−２) ３ | 個できることはありません。 |
これよりn=6の時に三角形が８個できないことが証明できます。
数学の部屋