◆上田 正次 さんからの解答。
斎藤 誠さんの解答を参考に、三角形の最大の求め方を発展・整理しました。
星型n角形が存在するとき、(n+1)本での三角形の数を最大にする方法は以下のいずれか。
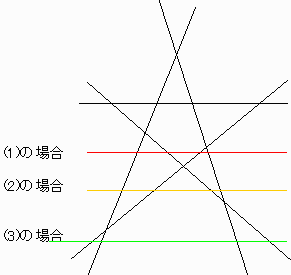
1.例として、星型5角形から始める場合
(1)五角形の内部に直線を引くと六角形に「変化」する。
(2)5角形の外側で且つ「出っ張り三角形」を通る直線を引く。
「出っ張り三角形」とは、星型多角形で多角形の辺の延長線で作られる三角形をいう。
(星型の星を作っている三角形である)
(3)出っ張り三角形の外側に「クロス三角形」を作るように直線を引く。
「クロス三角形」とは、出っ張り三角形が周囲に対して 交差した点より外側に出来る三角形をいう。
※(2)(3)を区分するために、(2)の場合の直線を内直線と呼ぶ。
(3)の場合の直線を外直線と呼ぶことにする。
※(3)の場合について考察したことが今回の発展ポイントである。

2.次に、(n+2) (n+3)本目を引く場合
効果的に三角形の個数をより多く作るには、星型多角形を取り囲む様に引けばよい。
(直線3本あれば取り囲める)
即ち、(n+1) (n+2) (n+3)本の3直線で星型多角形を取り囲む。
3.最後に、直線n本で作る三角形の最大個数は
星型(n-2)角形+2直線。
星型(n-1)角形+1直線。
星型n角形
のなかの最大になる場合を採用する。
(nが増えるとより複雑になるが)
以上から、n=3から始めて、最大個数を求めた場合を以下の資料に書いている。
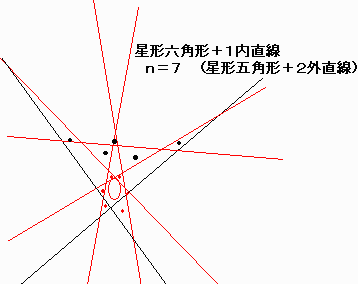
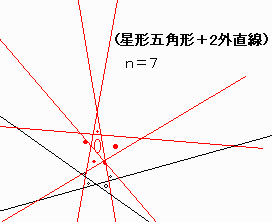
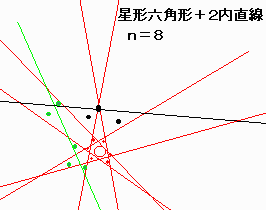
ここで、星型多角形の基になる多角形が移動していることが着目される。
資料の図形の場合、nを一つ増やす毎に、前の図形に 直線を一本追加している。
(但し、n=7の場合 出っ張り三角形を追加直線側に集めている。)
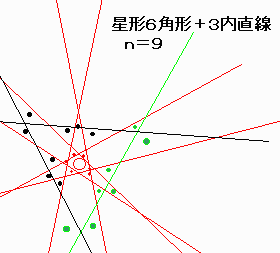
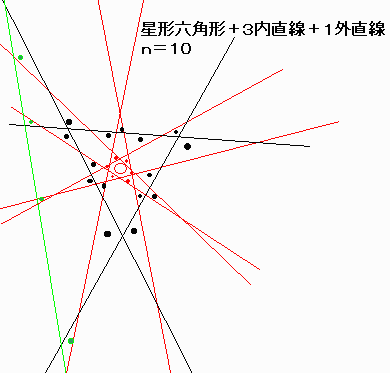
| n | 基になる多角形 | 内直線 | 外直線 | 最大の三角形数 |
| 3 | 3 | 0 | 0 | 1 |
| 4 | 4 | 0 | 0 | 2 |
| 5 | 5 | 0 | 0 | 5 |
| 6 | 5 | 0 | 1 | 7 |
| 7 | 6 | 1 | 0 | 11 |
| 8 | 6 | 2 | 0 | 14 |
| 9 | 6 | 3 | 0 | 21 |
| 10 | 6 | 3 | 1 | 25 |
n=11~13の場合は通称「バコさん」が投稿予定です。
◆バコ さんからの解答。
最初に最大個数を作るにあたって、四角形平面を考えておきます。
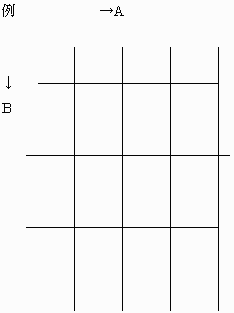
上記のように、成分を2つに分けておきます。
これは、3本以上の直線は1点では交わらないという条件より、成分は2つになります。
3本の直線が1点で交わる場合には、これは3方向に分かれます。
n本の直線が1点で交わる場合は、n方向に分けて考えます。
そして、分け方は
縦(横)n/2(偶数の場合)、n-1/2 or n+1/2(奇数の場合)、
横(縦)n/2(偶数の場合)、n+1/2 or n-1/2(奇数の場合)
となります。
そして、この四角形群の中でどちらか多いほうの(偶数の場合はどちらでも可)直線を使って最大交点を作ります。
(最大交点とはn(n-1)/2のことです)
これを利用して最大個数を作っていきます。
(この四角形の縦と横は上記に示してあるようなものでなくてもできます。
例えば、この場合だと縦2、横5というようにやっても最大個数は変わりません。
今回は考え易いようにこの図でやっています)
●次に、3本以上の直線が1点で交わることのない三角形の最大個数を考えるにあたって、
その交点の最大個数はn(n-1)/2個です。
そして、その1交点の隣を1本の直線が通るとそれは1個の三角形ができたことになります。
∠→⊿
そして三角形ができた反対側でも同じことが起こります。
(ここではその2直線の先は考慮に入れないものとします)

この図のように上下できるということです。
つまりは、ここでは2本の直線に挟まれた交点(3本以上の直線で交わらない)は2つの三角形(最大個数)を作るということです。
これを応用します。
そうすると、簡単に言えば交点を2直線で挟めば2つの三角形ができるということです。
さきほどの四角形群より、多いほうの直線で最大交点を作ります。
それを本数の少ないほうの直線で挟んでいきます。
すると2直線に囲まれる三角形は上記の例の四角形平面で考えると、
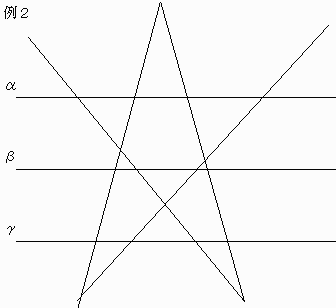
この図のようになります。
これは、四角形の個数/2の四角形が2つの三角形に変わっていると考えると、
四角形の個数/2×2で最終的にもとの四角形の個数になることが分かります。
(α、β、γの3直線に囲まれた三角形の最大個数)
最後に残りの3本ですが、答えを先に言うと実はこの例2の場合でいくと、横(α、β、γ)の最大個数は2個になります。
つまりは、4本での最大個数となるわけです。
もっと言うと、縦の直線4本(最大交点を作っているほうの直線群)を1本の直線とみなします。
そうすれば、それ1本+α+β+γ=計4本となり、
この最大個数+縦の4本直線の最大個数=例の本数でできる三角形での最大個数となります。
(この式をΓとしておきます)
この要領で作っていくと、この場合だけでなくn本の場合も、三角形の最大個数はn本で作られる四角形平面の四角形の個数と同じになります。
しかし、ここでちょっとした問題が起きます。
それは、ある決まった本数の場合は無視して良いのですが、ある本数の場合には上の式の通りに計算しても3本以上の直線が一点では、交わらない条件の最大個数は出て来ないということなのです。
これはどういうことかと言うと、
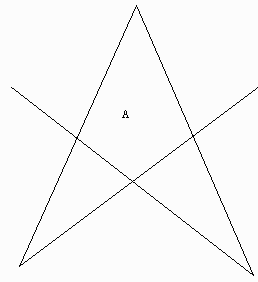
上記のような場合、さきほどの式(Γ)ではAの部分は三角形ができているはずなのですが、その下に交点があるため三角形ができていない。
このような場合には、ある決まった数を引かなければならないということです。
ある決まった数とは、縦の項(横の本数―1)が奇数の場合には
{n/2 or (n-1)/2 or (n+1)/2}}/2を引きます。
ただ、四角形群を作ったときに真中に四角形ができるような本数のときは、最大個数の作り方は2通りあります。
つまりは、4nの場合です。
4n本の場合(4n本とは、4、8,12,16・・・・本のことです)はn/4個の個数をさっきの式(Γ)の値から引かなければならなりません。
4n本の場合は出し方は先ほども言ったように、2通りあるのです。
(両方同じ答えになりますが)
そこで、ひとつは今まで通りのやり方で良いのですが、2つ目のやり方はちょっと違うので説明しておきます。
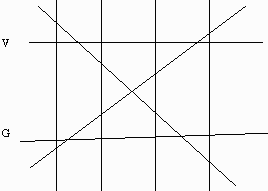
上の図の場合、VとGはこの先で交わるものとすれば、この場合だけで11個の三角形ができています。
(今までのやり方だと、この時点では10個なはずです)
このように、中心を通るか通らないかで多少やり方が違ってくるということです。
3本以上の直線の交点はもたないという条件の中では、今までのやり方とこのやり方とでは同じ値が出てきます。
(これは3本以上の直線の交点はもたないという条件の中での最大個数)
そして、今までの結果を分かり易く描くと、
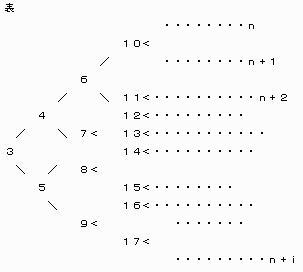
この数字はそれぞれ本数を示しています。
(3,4,5,6・・・・・n+i)本
つまりは、お互い偶数本と奇数本等個数を作り合いながら増えていくということです。
そして、これより2n+1本の最大個数の式と2n+2本の最大個数の式を求めてみました。
詳しい説明は長くなってしまうので省きますが、式だけを言っておきますと
2n+1本のときは
●4n-1/3 n=1,2,3,4、・・・・・
これは、さっきの表の一番上側と下側を示したものです。
そして、n本のときの作り方の判別方法も記載しておきます。
最初に偶数本での判別法を示します。
偶数本の場合2つの成分に分けたとき、どちらも同じ本数に分けます。
ここで、さきほどの例2より、N(偶数本)/2+1=(N+2)/2
+1は例2でいう「縦の直線4本(最大交点を作っているほうの直線群)を1本の直線とみなします」これを意味したものです。
これと同じ要領で奇数本のほうも作ると、(M(奇数本)+1)/2となります。
●この2つを使って、15本でかつどの3本をとっても1点で交わることはないという条件の最大個数を求めてみます。
15は奇数であるから、奇数本の式(上記の)に15を代入すると、8という数字が出てきます。
この調子で最後の3本に辿り着くまでやると
15→8→5→3
という順番で数字が出てきます。
これを利用して、15本になるまでを求めてみます。
最初はもちろん3=三角形は1つなので、5本の式はある式(R1)+1
次の8本では(R2)+(R1)+1
次の15本では(R3)+(R2)+(R1)+1となります。
ここで、Rとは『多いほうの直線の交点の最大個数-四角形の個数/2+四角形の個数+少ないほうの直線の最大個数=その本数の最大個数』という式になります。
しかし、4n個そして4C+3(C=2,3,4,5・・・)は、
Rから{n/2 or (n-1)/2 or (n+1)/2}}/2を引かなければなりません。
このようにして、組み合わせた式によってできていく個数も決まってくるのです。
本来はもっと単純に説明できるのかもしれませんが、このやり方が個人的に一番説明し易かったので。
式のほうも、もっとまとめることが可能なのかもしれませんが、こちらのほうでは重要になるような式の求め方と
2n+1本のときを求めてみました。
◆東京都 建築家 さんからの解答。
【問題4】
どの3つの直線も1点で交わらないとし、どの2つの直線も平行でないとする。
まず辺によって周りを囲まれた領域を有界な領域と呼ぶことにする。
有界な領域を囲む辺の数はn本の辺それぞれに対し両端の2半直線を除いた
(n-2)本となるので、有界な領域を囲む辺の数は全部でn(n-2)本。
またどの3直線も1点で交わらないので、隣り合う二つの領域が三角形同士ということはありえない。
| よって三角形の数は高々[ |
n(n-2) 3 | ]個となる。 |
【問題5】
まず、i本のどの3つも交わらない直線で平面を分割する時、
有界な領域を囲む辺の数をL[i]=i(i-2)とする。
今、1つの交点に3本以上の重複がある場合を考える。
j≧3の時、j本が交わる交点の数をk[j]とすると、
有界な領域を囲む辺の数は
n(n-2)-Σk[i]*L[i]
となる。
3本以上交わることによって隣り合った三角形の数をL'とすると、共有する辺の数に等しいのだが、 L'個の辺を共有する辺に重ねて付加すれば、共有する辺がないとしてみることができる。
(i-2)を交点に対して3本以上の重複度としてみると
高々 L'≦Σ3*(i-2)*k[i] なので、これを付加すると
| S[n]≦[ |
n(n-2)-Σk[i]*L[i]-Σ3*(i-2)*k[i] 3 | ] |
| =[ |
n(n-2)-Σ(n-3)(i-2)*k[i] 3 | ] |
| ≦[ |
n(n-2) 3 | ](∵n≧3) |
がいえる