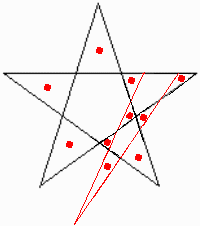
◆愛知県 重永 大介 さんからの解答。
【問題1】

【問題3】
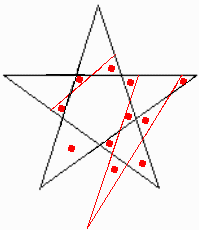
図の印を付けたところに三角形ができます。
問題2は、7個の三角形はできたのですが、もっと多くできそうなので送りませんでした。
【コメント】
見事、正解です。
問題2も、7個で正解です。
もしよろしければ、解答を送ってください。
◆愛知県 重永 大介 さんからの解答。
【問題2】
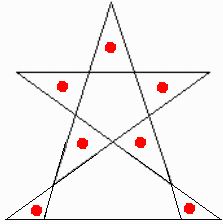
問題2の図はこのようになりました。
7個の三角形ができたのですが、まだこれが最大ということを示してないので不十分だと思います。
【コメント】
問題4の不等式を使えば、最大でも
6×4÷3=8個であることは、わかります。
たぶん8個はできないので、7個で正解だと思いますが、証明は難しいですね。
◆埼玉県 斉藤 誠 さんからの解答。
「問2、3、6の一部」
10本までの直線でできる三角形の最大数と思われる物(一部分)と、
| [ | n(n−2) 3 | ]、最大数、Nの対応表を作成しました。 |
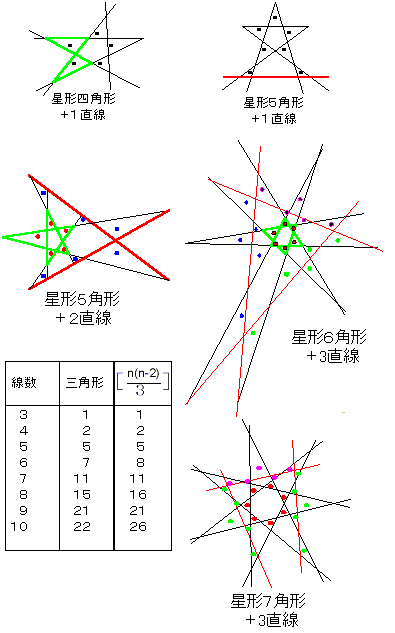
これを見ると、
| 奇数のときは[ | n(n−2) 3 | ]に等しくなりそうですが |
S(11)=33なので1個不足します
+1本で8個作るのも難しそう
【コメント】
この表は間違いなく正しいと思います。
| 奇数で[ | n(n−2) 3 | ]に等しくなるというのは、 |
◆北海道の高校生 なつみ&しずか さんからの解答。
【問題1】

上の図で、三角形は10個あります。
一つは小さくてわかりにくいですが・・・。
◆広島県 清川 育男 さんからのコメント。
【問題6】
数列サイトで検索してみました。
未解決の問題のようです。
斉藤さんの10本のときの個数が正しいとすれば新発見だと思います。
1983年以後の報告がありません。
<参考>
ID Number: A006066 (Formerly M1334)
0
Sequence: 0,0,1,2,5,7,11,15,21
Name: Maximum triangles formed from n lines.
References M. Gardner, Wheels, Life and Other Mathematical Amusements.
Freeman,NY, 1983, p. 171.
Keywords:nonn
Offset: 1
Author(s): njas
◆広島県 清川 育男 さんからの解答。
【問題4】
多角形の対角線の数を求めるときの考え方ではだめなのでしょうか?。
ある交わった直線2本があるとき、それにさらに交わって三角形が出来るとすれば、
他の直線は高々n−2本である。
したがって、n(n−2)本となるが、このことはどの3本でも言えるので3で割らなければならない。
出来る三角形は整数個であるから、求める三角形の個数は
| 高々[ | n(n−2) 3 | ]である。 |
したがって、
| S≦[ | n(n−2) 3 | ] |
◆保坂 さんからの解答。
【問題1】
