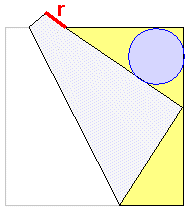
【問題1】
正方形の紙の左下の頂点が、図のように右側の辺に接するように任意に折り曲げる。
このとき右上にできる三角形の内接円の半径は、図の赤線rに等しいことを示せ。

【問題2】
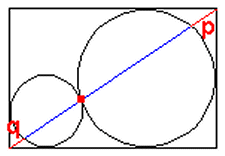
任意の大きさの2つの円が、図のように長方形の中にピッタリ納まっている。
このとき、2円の接点は長方形の対角線(図の青線)上にあることを示せ。
また、対角線の円外にある2つの部分の長さをそれぞれp,q(p≧q)とすると、対角線の全長はいくらか?
【問題3】
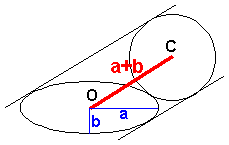
長軸と短軸の長さがそれぞれ2aと2bである楕円(中心O)に、任意の平行な2接線を引く。
これらの2接線に接し楕円に外接する円(中心C)を描くと、
常に OC=a+b であることを示せ。
【P・S】
鎖国であった江戸時代、各地の神社や仏閣には、数学の奉納絵馬(算額)が掲げられました。
その時代の算額に描かれた数学の問題や解法は、西洋数学とは独立して発展した和算独自のものですが、
特に幾何学の分野における算額には、感動させられるものが数多くあります。
(それ以来、神社や仏閣に算額を掲げる習慣が残ったそうです。)
出題の3問は、そんな算額の内で個人的に面白いと思った問題です。
◆図形問題へもどる
 数学の部屋へもどる
数学の部屋へもどる