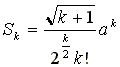
【問題】
n次元上の正(n+1)面体の各k次元面要素を(m+1)次元面に投影して、
(m+1)次元面(つまりm次元空間)に投影された部分の(k+1)次元面
(つまりk次元空間)の面積2の和を
正(n+1)面体の(k+1)次元面の面積2で割ると定数になります。
(n>m≧k≧0)
その定数をr(n,m,k)で表します。
要するに、正(n+1)面体のi番目の(k+1)次元面要素をP(k,i)とし、
P(k,i)のm次元面上の投影図の面積をQ(k,i)とすると
| n+1Ck+1 Σ i=1 | Q(k,i)2=r(n,m,k)(Sk)2。 |
Skは正(k+1)面体の体積と定義し、
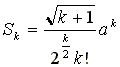
ここで、aは正(n+1)面体の2次元面要素(つまり線)の長さとします。
ちなみに、n+1Ck+1は正(n+1)面体の(k+1)次元面要素の数です
(『n-D parallel planes』問題のおまけのところを参考してください)。
では、次のことを証明してください。
| ア) r(n,k,k)= | n+1 k+1 | 。 |
| イ) r(n,m,k)=mCk r(n,k,k)=mCk | n+1 k+1 | 。 |
例えば、図1の場合:
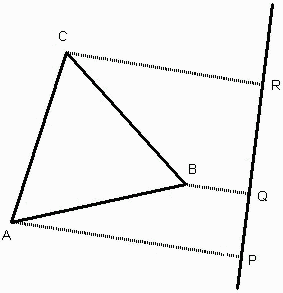
PQ2+QR2+RP2
=r(2,1,1)AB2
=3/2 (S1)2
=3/2 a2
図2の場合:
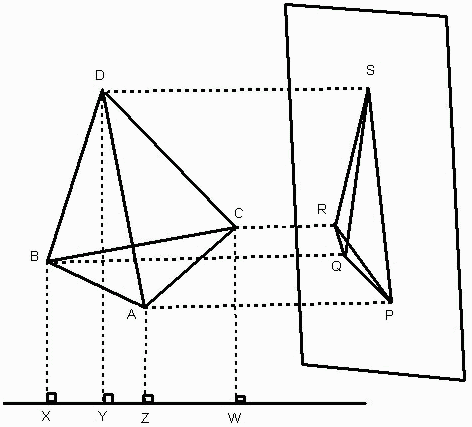
△PQR2+△PRS2+△QRS2+△PQS2
=r(3,2,2) (△ABC)2
=4/3 (S2)2
=1/4 a4
XY2+YZ2+ZX2+XW2+YW2+ZW2
=r(3,1,1)AB2
=2 (S1)2
=2a2
PQ2+QR2+RQ2+PS2+QS2+RS2
=r(3,2,1)AB2
=2C1 2(S1)2
=4a2。
必要ならば次のことを使ってください。
n次元上の正(n+1)面体の一つの頂点P0,P1,...,Pnは
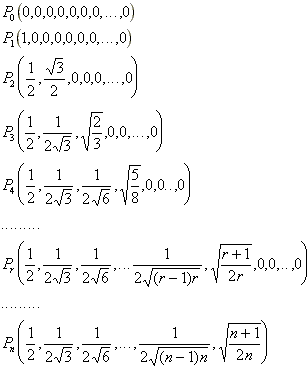
どの2点も1の距離で離れています。
解答用紙はこちらです。
◆図形問題へもどる
 数学の部屋へもどる
数学の部屋へもどる