『面積最大の四角形』

　今回のテーマは、面積が最大の四角形を見つけることです。
高校生以上向きです。

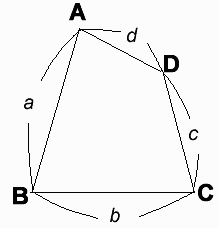
●新潟県　タカ３ さんからの追加問題。 【問題１】 周長一定の三角形のうち、面積が最大になるのは正三角形である事を証明せよ。 【問題２】 与えられた円に外接する三角形で、面積が最小になるのは正三角形である事を証明せよ。 (ヒントはヘロンの公式) 　 左図の四角形ＡＢＣＤの各辺の長さはそれぞれａ，ｂ，ｃ，ｄであるとします。 ただしａ，ｂ，ｃ，ｄは一定の長さです。 【問題３】 　この四角形の面積が最大になるのはどういう場合でしょうか。

　解答用紙はこちらです。　【寄せられた解答】

　◆図形問題へもどる

　数学の部屋へもどる