仧搶嫗搒丂俧俷俥倄丒榓恖偝傫偐傜偺夝摎丅
亂栤戣俁亃
傉偼偀丄偙偺栤戣偼壗傪媮傔偰嫃傞傫偩丠丠
壌丄崱丄悓偭偰嫃傞傫偩丅壗偑埆偄丠丠乮杮摉側傫偩丄偙傜両乯
偖傂偂丅柺愊嵟戝偺巐妏宍丠丠
傫側偺曈偺挿偝偺崌寁偑戝偒偔側傟偽柍尷戝偵奼嶶偡傞傢偄丅
嵟嬤偼柍尷戝偵廂懇偡傞傫偩偭偰丠
儚僔偺崰偼偦傫側榖偼側偐偭偨偧丅傑偁椙偄丅
偙偺栤戣偑栤戣偲偟偰惉傝棫偮偵偼乽堦掕偺奜廃傪帩偮巐妏宍偱乿嵟戝柺愊偵側傞偺偼丠 偲偄偆堄枴偩傠丠丠
傫偵傖傠両 堘偭偰偄偨傜媰偄偪傖偆偐傜側丅
傎傫偱傕偭偰丄偦傫側忦審偱偉丄傊偔偭丄奜妏傪帩偮巐妏宍偼丄巐妏丄偟偐偔丄偟偭偐偔丄幐奿丅
捈姶偩偗偳偋丄嵟戝偵側傞傢偗側偄偠傖傫丅
傫偠傖丄撪妏偩偗傪帩偮巐妏宍傪堦斒壔偟偰偉丄懳妏慄傪傂偄偰傒傛偆偐偭丄傂偔偭丅
偱偒偁偑偭偨係屄偺嶰妏宍傪峫偊傞偲丄滸暯偵側傞傎偳奜廃偵懳偟偰柺愊偺岠棪偑埆偄偠傖傫丅
傫偠傖惓嶰妏宍係屄傪廤傔傟偽嵟戝岠棪偐丠丄偰傫偺丅
偱傕偹偉惓嶰妏宍係屄傪傂偭偮偗傞偲傂偟宍丒丒丒暯峴巐曈宍偲傕備偆傛側偀丅
偙偄偮丄幬曈偺孹偒偺暘偩偗柺愊岠棪偑埆偄偠傖傫丅
傆傫偠傖丄係捈妏偺挿曽宍偼丠丒丒椬傝崌偆丒丒栚偑夢偭偰偒偨丒丒憗偄偲偙廔傢傜偣傛偭丅
椬傝崌偆曈偺挿偝偵嵎偑偁傞傎偳柺愊岠棪埆偄偠傖傫丅
偁傜丠僉乕儃乕僪偑偲傠偗偰傞丠丠
寢嬊惓曽宍偑嵟傕岠棪偄偄偺偩丅偙傜両埆偄偐両
偦偆尵偊偽丄傊偖偭丄奜廃偑堦掕偺応崌丄惓懡妏宍偑嵟傕柺愊偑峀偐偭偨傛偆側婰壇偑丒丒
傕偆巜愭偑丄摢偑丄懌偑丄俧倳倳倳丒丒丒丒丒
亂僐儊儞僩亃
丂傕偆偩偄傇俛倕倕倰偑傑傢偭偨偧丅
帺暘偱嶌偭偨俛倕倕倰偼傗偭傁傝偆傔偉側偀乕丄傂偔偭丅
愄丄廃堦掕偺帪偺嵟戝柺愊偺恾宍傕媮傔偨側偀乕丅
偦偆偄傗崱搙偼堘偆栤戣弌偟偨偭偗丅
倎丆倐丆們丆倓偼寛傑偭偨挿偝偩偐傜丄曄偊偨傜傑偢偄偢傜丅
妏搙偵偳傫側娭學偑偁偭偨傜丄嵟傕柺愊偑峀偄傫偩傠偆丠丠丠丠偲偄偆栤戣偱偉偡丅
仧搶嫗搒丂俧俷俥倄丒榓恖偝傫偐傜偺夝摎丅
亂栤戣俁亃
偁偼偭丄忀桘栤戣偐丅僜乕僗偐丄傕偆柪傢僱乕僘丅崱擔偼僔儔僼偩偤両乮偳偆偵偐乯
偊偊偲丄偲傝偁偊偢懳妏慄傪堷偄偰傒傛偭偐丅

懳妏慄俛俢傪俴侾偲偟偰傒傛偭丅
乮偮偄偱偵懳妏慄俙俠傪俴俀偲偟傛偆乯
傗傗偙偟偄偺偱慄暘俙俛丄俴侾丄俙俢偺挿偝傪倎丆俴侾丄倓偲偟傛偭偐丅
乮傑偨偮偄偱偵慄暘俛俠丄俠俢傪倐丆們偲偡傞偧乯
乮倎亄俴侾亄倓乯乛俀傪壖偵俰侾偲偡傞偲嶰妏宍俙俛俢偺柺愊偼岞幃偐傜
![]()
摨條偵慄暘俛俠丄俠俢丆俴侾偺挿偝傪倐丄們丄俴侾偲偟偰傒傛偭丅
乮倐亄們亄俴侾乯乛俀傪俰俀偲偡傞偲嶰妏宍俛俠俢偺柺愊偼岞幃偐傜
![]()
偲側傝側傜傓丄偐側丅
偙偙偱 倐亄們亜倎亄倓偺応崌傪峫偊傞偲偟偰倎亄倓亅俴侾亖俴倶偲偟偰傒傑偟傚偆偐丅
倎亄倓亖俴侾偺偲偒丄俰侾亖倎倓亅俴倶乛俀亖俴侾亄俴倶乛俀偵側傞偐傜
![]()
偲側傞偐側丠丠丠丠
偊偊偄両彂偄偰偄傞杮恖偑傢偗夝傜側偔側偭偰偒偨丅
梫偡傞偵懳妏慄偺峛抧乮偙偭偪乯偑挿偗傝傖壋抧乮偁偭偪乯偑抁偔側傞偵偩丅
倎亄倓亖俴侾偺偲偒偵俴侾偑嵟戝丄俴俀偑嵟彫丅乮倎亄倓亙亖倐亄們偺応崌乯
倎亄倐亖俴俀偺偲偒偵俴俀偑嵟戝丄俴侾偑嵟彫丅乮倎亄倐亙亖們亄倓偺応崌乯
偙傟偭偰巐妏宍偺嵟戝柺愊傪俴侾丆俴俀偺慻傒崌傢偣偺拞偐傜媮傔傞傗偮丅
悽娫條偑乽慄宍寁夋朄乿偲屇傫偱偄傞傗偮偐丠
乽傢偨偔偟丄傆偆偰傫偺俧俷俥倄偲敪巭傑偡偼暥宯偺弌恎偱偛偞偄傑偡乿
側傫偰偙偲偼尵偄栿偵偟傑偣傫偑丄慄宍寁夋朄偵怗傟偨帠偑側偄丅
傕偭偲僄儗僈儞僩側夝朄偼側偄傕偺偐丠
偍偍両偁傝偦偆偩丅愭偺岞幃偵愽傫偱偄傞偠傖側偄偺偐丠
懳妏慄俙俠偺挿偝傪俙俤亖俴侾丄俤俠亖俴俀丄俛俢偺挿偝傪俛俤亖俴俁丆俤俢亖俴係偲嵞掕媊偟偰傒傛偆丅
嘆巐妏宍偺曈偺挿偝倎丆倐丆們丆倓偼曄偊傜傟側偄丅
嘇懳妏慄偺挿偝偼懳峈偡傞曈偺挿偝偺崌寁偵埶懚偟偰曄壔壜擻丅
嘊嶰妏宍俙俤俢偺柺愊偼曈倓偑堦掕側偺偱俴侾丄俴係偺愊偵斾椺偡傞丅
嘋嶰妏宍俛俤俠偺柺愊傕曈倐偑堦掕側偺偱俴俀丆俴俁偺愊偵斾椺偡傞丅
嘍嶰妏宍俙俛俤丄俠俢俤傕摨條偵俴侾丆俴俁 俴俀丄俴係偺愊偵斾椺偡傞丅
寢榑偲偟偰巐妏宍偺俀偮偺懳妏慄偺挿偝偺愊偑嵟戝偺偲偒丄柺愊傕嵟戝偵側傞丅
乮偳偆傕偦偺偲偒俀偮偺懳妏慄偺榓傕嵟戝偵側傞傜偟偄丅怺偔峫偊偰偄側偄偗傟偳乯
巹偑悓偭傁傜偭偰夦摎傪婑偣偨擔乮擔梛擔乯丄偁傞埻岄偺夛偵嶲壛偟偨擔偱偟偨丅
嶲壛幰偺拞偵偼仏挿扟愳屲榊巵傗仏彫椦惓媊夛挿傕嫃傑偟偨丅
仏挿扟愳屲榊巵丗尰戙僆僙儘偺憂巒幰丅傕偲僆僙儘柤恖丅埻岄傾儅屲抜奿乮嫮偄屲抜乯
仏彫椦惓媊夛挿丗惻棟巑偑偮偔傞埻岄僋儔僽偺慡擔杮尰栶夛挿丅埻岄僾儘偺彫椦妎乮尦婝惞乯丄愮庻丄側偳僾儘俁孼掜偺妜晝丅
妝偟偔岄傪懪偭偰妝偟偔堸傫偱丄嫇偘嬪偺壥偰偁偺傛偆側夦摎偑偱偒偁偑傝傑偟偨丅
乮偍偍偭丄抪偢偐偟偄乯
僔儔僼偺崱擔傕夦摎偵曄傢傝偁傝傑偣傫偑丄戣堄偩偗偼惓偟偔偮偐傫偩傛偆偱偡丅
>傊偔偭丄奜妏傪帩偮巐妏宍偼丄巐妏丄偟偐偔丄偟偭偐偔丄幐奿丅>
偍偍偭丄奜妏傪帩偨側偄懡妏宍偲偼丠丠偦傫側偺側偄傛丅
尵偄偨偐偭偨偺偼懡暘丒丒丒偁傟丠扨岅偑弌偰偙側偄丅悓偭偰偄偰傕僔儔僼偱傕曄傢傝側偄偐丅
傎傜丄巐妏宍側傜丄傗偠傝偺傛偆偵撪妏偺堦偮偑俷倴倕倰侾俉侽搙偺懡妏宍丅
偩傟偐嫵偊偰壓偝偄丅偦傫側懡妏宍偺憤徧偲偦偺妏搙丅
亂僐儊儞僩亃
丂奜妏傪帩偨側偄巐妏宍仺墯巐妏宍側傫偰偄偆傛偆偱偡傛丅
偱偒偨傜妏搙偺娭學丄堦敪偱昞偣傞偲偐偭偙偄偄側偀丅
仧搶嫗搒丂M.Y 偝傫偐傜偺夝摎丅
亂栤戣俁亃
偙偺栤戣偼丄傒傫側悓偭暐偄側偑傜傗傞偺偐丅
偒偭偲悓偭暐偄尷掕栤戣偩側偀丅
傛乕偟丄偍傟傕堸傫偱峫偊傞偲偡傞偐両
偛偔偭丄偛偔偭丄偛偔偭丄........
傉偼乕丄傂偂乕乕乕乕乕乕両
傗偭傁帺暘偱偡偭偰嶌偭偨傝傫偛100%僕儏乕僗偼偆傑偄偹偉丅傂偭偔丅
側偵側偵丠 偙偺傕傫偩偄丄僐儊儞僩傪傛傓偲丄傂偭偔丅
乽妏搙偵偳傫側娭學偑偁偭偨傜丄嵟傕柺愊偑峀偄傫偩傠偆丠丠丠丠乿
乽偱偒偨傜妏搙偺娭學丄堦敪偱昞偣傞偲偐偭偙偄偄側偀丅乿
偩偭偰偉丠 傂偭偔丅
傂偭傂偭傂偭傂丄偙乕傫側偙偲彂偄偪傖乕丄偩傔偩傛乕丅傂偭偔丅
偙傝傖偀摎偊偼丄懳妏偺妏偺榓偑180搙偭偰偙偲偱丄巐妏宍偑墌偵撪愙偡傞偲偒偩側偀丅偒偭偲偦乕偵偪偑偄偁傞傔偉丅傂偭偔丅
傫偠傖丄懳妏慄偺1偮傪曄悢偵偲偭偰峫偊傞偲丄偒偄偭偲丄廂廍偑偮偐側偔側傞側丅傂偭偔丅
傫偠傖丄偙偙偼妏傪曄悢偵偟偰傗偭偐偀丅傂偭偔丅
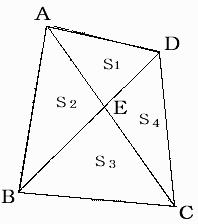
傑偢偼丄巐妏宍ABCD偺柺愊傪S丄妏B傪x搙丄妏D傪y搙偲偟偰S傪媮傔偰傒傫傋丅
| 俽亖 | 侾 俀 | 倎倐sin(x)亄 | 侾 俀 |
們倓sin(y) |
丂|俙俠|2
亖倎2亄倐2亅俀倎倐cos(x)
亖們2亄倓2亅俀們倓cos(y)
傫側丄姶偠傗側丅偙傟偱y傪徚嫀偟偰S傪旝暘偡傝傖丄偍偟傑偄偩....偲偄偄偨偄偲偙傠偩偗偳丄柺搢偩偟丄偦傫側偒偨側偔側偭偨幃側傫偰偩傟傕尒偨偔偹乕偧丅
偙偆偄偆忦審晅偒嬌抣栤戣傪夝偔偲偒傖丄傗偭傁丄Lagrange偺枹掕忔悢朄偩傠丅
側傫偱丄偙傫側曋棙側曽朄傪崅峑惗偵偼嫵偊側偄傫偩丅
偁偺偲偒乮丠乯偼丄偙偆偄偆栤戣傪夝偔偲偒偼嬯楯偟偨偤.....偆偭偆偭偆偭丅
偍偭偲丄愭傪懕偗偵傖丅偲傝偁偊偢怴偟偄娭悢傪T丄曄悢傪z偲偱傕偟偰
丂俿(x,y,z)
亖俽(x,y)+z(倎2+倐2-俀倎倐cos(x)-們2-倓2+俀們倓cos(y))
| 亖 | 1 2 | ab sin(x) | + | 1 2 |
cd sin(y)+z(a2+b2-俀ab cos(x)-c2-d2+2cd cos(y)) |
T傪x丄y丄z偱曃旝暘偟偰丄=0偵偡傞偲
| dT dx | 亖 | 侾 俀 |
ab cos(x)+2zab sin(x)=0 |
| dT dy | 亖 | 侾 俀 |
cd cos(y)-2zcd sin(x)=0 |
| dT dz | 亖 | a2+b2-2ab cos(x)-c2+d2+2cd cos(y)=0 |
乮忦審幃偦偺傕偺乯
忋偺2偮偺幃偐傜x偲y偺娭學傪媮傔傞偲
| 倸亖 | 1 4 | cot(x)亖- | 1 4 | cot(y) |
tan(x)=-tan(y)
倶亄倷亖侾俉侽
偍偍丄傗偭傁梊憐捠傝偨偭偩丅
嵟屻偺幃偼x偲y傪嬶懱揑偵a丄b丄c丄d傪巊偭偰昞偡偨傔偺傕傫偩偐傜丄巊傢側偔偰傕栤戣側偐傠偆丅
偊丄側偵側偵丄偙傟偼丄偨偩嬌抣乮掆棷抣乯傪媮傔偨偩偗偱嵟戝偐偳偆偐傢偐傜側偄偭偰丠
偦傟偵嵶偐偄偲偙傠偱徹柧偑偸偗偰傞偭偰丠丠
偍偭偲丄偩偄傇悓偄乮丠乯偑夞偭偰偒偨側偀乕丄傕偆愢柧偡傞偺傕柺搢偩丅
尒偨栚傕柧傜偐側偙偲偩偟丅偪傖傫偲偟偨愢柧偼丄偟傜傆偵栠偭偨師偺婡夛偲偄偆偙偲偱....Zzzzzzz....
乮拲丗偨傇傫丄偙偺師偼側偄乯
亂僐儊儞僩亃
丂偆丄撉傫偱偄傞巹傕傑偨崱擔傕悓偭偰偄傞側偀丅
嵟嬤丄堸傑偢偵偼偄傜傟側偄傫偱偡傛丅偮傜偄偭偡丅
偟偐偟偙偺夝摎偼慛傗偐偩側偁偀丒丒丒丒
墌偵撪愙偡傞巐妏宍偩偭偨傜俷俲偲偄偆傢偗偐丅
仧佢俛亄佢俢亖侾俉侽搙偱偁傞巐妏宍偑懚嵼偡傞偙偲偺徹柧丅
乮侾乯倎亄倐亝們亄倓 偐偮倎亄倓亝倐亄們偺応崌丅
佢俛亖侾俉侽搙偵側偭偨応崌丄偮傑傝巐妏宍俙俛俠俢偑仮俙俠俢偵側偭偨応崌偼
佢俛亄佢俢亜侾俉侽搙丅乮恾傾乯
堦曽丄佢俙亖侾俉侽搙丄偮傑傝巐妏宍俙俛俠俢偑仮俛俠俢偵側偭偨応崌偼
佢俛亄佢俢亙侾俉侽搙丅乮恾僂乯
慜幰偐傜屻幰傑偱丄巐妏宍俙俛俠俢傪楢懕揑偵曄宍偡傟偽丄
佢俛亄佢俢傕楢懕揑偵曄壔偟丄拞娫抣偺掕棟傛傝彮側偔偲傕堦偮偼
佢俛亄佢俢亖侾俉侽搙偱偁傞巐妏宍偑懚嵼偡傞丅乮恾僀乯
乮俀乯倎亄倐亝們亄倓 偐偮倎亄倓亞倐亄們偺応崌丅
乮俁乯倎亄倐亞們亄倓 偐偮倎亄倓亝倐亄們偺応崌丅
乮係乯倎亄倐亞們亄倓 偐偮倎亄倓亞倐亄們偺応崌丅
偵偮偄偰傕摨條丅
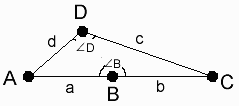
(傾)佢俛亄佢俢亜侾俉侽搙丅
丂丂丂伀
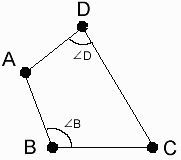
(僀)佢俛亄佢俢亖侾俉侽搙丅
丂丂丂伀
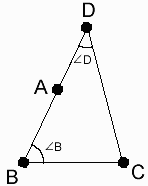
(僂)佢俛亄佢俢亙侾俉侽搙
仧堬忛導丂怴抾偺巕 偝傫偐傜偺夝摎丅
亂栤戣俁亃
巐妏宍偺柺愊傪 S, 傑偨 佢B = 兛丆佢D = 兝丆AC = x 偲偡傞偲
x2=a2+b2-2ab cos(兛)= c2+d2-2cd cos(兝)
偺忦審偺傕偲偵丆
| S = | 1 2 | ab sin兛 + | 1 2 | ab sin兝 |
偑嵟戝偲側傞偲偒丆x, 兛, 兝 偑偳偆側傞偐傪峫偊傟偽傛偄丅
丂偄傑 x 幉忋偵俁揰 E(a2 + b2, 0), F(c2 + d2, 0), P(x2, 0) 傪丆
傑偨 P 傪捠傞 x 幉偺悅慄忋偵恾侾偺傛偆偵
GE = 2ab, HF = 2cd 偲側傞揰 G, H 傪偲傝丆
佢GEP = 兛丆佢HFP = 兾-兝 偲偡傞偲
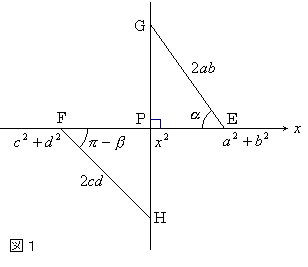
EP = a2+ b2- x2= 2ab cos兛
PF = x2- c2- d2= 2cd cos(兾-兝)
偱偁傝
| S = | 1 4 | {2ab sin兛 + 2cd sin(兾-兝)} = | 1 4 | ( GP + HP ) 乧 (拲) |
偲側傞丅
傛偭偰丆P 傪堏摦偟偨偲偒丆GH 偑嵟戝偲側傞偺偼偳偆偄偆応崌偐傪峫偊傟偽傛偄丅
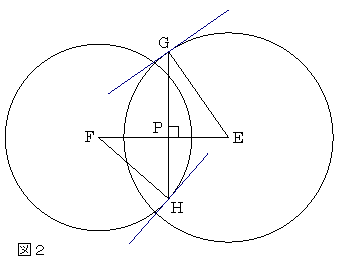
丂恾俀偵偍偄偰丆GP 偲 HP 偺憹尭偑僶儔儞僗偡傞偲偙傠偑嵟戝偩偐傜
(偪傚偭偲偄偄壛尭偐側 乧 (^^! 偍彆偗傪! )
G, H 偵偍偗傞墌 E, F 偺愙慄偺孹偒偑堦抳偡傞丆
偡側傢偪 GE, HF 偑暯峴偲側傞偺偑媮傔傞応崌丆
偟偨偑偭偰 兛=兾-兝丂傛傝丂兛+兝=兾
| 傑偨丂x2= | cd(a2+b2) + ab(c2+d2) ab + cd | 偲側傞丅 |
(拲)丂僿儘儞偺柺愊岞幃偐傜傕師幃偑惉傝棫偮丅
![]()
仧搶嫗搒丂愄偲偭偨媙暱 偝傫偐傜偺夝摎丅
亂栤戣俁亃
埲壓偺傾僀僨傿傾偼丄偦偺愄丄旝愊暘偺島媊偺侾夞栚偵乽偮偐傒乿偲偟偰暦偄偨暔偱偡丅
偙偺栤戣偺夝摎偲偟偰偼斀懃側偺偱偡偑丄偳偆偐戝栚偵尒偰偔偩偝偄丅
亙徹柧亜
傑偢丄栤戣偺巐妏宍ABCD 偑丄墌偵撪愙偟偰偄傞忬懺偺恾宍傪峫偊傑偡丅
偙偙偱丄墌廃偺挿偝偼丄 屖AB丄屖BC丄屖CD丄屖DA 偺係偮偺榓偱丄墌偺柺愊偼丄巐妏宍ABCD偲丄屖偲尫偱嫴傑傟偨晹暘係偮偺柺愊偺榓偵側偭偰偄傞帠偵拲堄偟傑偡丅
傕偟丄偙偺巐妏宍偑丄偝傜偵柺愊偺戝偒側暿偺宍 A'B'C'D' 偲偄偆宍偵側偭偨偲偟傑偡丅
偙偺巐妏宍A'B'C'D'偺奺曈偵丄愭掱偺屖AB丄屖BC丄屖CD丄屖DA 傪偔偭偮偗偨恾宍傪峫偊傞偲丄
恾宍偺廃偺挿偝偼丄屖AB丄屖BC丄屖CD丄屖DA 偺係偮偺榓偱丄
傑偨丄恾宍偺柺愊偼丄巐妏宍A'B'C'D'偲丄愭掱偺屖偲尫偱嫴傑傟偨晹暘係偮偺榓偵側傝傑偡丅
偮傑傝丄偙偺恾宍偼丄廃偺挿偝偼墌偲摨偠偱丄撪晹偺柺愊偑墌傛傝戝偒偔側偭偰偄傞偺偱偡丅
偙偆偄偆帠偼丄偁傝摼側偄乮両乯偺偱丄墌偵撪愙偟偰偄傞忬懺偑丄巐妏宍偺柺愊嵟戝偱偁傞帠偑帵偣傑偡丅