『空洞美術館定理』

今、任意の多角形の形（凸でなくともよい）をした美術館に防犯カメラを設置しようと思います。
その美術館の中にいくつかの多角形の空洞(穴)があります。
カメラは視線を遮る壁がない限り、３６０度全ての方向を監視することができます。

できるだけ少ない台数のカメラを設置して、死角を作ることなく監視できるようにしたいのです。

美術館の辺数は(穴の辺数を含めて)nとします。
穴の数をmとします。

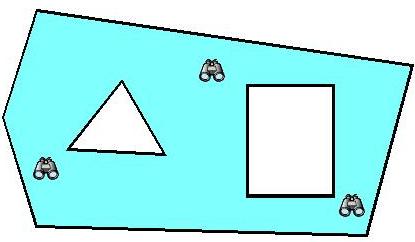
例えば、図の場合はn=12,m=2,カメラが3台必要です。

【問題１】

どんな形であろうとも防犯カメラが
［ n+3-m
3 ］台あれば、十分です。 (m≧1)
このことを証明してください。

ただし［　］はガウス記号（その数を超えない最大の整数）であるとします。

【問題２】

ちょうど［ n+3-m
3 ］台 (m≧1)必要になるような
空洞多角形の例を作ってください。