『ノミのジャンプ』

　今回のテーマは点の集まりでできる図形の面積に関する問題です。
はじめに次の問題を考えてみてください。

猫が３匹、１辺が１ｍの正三角形の頂点の位置にそれぞれいる。 この三角形の中にノミが１匹いた。 ノミは、その場の雰囲気で３匹の猫の中から１匹を選び、その猫めがけてジャンプしている。 ところが、いつも目測を誤るために、目標とする猫までの半分の距離しか跳ねない。 でも一生懸命、猫に近づこうとジャンプを繰り返した。 さて、ノミは猫にめでたく到達することができるだろうか。 また、ノミが着地することができた場所は三角形のどの部分か。 またその面積を求めよ。

◆それでは、実際に実験してみましょう。

＜ソフトウェアの使い方について＞

1. まずPolyで何角形にするかとratioでノミの跳ねる倍率を指定する。

2. 初期状態では三角形で倍率０．５（半分まで跳ぶ）である。

3. Startボタンでノミがジャンプを開始する。（最大20000回まで）
   赤の玉がノミ、黄色の点がノミの着地した点である。

4. Stopボタンでノミはジャンプを終える。

5. スクロールバーのSlowとFastでスピードを調節できる。

6. 角の数や倍率を変えて図形の変化を見てください。

　さて、それでは本当の問題です。

　図のように、一辺２０ｃｍの正三角形から、順に辺の長さが半分であるような正三角形を取り除いていく操作を繰り返します。

最初

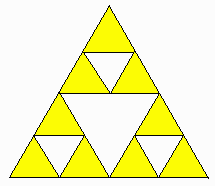１回目

２回目

【問題１】

　２回目、３回目、４回目の操作の後の黄色い部分の面積の和を求めてください。
中学校２年生以下の人は、最初の正三角形の面積は１７３ｃｍ²として計算してください。

【問題２】

　黄色い正三角形が２１８７個できるのは、何回目の操作の後ですか。

【問題３】

　この操作を無限に繰り返していくと、黄色い部分の面積の和はどうなるでしょうか。

　◆解答用紙はこちらです。　【寄せられた解答】

Ｐ．Ｓ

　この問題を「２１世紀への学校数学の展望」に執筆された山形大学教育学部　守屋誠司先生より、中学生に対してのカオスゲームをベースにしたフラクタルの指導実践の指導案等を送っていただきました。
先生のご好意に感謝いたします。

　◆図形問題へもどる

　数学の部屋へもどる