『円環の面積』

　今度は面積の問題がテーマです。

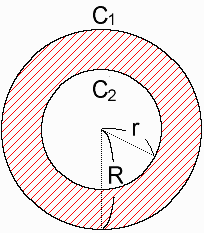
＜円環領域に含まれる多角形＞ ２つの同心円 半径Ｒの円Ｃ1 、半径ｒの円Ｃ2 がある。 ただし、Ｒ＞ｒとする。 【問題１】 Ｃ1 に内接し、かつ、Ｃ2 に外接する三角形が存在するとき、この三角形はどんな三角形ですか。 【問題２】 Ｃ1 に内接し、かつ、Ｃ2 に外接する三角形が存在するとき、 Ｒ：ｒを求めてください。 【問題３】 Ｃ1 に内接し、かつ、Ｃ2 に外接する三角形が存在するとき、 Ｃ1 とＣ2 に囲まれた円環部分の面積を求めてください。 【問題４】 Ｃ1 とＣ2 の半径が分からなくても、円環部分の面積を求める方法があります。 半径以外の、１ヵ所の長さをはかって面積を求める方法を考えてください。 【問題５】 問１〜３の「三角形」を「四角形」に変えると答えはどうなるでしょう。

　解答用紙はこちらです。　【寄せられた解答】

　◆図形問題へもどる

　数学の部屋へもどる