 ・r となる。
・r となる。◆石川県 平田 和弘 さんからの解答。
(問題1)
それぞれの円の中心は三角形の内心と外心で一致すのは三角形が正三角形のときなので
正三角形
(問題2)
中心Oから正三角形の頂点A,B,Cに対して線を引き、OAと内側の円が交わる点をDとする。
Dより内側の円の半径rでAC上に点をとりこれをEとする。
△ODEは正三角形なので∠ODE=60
よって∠ADE=120°となり∠ADE=∠AOC
よってDE//OC なので△ADE∽△AOC
AD:AO=AE:AC=r:R
∠AOC=120°、∠AOE=60°より
∠COE=60°
△AOEと△COEにおいて
OBは共通、
OA=OC、
∠AOE=∠COE
なので△AOE≡△COE
よってAE=EC
従って
r:R=AE:AC=AE:(AE+EC)=1:2
(問題3)
上記2より求める面積は
π・R2-π・r2
=π・(2r)2-π・r2
=3π・r2
(問題4)
∠OAE=30°、∠AOE=60°より
∠OEA=90°なので△AOEは直角三角形となる。
正三角形の1辺の長さをLとすると、問題2より
AB=L/2、OE=r、OA=2rなので三平方の定理より
L/2= ・r となる。
・r となる。
即ちr=L/(2・ )
)
従って問題3より
3π・r2
=3π・{L/(2・ )}2
)}2
=3/20・π・L2
正三角形の1辺の長さ(L)がわかれば、
3/20・π・L2 で求められる。
(問題5)
1.
四角形は正方形
2.
四角形の頂点をA,B,C,Dとして円の中心OからABに対して垂線をおろして交点をEとし、OからADに対して垂線をおろして交点をFとする。
OE=OF、OAは共通で直角三角形の合同条件より
△AOE≡△AOF
よって∠OAE=∠OAF=45°、
また∠AOE=∠AOF=45°となるので
平行四辺形AEOFについて
AE//OF、AF//OEかつ∠EAF=90°、
∠EOF=90°かつOE=OF=rなので
平行四辺形AEOFは正方形となる。
AE=r
△AOEに三平方の定理を適用して、
r:R=1:
3.
π・R2-π・r2
=π・( r)2-π・r2
r)2-π・r2
=π・r2
4.
△AOE≡△BOEなので、
正方形の1辺の長さをLとすると、
L/2:r=1:1
よって r=L/2
従って
π・r2
=π・(L/2)2
=1/4・π・L2
正方形の1辺の長さ(L)がわかれば、
1/4・π・L2 で求められる。
◆東京都 鳳 奥人 さんからの解答。
【問題1】
この三角形の頂点を下図の通りD,E,Fとし、C2とDE, EF, FDの接点をそれぞれG,H,Iとする。
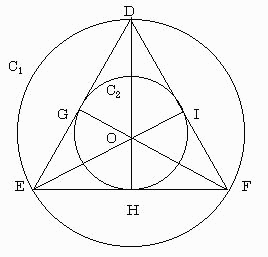
また、C1・C2の中心をOとする。
このとき、OD=OE=OF=R, OG=OH=OI=r となる。
またDE⊥OG、EF⊥OH、FD⊥OIである。
したがって、直角三角形の斜辺と他の一辺がそれぞれ等しいので
△ODG≡△OEG≡△OEH≡△OFH≡△OFI≡△ODI
これにより
∠ODG=∠OEG=∠OEH=∠OFH=∠OFI=∠ODI(=30°)
したがって
∠EDF=∠DEF=∠DFE(=60°)
よって、この三角形は正三角形である。
【問題2】
R:r=OD:OG=2:1
【問題3】
問題2よりR=2rであるから
円環部分の面積はπ(2r)2−πr2=3πr2
【問題5】
問題1と同様の考え方をすれば、この四角形が正方形であることは明白。
R:r=![]() r:1、
r:1、
すなわちR=![]() rとなるので
rとなるので
円環部分の面積は
π(![]() r)2−πr2=πr2
r)2−πr2=πr2
◆東京都の中学校3年生 もやし さんからの解答。
【問題4】
円C2の接線をひき、接点をT,接線と円C1との交点をA,Bとします。
すると、線分AT(BT)の長さの二乗は、
三平方の定理から、R2−r2となる。
求めたい面積はπ(R2−r2)なので、線分AT(BT)の長さをはかり、それを二乗してπ倍すればよい。
複数のドーナツ型があって、その大きさを比べるには、線分AT(BT)の長さをはかるだけでよい、という のを以前学校の授業でやりました。結構たのしかったです。
◆埼玉県 mist さんからの解答。
【問題1】
正三角形
問題3→問題2の順で解く。
正三角形と円C2の接する点は、正三角形の辺の中点となる。
正三角形の3辺の中点を結ぶと、大きさが等しい4つの小さな正三角形ができる。
真ん中の小さな三角形は円C2に内接する。
一方で、元の大きい正三角形は円C1に内接する。
面積の比が
大きい正三角形:小さい正三角形=4:1
だから、それらの正三角形に外接する円の面積の比も
円C1:円C2=4:1
円C2+円環=円C1から
円環の面積
=円C1−円C2
=(4−1)×円C2
=3πr2 ……問題3の答え
半径については
円C1:円C2=R2:r2=4:1から
R2=4r2
R=2r
R:r=2:1 ……問題2の答え