n0=1
『Arctangent問題』の中に、私の知らなかった（言うまでも無いか）面白い関係が有りましたので、これを種に変奏曲を作成しました。
全部同じ問題『ディオファントスの方程式』問題4 の変形に帰着できますが、別の方法があるかもしれません。
２次方程式と簡単な整数論をベースにとける問題ですから、中高生にもできると思います。
ヒント出しすぎかな？
【基本形】
（１）下記方程式を満足する自然数m ,nの組が無限に存在することを証明せよ。
１＋ｍ2＝２ｎ2
（２）条件を満たす全ての自然数ｎを小さいほうから並べた数列を
nI とするとき下記が成立することを証明せよ。
n0=1
【図形問題風】
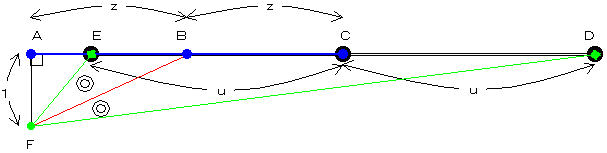
一直線上に点ＡＢＣ および点ＥＣＤがそれぞれ等間隔で並んでいます。
その長さをそれぞれz,uとします。
また点Ｆは点Ａおよび直線から距離１の点とします。
（１）線分ＦＢが角ＥＦＤの角度の２等分線であるような自然数z,uの組み合わせは、無限に存在することを証明せよ。
（２）条件を満たす全ての自然数ｎを小さいほうから並べた数列を
ｚI とするときこの数列の漸化式を見つけよ。
ｚ0=２ とする。
【整数論風】
（１）連続する２自然数の積の２倍が連続する２自然数の積である自然数m ,nの組が無限に存在することを証明せよ。
ｍ（ｍ＋１）＝２ｎ（ｎ＋１）
（２）条件を満たす全ての自然数ｎを小さいほうから並べた数列を
nI とするときこの数列の漸化式を見つけよ。
n0=２ とする。
【数論風】
に非常に近い有理数を下記条件を満足するｆと定義する。
（１）条件を満足するｆが無限に存在することを証明せよ。
（２）条件を満たす全ての有理数ｆを小さいほうから並べた数列を
ｆI とするときこの数列の漸化式を見つけよ。
ｆ0=１／１ とする。
【数値計算法風】
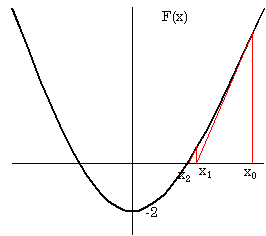
非線形の方程式F(x)=0を数値的に解く場合、ニュートン・ラプソン法は非常に有効な手段です。
方法は下図のように、接線との交点を求めながら反復計算で求めます。
具体的に Ｆ（ｘ）＝ｘ2−２ を用いてを求めてみます。
ニュートン・ラプソン法の欠点は 初期値を適切に選定しないと別の解の
（この場合は−）に収束することです。
ここでは初期値を x0=1.5 とします。
ｄＦ／ｄｘ＝２ｘ なので、反復計算式は下記です。
(2)は計算量を減らした式で、計算機にもよりますが、
割り算一回の計算時間＋少しです。
xi+1 = xi −(xi2-2)/2xi ―――――(1)
＝0.5 xi+1/xi ―――――(2)
を求める数値計算法は他にもいくらでもあります。
下記はそのひとつです。
(4)式は(2)式と同程度の計算時間です。
yi+1 =(4+3yi )/(3+2yi ) ―――――(3)
＝1.5−0.25/(1.5+yi ) ―――――(4)
下記問題の答えから (4)の方法はニュートン・ラプソン法に比べ計算時間がかかるが、初期値が自由であることが分かります。
＜問題＞
（１）
(4)式はに収束するが
−には y0=−を除き 収束しないことを証明せよ。
（２）
yI =ｍ/ｎ ： 既約分数 で表記した場合
ｍ2=2ｎ2+1 であることを示せ。
（３）
y0=ｘ0=1.5から始めた場合
数列 xiは数列 yiの部分数列であることを示せ。
（４）
数列 xiがI回の反復計算で所定の精度に達したとき,
数列 yiが同じ精度に達する反復計算回数をIの関数で表せ。
（おまけ）
が「一夜一夜にひとみ頃」と分かっているので、
初期値1.5と出来ましたが，数値解を求める場合、一般的にはもっと大雑把にしか分かっていません。
さて、初期値が −１０〜１０の間から一様な確率で出発する場合に
(2)(4)をうまく混ぜて使って、早く確実にに適当な精度でたどりつく戦略を考えてください。
if文などの部分の計算時間は無視して(2)と(4)の使用回数で判定するとします。
なお、問題の設定が曖昧であり、最小値に近ければよいので、いわゆる正解はありません。
if文を組み合わせて計算するのは反則です。
◆方程式へもどる
数学の部屋へもどる