『Arctangent』

【準備】

与えられた実数xに対して、

(*) tanθ=x

を満たす実数θをxの逆正接(arctangent)といい、
arctan xで表します。

tanは周期πの周期関数ですから、θはπの整数倍の自由度があります。
そこで、(*)を満たす実数θのうち

-π/2＜θ＜π/2であるものをxの逆正接の主値といい、
Arctan xで表します。

このときArctanは、tanの定義域を
区間(-π/2,π/2)に制限したものの逆関数になります。

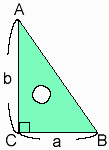
図形的に言えば、Arctan(b/a)は、
BC=a, AC=b, ∠C=π/2である直角三角形ABCの∠Bを意味します。

以上の準備の下、以下の問題(のうち少なくとも一つ)に答えてください。

【問題１】

整数x,y,z (z>0)が方程式

(1)　Arctan(1/x)+Arctan(1/y)=Arctan(1/z)

を満たすための必要十分条件は

　z²+1=uv, x=z+u, y=z+v

となる整数u,vが存在することであることを証明せよ。

【問題２】

整数x,y,z (0＜x＜|y|, z＞0)が方程式

(2)　Arctan(1/x)+Arctan(1/y)=2Arctan(1/z)

を満たすための必要十分条件を求めよ。

【問題２の変更】・・・詳細は【寄せられた解答】をご覧下さい。

問題２を以下のように改めます。

定義.

正の整数aに対して，整数列(u_n(a)), (v_n(a)) (n∈Z)を次のように定義する。

u_n(a)＋v_n(a)√d＝(a＋√d)ⁿ (n∈Z)

ただし，d＝a²＋1とする。

このとき，次の問題に挑戦してみてください。

【問題２】

正の整数x, y, z (x＜y)が方程式

Arctan(1/x)＋Arctan(1/y)＝2Arctan(1/z)

を満たすための必要十分条件は，ある正の整数aおよびnが存在して

x＝u_2n-1(a), y＝u_2n+1(a), z＝v_2n(a)

と表されることであり，また方程式

Arctan(1/x)－Arctan(1/y)＝2Arctan(1/z)

を満たすための必要十分条件は，ある正の整数nが存在して

x＝u_2n-1(1), y＝u_2n+1(1), z＝u_2n(1)

と表されることであることを示せ。

【問題３】

方程式

(3)　Arctan(1/x)+Arctan(1/y)=3Arctan(1/z)

を満たす整数x,y,zは存在しないことを証明せよ。

【問題４】

方程式

(4)　Arctan(1/x)+Arctan(1/y)=4Arctan(1/z)

を満たす整数x,y,zをすべて求めよ。