仧帬夑導丂堦暯偪傖傫 偝傫偐傜偺夝摎丅
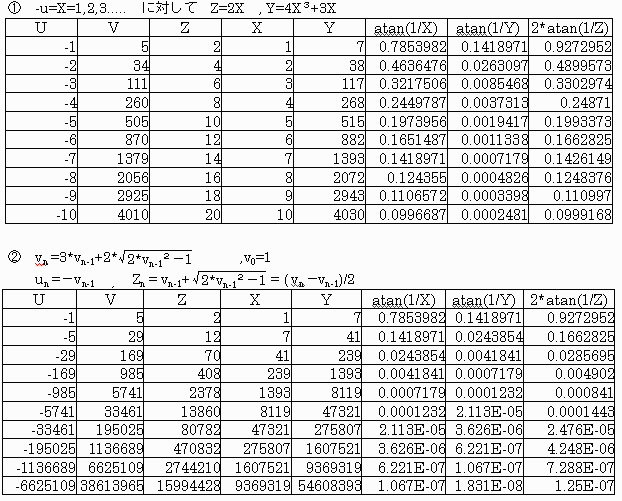
亂栤戣侾亃
| arctan( | 1 x | )亄arctan( |
1 y | )=arctan( | 1 z | ) 乧仏 |
仏偵偍偄偰椉曈偺惓愙傪偲傟偽丄壛朄掕棟傪揔梡偟偰丄
| 倶亄倷 倶倷亅侾 | 亖 |
1 倸 | 丂乧仈 |
傪摼傞丅
廬偭偰
| 倸亖 | 倶倷亅侾 倶亄倷 |
亪
| 倶亅倸亖 | 倶2亄侾 倶亄倷 |
| 倷亅倸亖 | 倷2亄侾 倶亄倷 |
偙傟傜傪偦傟偧傟倳丆倴偲偍偗偽丄
倸2亄侾亖倳倴丂偑惉棫偡傞丅
徹柧傪媡偵偨偳傞偙偲偵傛偭偰媡傕惉棫偡傞丅
仧晉嶳導丂N.C 偝傫偐傜偺僐儊儞僩丅
亂栤戣俀亃
夝摎偱偼側偄偺偱偡偑丆丏丏丏
(倶亄倷)偼俀倸偺攞悢偵側傞偙偲偑娙扨偵徹柧偱偒傑偡丅
偦偙偱丄倸偑4000埲壓偺応崌傪慡偰媮傔丄
| x+y 2z | 偺抣偵傛偭偰暘椶偟偰傒傑偟偨丅 |
婯懃偑偁傝偦偆偱敾傜偢丄庛傝傑偡丅
| x+y 2z | 亖亅侾偺偲偒 |
| x+y 2z | 亖俀偺偲偒 |
(x,y,z)=( 1, 7, 2)
(x,y,z)=( 7, 41, 12)
(x,y,z)=( 41, 239, 70)
(x,y,z)=( 239,1393, 408)
(x,y,z)=(1393,8119,2378)
| x+y 2z | 亖俆偺偲偒 |
(x,y,z)=( 2, 38, 4)
(x,y,z)=( 38, 682, 72)
(x,y,z)=(682,12238,1292)
| x+y 2z | 亖侾侽偺偲偒 |
(x,y,z)=( 3, 117, 6)
(x,y,z)=(117,4443,228)
| x+y 2z | 亖侾俈偺偲偒 |
(x,y,z)=( 4, 268, 8)
(x,y,z)=(268,17684,528)
埲壓棯丅
嶲峫傑偱偵丄倸偑係侽侽侽埲壓偺応崌傪媮傔傞廫恑俛俙俽俬俠梡偺僾儘僌儔儉丅
OPTION ARITHMETIC RATIONAL
function add(x,y)
let add=(x*y-1)/(x+y)
end function
for z=1 to 4000
let z2=add(z,z)
for x=1 to z-1
let y=add(z2,-x)
if 1=DENOM(y) then
print (x+y)/(2*z),"(x,y,z)=(";x;",";y;",";z;")"
end if
next x
next z
END仧垽抦導丂Y.M.Ojisan 偝傫偐傜偺夝摎
亂弨旛亃
cos(n兤)+i*sin(n兤)=(cos兤+i*sin兤)n -----(1)
傛傝 tan兤=1/Z偲偍偗偽丂(偨偩偟丂Z亗侽)
tan(2兤)=2Z/(Z2-1) -----(2)
tan(3兤)=(3Z2-1)/(Z3-3Z) -----(3)
tan(4兤)=(4Z3-4Z)/(Z4-6Z2+1) -----(4)
傑偨丄岞幃
tan(a+b) = (tan(a)+tan(b))/(1-tan(a)*tan(b)) -----(5)
栤戣偺幃偺嵍曈偼tan傪偲傞偲丄(5)偵傛傝
嵍曈亖(1/x+1/y)/(1-1/xy)=(x+y)/(xy-1) ----(6)
偨偩偟丄戣堄傛傝丂xy亗侽
傑偨丄arctan丂偼婏娭悢偱偁傞偺偱丄
Z亜0丂偲偟偰傕栤戣偲偟偰堦斒惈偼幐傢側偄丅
亂栤戣俀亃
Arctan(1/x)+Arctan(1/y)=2Arctan(1/z)丂丂丂-----(2-1)
Z=1偺偲偒塃曈偼 兾/2偱偁傞偑丂嵍曈偺嵟戝偼
x=y=1偺偲偒兾/2偱偁偭偰丄
偙傟偼 x亙|y|丂忦審偵崌傢側偄丅
傛偭偰丄俀亝Z丂偲偟偰傛偄丅
堦曽丂0亙x亙|y|偺忦審偱偁傞偑丄
嘆 0亙x亙y偺応崌 x亗y偺忦審偵抲偒偐偊偰傕x y偼懳徧側偺偱堦斒惈傪幐傢側偄丅
傑偨 z亜0側偺偱x亜0偺忦審傕偱傞丅
嘇 0亙x亙-y偺応崌偼丂z>侽偺忦審偐傜弌偰偔傞偺偱昁梫側偄丅
偡側傢偪丄晅懷忦審傪
俀亝Z丂偍傛傃丂x亗y 偱偁傞惍悢倶丄倷丄倸偲偟偰傕摍壙偱偁傞丅
(2)偲(6)傪乮2-1乯偵揔梡偡傞偲丄
(x+y)/(xy-1)=2Z/(Z2-1)
俀亝Z 偱偁傞偺偱 (Z2-1)亗侽
傑偨丄xy=1丂側傞惍悢倷,x亜0偼丄
倶亖倷亖侾偱偁傝
忦審丂x亗y偵斀偡傞丅
傛偭偰丄(xy-1)亗侽
埲忋傛傝椉曈偵
(Z2-1)(xy-1)傪偐偗偰傕丄摍壙偱偁傞丅懄偪
(Z2-1)*(x+y)-2Z*(xy-1)=0 ------(2-2)
偙偙偱栤戣侾摨條偵
x=Z+u y=Z+v 偲偍偗偽丂u,v偼惍悢偱
u亗v丂偱側偗傟偽側傜側偄丅
(2-2)偵戙擖偟惍棟偡傞偲丄
(Z2+1)*(u+v)+uv*2Z =0 ------(2-3)
(2-3)偼丂uv=0偺偲偒 u=v=0側傞夝傪傕偮偑
忦審丂u亗v丂偵斀偟偰偄傞丅
傛偭偰丄uv亗0側傞忦審偑昁梫偱偁傞偑丄
(2-3)傪壓婰偺傛偆偵彂偒姺偊傞偙偲偵傛傝
帺慠偵丂uv亗0偺忦審偑偮偔丅
2Z/(Z2+1) + (u+v)/uv = 0 ------(2-4)
偡側傢偪丄丂(2-4)傪枮懌偡傞丂惍悢丂u,v,Z偑懚嵼偡傞丅
偨偩偟丄俀亝Z
昁梫忦審徹柧姰椆
師偵丂俀亝Z丂偺偲偒丄(2-4)傪枮懌偡傞惍悢 z,u,v偑懚嵼偟偨偲偡傞丅
偙偺偲偒丂(2-4)偺摫弌夁掱偐傜丂(2-1)偼惉棫偡傞丅
偨偩偟丄u亗v偱柍偗傟偽側傜側偄偑
u=v=P丗惍悢偺偲偒丂幃(2-4)偼
丂P亖Z+1/Z
偲曄宍偝傟 俀亝Z丂Z:惍悢 側偺偱丂P偼惍悢偱偼側偄丅
傛偭偰丄u亗v偺忦審偼晄梫偱偁傞丅
懄偪廫暘忦審偱偁傞偙偲偑徹柧偝傟偨丅
亂栤戣俀摎偊亃
2Z/(Z2+1) + (u+v)/uv = 0丂傪枮懌偡傞惍悢
丂俀亝Z丆u丆v偑懚嵼偡傞偙偲丅
亂栤戣俀姶憐亃
堦墳栤戣偵夝摎偟偨偲巚偄傑偡偑丄偙傟偱姰惉側偺偐晄埨偱偡丅
偲偄偆偺偼丄偙偺幃偐傜偡偖偵偼夝偑尒偮偐傜側偄偐傜偱偡丅
師偺俀宯楍偺夝傪敪尒偱偒傑偟偨偑丄偦傟埲奜偵傕偁傝偦偆偱偡丅

亂栤戣俁亃
Arctan(1/x)+Arctan(1/y)=俁Arctan(1/z)丂-----(3-1)
Z=1偺偲偒塃曈偼 俁兾/係偱偁傞偑丂
嵍曈偺嵟戝偼 x=y=1偺偲偒俀兾/係偱偁偭偰丄惉棫偟側偄丅
傛偭偰丄俀亝Z丂偲偟偰傛偄丅
傑偨丄(3-1)偐傜 彮側偔偲傕x,y偺壗傟偐偼惓偐偮倅枹枮偱柍偗傟偽側傜偢丆
Z亜x亜0丂偲偡傞丅
偙偺偲偒 |y|亞x偱偁傞偲偟偰傛偄丅
乮3乯偲乮6乯傪乮3-1乯偵揔梡偡傞偲丄
(x+y)/(xy-1)=(3Z2-1)/(Z3-3Z)
俀亝Z 偱偁傞偺偱丂 (Z3-3Z)亗侽
堦曽丂xy=1丂側傞惍悢倶丄倷 偼 Z亜0傕峫椂偡傞偲
倶亖倷亖侾偺傒偱偁傞丅
偙偺偲偒丂arctan(1/Z)=兾/俇偱偁偭偰丄
Z=![]() /2丅
/2丅
懄偪丄Z偼惍悢偱偼側偄丅
傛偭偰丄(xy-1)亗侽 偲偟偰傛偄丅丂
埲忋傛傝椉曈偵丂(Z3-3Z)(xy-1)傪偐偗偰傕丄摍壙偱偁傞丅傛偭偰丄
(Z3-3Z)*(x+y)-(3Z2-1)*(xy-1)=0 ------(3-2)
偙偙偱栤戣侾摨條
x=Z+u y=Z+v 偲偍偗偽丂u,v偼惍悢偱側偗傟偽側傜側偄丅
傑偨丄Z亜x亜0傛傝 0亜u亜-Z -------(3-3)
(3-2)偵戙擖偟惍棟偡傞偲丄
(Z2+1)2+ 2Z*(u+v)*(Z2+1)+(3Z2亅1)uv =0 --(3-4)
Z2+1=Q亞5丂 偲偍偗偽
Q2+2Z*(u+v)*Q=亅(3Z2亅1)uv --(3-5)
亂栤戣俁偺曗戣亃
Z2+1=Q丂偲丂(3Z2亅1)丂偺岞栺悢偼崅乆俀偱偁傞丅
屳彍朄偵傛傟偽丂(3Z2亅1)-3Q=-4側偺偱丄岞栺悢偼崅乆係偱偁傞丅
Z偑嬼悢偺偲偒丂Q偼婏悢偱偁傝丄俀傪場悢偵傕偨側偄丅
Z偑婏悢偺偲偒丂Z=2n+1偲偡傞偲丂
Q=2+4(Z+2Z2)偱偁傝丄俀偺攞悢偱偁傞偑係偺攞悢偱側偄丅
傛偭偰丄=Q丂偲丂(3Z2亅1)丂偺岞栺悢偼Z偑婏悢偺偲偒俀丄嬼悢偺偲偒屳偄偵慺偱偁傞丅
(3-5)幃偺嵍曈偼Z偑婏悢偺偲偒Q偼嬼悢側偺偱丄俀Q偺攞悢偱偁傞丅
廬偭偰栤戣俁偺曗戣偵傛傝丂uv偼Q偺攞悢偱偁傞丅
Z偑嬼悢偺偲偒栤戣俁偺曗戣偵傛傝柍忦審偵丂uv偼Q偺攞悢偱偁傞丅
嵍曈亖Q2+2Z*(u+v)*Q=Q*(Q+2Z(u+v))
傛偭偰丄uv偼壓婰偱昞偝傟傞丅
uv =(A+1)Q A:惍悢 ----(3-6)
偙傟傪 (3-5)偵擖傟Q亜0偱彍偟偰惍棟偡傞偲丄
2Z(u+v)+ (3Z2亅1)A+4Z2=0 ---(3-7)
Z偲3Z2亅1 偼屳偄偵慺偱偁傞偐傜丂A偼Z偺攞悢偱側偗傟偽側傜側偄丅偡側傢偪
uv =( BZ+1)Q B:惍悢 ---(3-8)
師偵丂摿庩側応崌傪彍偒丂B=0偵尷傞偙偲傪徹柧偡傞丅
(3-5) 傪夝偔偲
亅v乛Q =(Q+2Zu)/(2ZQ+(3Z2亅1)u) ---(3-9)
0亜u亜-Z Z亞俀偱偁傞偺偱
暘巕亖|Q+2Zu|亙max((Z-1)2,|Z2-2Z-1|)= (Z-1)2
暘曣偼丂Z=俁n丂俁n+1 俁n-1 偵暘椶偟暘曣偺愨懳抣偺嵟彫傪専摙偡傞丅
暘曣偑嵟彫偵側傞偺偼
丂u=-(2Z3亄2Z)/(3Z2亅1) 晅嬤偱偁傞丅
Z=2 偵娭偟偰偼u=-1偱偁偭偰丄(3-9)傛傝丂v=-5/9 偱夝偼側偄丅
傛偭偰丂Z亞3
嘆丂Z=俁n偺偲偒 乮n亞1乯 u=-2n+兛偲偍偔偲
暘曣=8n+兛(27n2亅1)
丂丂=8/3Z + 兛(3Z2亅1)
8n=8,16,32 ,乧 偵懳偟
(27n2亅1)=26,107,242 乧..亜2*(8n)
傛偭偰暘曣偺愨懳抣偑嵟彫偵側傞偺偼丂兛亖侽偺偲偒偱
丂|暘曣|=8/3Z
師偵彫偝偄偺偼 兛亖亇侾偺偲偒偱偁偭偰丄
|暘曣|=min(乥27n2亅1+8n乥,乥 27n2亅1-8n乥 )
= 27n2亅1亅8n
乥暘曣乥/Z2= 俁 -8/3Z -1/ Z2..亞2
懄偪丂乥暘曣乥亞2 Z2
傑偲傔傞偲丂Z偑俁偺攞悢偺偲偒偱丂u=2Z/3偺応崌
丂乥亅v乛Q乥亙3/8(Z-1) 俀/Z
偦偺懠偺u偺偲偒
丂乥亅v乛Q乥亙0.5(侾亅1/Z) 2亙0.5
嘇丂Z=俁n-1偺偲偒 乮n亞2乯
u=-2n+1+兛偲偍偔偲
暘曣亖(9n2+4n-2) + 兛(27n2亅18n+2)
n亜2 偺偲偒
(9n2+2n-2)= 85,150 ,乧 偵懳偟
(27n2亅18n+2)=191,362, 乧..亜( 9n2+2n-2)
偱偁偭偰丄兛亖侽偱嵟彫偲側傞丅
n=2 偺偲偒偼兛亖亅侾偱嵟彫抣36
n=2 Z=5 偵偍偄偰丂36/Z2亜1
n亜俀 Z=3n-1丂偵偍偄偰丂
(9n2+2n-2)/ Z2亖侾亄乮3Z-n乯/ Z2亜1
懄偪丂乥暘曣乥亜 Z2
傑偲傔傞偲丂Z亞5丂偑俁偺攞悢亅侾偺偲偒
乥亅v乛Q乥亙(1-1/Z)2
嘊丂Z=俁n亄1偺偲偒 乮n亞1乯
仠丂u=-2n-1+兛偲偍偔偲
暘曣亖(9n2+4n-2) + 兛(27n2亄18n+2)丂
(-9n2+2n+2)= -5 , -30, -73 , -134 ,乧 偵懳偟
(27n2+18n+2)=47,146,299,506 乧..亜| -9n2+2n-2|*2
偱偁偭偰丄兛亖侽偱嵟彫偲側傞丅
偙偺偲偒暘曣偩偗偱偼丄
|-9n2+2n+2|/ Z2亖侾亄乮-3Z+n乯/ Z2亙1
偱偁傝丄偙偺傑傑偱偼丄梸偟偄寢壥偱偼側偄丅
廬偭偰暘巕傕峫椂偡傞偲丄(3-9)
for Z亞4
|亅v乛Q|
=(Q+2Zu)/(2ZQ+(3Z2亅1)u)
=(Z2亄2Z亅3)/(3Z2亅8Z亅侾)
埲忋偐傜丂for Z亜4丂丂|亅v乛Q|亙侾 偑惉棫偡傞丅
Z=4丂偵懳偟偰偼 (3-9) 偵傛傝
u=-1,-2,-3 v=-9/89 , - 1/42, -7/5丂偱夝偼柍偄丅
仠兛亖亇侾偺応崌偼嘆偲摨條偵偟偰
丂|暘曣乥亜2 Z2
傑偲傔傞偲丂Z(亞5)丂偑俁偺攞悢+侾偺偲偒
丂乥亅v乛Q乥亙 1
埲忋丂嘆嘇嘊傪傑偲傔傞偲
Z=3n u=-2n 偺応崌傪彍偄偰丂乥亅v乛Q乥亙1偱偁傞丅
|u|亝乮Z亅1乯偱偁傞偺偱
丂|uv/Q| =乥亅v乛Q乥|u|亙 乮Z亅1乯----(3-10)
堦曽丂(3-8)傛傝 B亗0丂偲偡傞偲
乥uv/Q乥 =乥 BZ+1乥亞|-Z+1|亖乮Z亅1乯偱偁傝 (3-10)偲柕弬偡傞丅
傛偭偰 B=0 丂懄偪丆
uv= Z2+1
埲忋傪傑偲傔傞偲丄乮俁亅侾乯傪枮懌偡傞丂倸丄倶丄y偑懚嵼偡傞偺偼壓婰俀働乕僗偵峣傜傟偨丅
(a)uv= Z2+1 丂丂倸亜係
(b)u = -2Z/3 丂丂丂Z=3n
仠(a)偺応崌
(3-4)偵戙擖偟惍棟偡傞偲
2Z+(u+v) = 0丂---(3-11)
(a)偲(3-11)傪枮懌偡傞u,v偼丂壓婰俀師曽掱幃偺夝偱偁傞
t*t+2Z*t+ Z2+1=0
敾暿幃
丂D= Z2亅乮Z2+1乯亖亅侾亙侽
u,v偼幚悢偱偼側偄丅
傛偭偰丂(a)偺応崌偵夝偼懚嵼偟側偄丅
仠(b)偺応崌
(3-9)偵Z=3n u=-2n傪戙擖偟惍棟偡傞偲
-v丂亖( 9 n2+1)*(3n2亅1 )乛8n
亊俉&惍棟丂偡傞偲
-8v亖 27 n3亅6 n2亅乮1乛n乯
1/n偑惍悢側偺偼丂n=1偺傒偱偁傞丅
偙偺偲偒丂v=-5/4 偱 v 偼惍悢偱偼側偄丅丂丂
埲忋偱丂夝偑懚嵼偟側偄偙偲偑徹柧偝傟偨丅
亂栤戣俁姶憐亃
僑乕儖僨儞僂傿乕僋偵侾偮偐俀偮"丠"傪偮傇偦偆偲巚偄棫偭偨偑100擭栚丄崑偄傕偺偵僴儅僢僥偟傑偭偨丅
偡偖偵弌棃偦偆偵尒偊偨偺偱偡偑丄偐偔偺偛偲偔戝榑暥偵側偭偰偟傑偄傑偟偨丅
撉傒曉偟偰傒偰傕丄摢偺崿棎傪斀塮偟偰偍傝丄撉傒偵偔偄傕偺偲巚偄傑偡丅
傕偆彮偟僗僢僉儕偱偒傞偲偙傠傕偁傝傑偡偑丆偄偢傟偵偟偰傕丄僄儗僈儞僩側夝朄偑梡堄偝傟偰偄傞偲悇嶡偟傑偡偺偱丄傗偭偨偲尵偆徹嫆偲偟偰丄偙偺傑傑幐楃側偑傜採弌偄偨偟傑偡丅
乮杮壒偼彂偒捈偡偺偑柺搢側偺偱偡偑丅乯
亂栤戣係亃
Arctan(1/x)+Arctan(1/y)=係Arctan(1/z)丂丂丂-----(4-1)

亂栤戣係夝朄亃
Z=1偺偲偒塃曈偼 兾偱偁傞偑
嵍曈偺嵟戝偼 x=y=1偺偲偒俀兾/係偱偁偭偰丄惉棫偟側偄丅
傛偭偰丄俀亝Z丂偲偟偰傛偄丅
傑偨丄(3-1)偐傜 彮側偔偲傕x,y偺壗傟偐偼惓偐偮倅枹枮偱柍偗傟偽側傜偢丆
Z亜x亜0丂偲偡傞丅
偙偺偲偒 |y|亞x偱偁傞偲偟偰傛偄丅
乮4乯偲乮6乯傪乮4-1乯偵揔梡偡傞偲丄
(x+y)/(xy-1)=(4Z3-4Z)/(Z4-6Z2+1)
(ZSUP>4-6Z2+1)亗侽丂偱偁傞丅
堦曽丂xy=1丂側傞惍悢倶丄倷 偼 Z亜0傕峫椂偡傞偲
丂倶亖倷亖侾偺傒偱偁傞丅
偙偺偲偒丂arctan(1/Z)=兾/俉偱偁偭偰丄
Z=(1+![]() )丅丂
)丅丂
懄偪丄Z偼惍悢偱偼側偄丅
傛偭偰丄(xy-1)亗侽 偲偟偰傛偄丅
埲忋傛傝椉曈偵
丂(Z4-6Z2+1) (xy-1)傪偐偗偰傕丄摍壙偱偁傞丅
懄偪丄
(Z4-6Z2+1)*(x+y)- (4ZSUP>3-4Z)*(xy-1)=0
丂丂丂------(4-2)
偙偙偱栤戣侾摨條
x=Z+u y=Z+v 偲偍偗偽丂u,v偼惍悢偱側偗傟偽側傜側偄丅
傑偨丄Z亜x亜0傛傝丂0亜u亜-Z丂丂丂-------(4-3)
(4-2)偵戙擖偟惍棟偡傞偲丄
2Z(Z2+1)2 +(u+v)(3Z2-1)(Z2+1)+4Z*(Z2-1)uv=0
丂丂丂------(4-4)
Z2+1=Q亞5丂 偲偍偗偽
2ZQ2+(3Z2-1)*(u+v)*Q
=亅4Z(Z2亅1)uv丂丂丂------(4-5)
Q 偲丂亅4Z(Z2亅1) 偼崅乆丂俀傪岞栺悢偲偟偰傕偮偩偗偱偁傞丅
傛偭偰
uv =Q/2*(1+A) A:惍悢丂丂丂----(4-6)
(4-5)偵戙擖偡傟偽
(3Z2-1)*(u+v)=亅俀Z(Z2亅1)A亅4ZSUP>3
(3Z2-1) 偲Z偼屳偄偵慺偱偁傝丄偐偮塃曈偼係偺攞悢丄
(3Z2-1)偼係偺攞悢偱側偄偺偱
u+v=俀Z乮B亅侾乯丂丂丂B:惍悢丂丂丂---(4-7)
(4-5)偵戙擖偡傟偽
(3Z2-1)*(B-1)
=亅(Z2亅1)A亅俀Z2
A = 亅乮(3Z2-1)*B亄1-Z2乯乛乮Z2亅1乯
丂= 1 亅(3Z2-1)*B乛乮Z2亅1乯
(3Z2-1) 偲丂乮Z2亅1乯 偼丂崅乆俀傪岞栺悢偲偟偰傕偮丅廬偭偰
B偼乮Z2亅1乯/2 偺攞悢丂偡側傢偪
A=1 亄(3Z2-1)/2*C C:惍悢
寢嬊
uv = Q + Q *(3Z2-1)/4*C ---(4-8)
堦曽丂乮4亅4乯傪-v偵偮偄偰夝偔偲
-v= Q* (2Z(Z2+1)+(3Z2-1)u)/( (3Z2-1)(Z2+1)+4Z*(Z2-1)u) ---(4-9)
偙偙偱丂栤戣俁偲傎傏摨偠宍幃偑峔惉偝傟偨丅
愭偵C=0偺応崌傪媗傔偰偍偔偲丆
uv=Z2+1
u+v=亅俀Z
偙偺曽掱幃傪枮懌偡傞丂u,v偼丂t*t+2Zt+ Z2+1=0 偺崻
敾暿幃丂D=-1 亙0
傛偭偰丂u,v偼嫊崻偱偁傝丄惍悢偱偼側偄丅
(4-9)偺暘曣偐傜丂Z亜桳尷抣偵偍偄偰丂
Z=4n丂u=-3n 偺偲偒偩偗丂|-v/Q/Z|偼戝偒偔側傝
偦傟埲奜偱偼侾埲壓偱丂C亖0偱側偗傟偽側傜側偔側傞偲徹柧偱偒傞偲栤戣俁偐傜悇應偝傟傞丅
偙偙偱偼丄彮偟僒儃偭偰丆偦偺徹柧偼偣偢丄梊應偑惓偟偄偐丂寁嶼婡偱偟傜傋偨丅
壓昞偼丂Z亝侾侽侽傑偱傪PC偱挷傋偨寢壥偺偆偪丄
|-v/Q/Z|亜0.375埲忋偺傕偺傪堦棗偵偟偨昞偱偁傞丅
梊應偳偍傝丂Z亝侾侽侽丂偵偍偗傞桞堦偺夝
Z=5 u=-4 v=234 偑娷傑傟偰偄傞丅
傑偨丂Z亞侾俀丂偵偍偄偰偼丂Z偑係偺攞悢偱丂
u=-3Z/4偺応崌偺傒偑儕僗僩傾僢僾偝傟偰偄傞丅
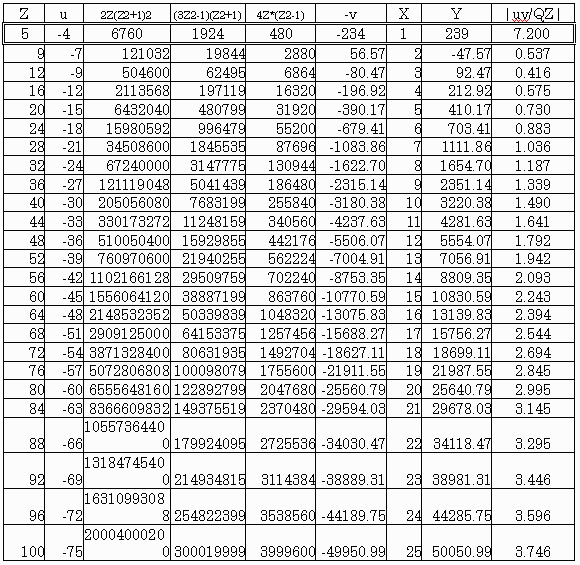
嵟屻偵丂Z=4n u=-3n 倸亜侾俀丂偺応崌偵偼夝偑柍偄偙偲傪徹柧偡傞丅
(4-9)偵偙傟傜傪戙擖偟惍棟偡傞偲丄
-v= (16n2+1)n(11亅16n2)/(80n2亅1)
(a) 丂n偲丂(80n2亅1)偼屳偄偵慺
(b) (16n2+1) 偲丂(80n2亅1)偼s屳彍朄偱
(16n2+1) 偲丂-6亖亅俀亊俁
16n2+1 偼婏悢側偺偱丂2偺栺悢偼柍偄
俁偺攞悢偐偳偆偐偼丂丂n2+1丂mod 3 偱峫偊傟偽傛偔
n=0,1,2 偵懳偟偰 1,2,2偱偁偭偰丄俁偺攞悢偱偼側偄丅
傛偭偰(16n2+1) 偲丂(80n2亅1)偼屳偄偵慺
(c) (-16n2+11) 偲丂(80n2亅1)偼s屳彍朄偱
(-16n2+11) 偲丂-54亖亅俀亊俁3
-16n2+11 偼婏悢側偺偱丂2偺栺悢偼柍偄
俁偺攞悢偐偳偆偐偼丂-n2+2丂mod 3 偱峫偊傟偽傛偔
n=0,1,2 偵懳偟偰 2,1,1偱偁偭偰丄俁偺攞悢偱偼側偄丅
傛偭偰(-16n2+11) 偲丂(80n2亅1)偼屳偄偵慺
傑偨丂暘曣偼侾偱偼側偄丅
廬偭偰丆暘巕偼暘曣偺攞悢偱柍偔丄倴偼惍悢偱偼側偄丅
埲忋偐傜丂(4-1)偺夝偼
Z亖俆丂X=1丂Y=239 偺傒偱偁傞乮傜偟偄乯丅
亂栤戣係姶憐亃
偪傖傫偲偟偨徹柧偼丄旀傟偨偺偱僷僗丅
婡夛偑偁傟偽暿儖乕僩傪栚巜偡偮傕傝丅
仧弌戣幰偺僐儊儞僩
偐側傝抶偔側偭偰偟傑偄傑偟偨偑丆奆偝傫夝摎偁傝偑偲偆偛偞偄傑偟偨丅
傑偢栤戣1偵偮偄偰偼丆奆偝傫堎榑偼側偄偲巚偄傑偡丅
師偵栤戣2偵偮偄偰偱偡偑丆帺桼側敪憐傪偟偰傕傜偆偨傔偵丆偐側傝敊慠偲偟偨栤戣愝掕傪偟偰偟傑偄傑偟偨丅
Y.M.Ojisan偝傫偺夝摎偼傕偪傠傫惓夝偱偡偑丆偛帺恎傕偍偭偟傖偭偰偄傞傛偆偵丆乽偡傋偰偺乿夝傪嬶懱揑偵媮傔傞偙偲偑偱偒側偄偲偄偆擄揰偑偁傞偱偟傚偆丅
偦偙偱丆栤戣2傪埲壓偺傛偆偵夵傔偨偄偲巚偄傑偡丅
偦偺偨傔偵丆傑偢師偺傛偆偵掕媊偟傑偡丅
掕媊.
惓偺惍悢a偵懳偟偰丆惍悢楍(un(a)), (vn(a)) (n伕Z)傪師偺傛偆偵掕媊偡傞丅
un(a)亄vn(a)併d亖(a亄併d)n (n伕Z)
偨偩偟丆d亖a2亄1偲偡傞丅
偙偺偲偒丆師偺栤戣偵挧愴偟偰傒偰偔偩偝偄丅
栤. 惓偺惍悢x, y, z (x亙y)偑曽掱幃
| Arctan( | 1 x | )+Arctan( |
1 y | )亖2Arctan( |
1 z | ) |
傪枮偨偡偨傔偺昁梫廫暘忦審偼丆偁傞惓偺惍悢a偍傛傃n偑懚嵼偟偰
x亖u2n-1(a), y亖u2n+1(a), z亖v2n(a)
偲昞偝傟傞偙偲偱偁傝丆傑偨曽掱幃
| Arctan( | 1 x | )亅Arctan( |
1 y | )亖2Arctan( |
1 z | ) |
傪枮偨偡偨傔偺昁梫廫暘忦審偼丆偁傞惓偺惍悢n偑懚嵼偟偰
x亖u2n-1(1), y亖u2n+1(1), z亖u2n(1)
偲昞偝傟傞偙偲偱偁傞偙偲傪帵偣丅
偝偰丆巆傞偼栤戣3偍傛傃4偱偡偑丆巹偑梡堄偟偰偄偨夝朄傕婎杮揑偵Y.M.Ojisan偝傫偲摨條偺応崌暘偗偵婎偯偄偰偄傑偡丅
栤戣3,4偄偢傟傕摨條偺曽恓偱偡偺偱丆埲壓偱偼栤戣3偵偮偄偰偩偗尵媦偟偨偄偲巚偄傑偡丅
傑偢丆偙偺榖戣偵娭偟偰抦傜傟偰偄傞掕棟傪堦偮弎傋偰偍偒傑偡丅
掕棟1.1乮St鴕mer乯.
惍悢k, m, n, x, y偵懳偟偰丆晄掕曽掱幃
| k Arctan 1亖m arctan( | 1 x | )亄n arctan( |
1 y | ) |
偼杮幙揑偵師偺4偮偺夝偺傒傪帩偮丅
| Arctan 1亖Arctan( | 1 2 | )+Arctan( |
1 3 | ), |
| Arctan 1亖2Arctan( | 1 2 | )-Arctan( |
1 7 | ), |
| Arctan 1亖2Arctan( | 1 3 | )+Arctan( |
1 7 | ), |
| Arctan 1亖4Arctan( | 1 5 | )-Arctan( |
1 239 | ), |
偦傟偐傜丆曗戣傪堦偮梡堄偟偰偍偒傑偡丅
曗戣1.2.
惓偺惍悢k偵懳偟偰丆0偱側偄惍悢x, y, z偑曽掱幃
| (1.1) Arctan( | 1 x | )+Arctan( |
1 y | )亖k Arctan( |
1 z | ) |
傪枮偨偡側傜偽丆偁傞屳偄偵慺側惍悢a, b偑懚嵼偟偰丆師偑惉傝棫偮丅
(1.2) a(x亄i)(y亄i)亖b(z亄i)k. 乮i偼嫊悢扨埵乯
| 偝傜偵丆偁傞惍悢0亝e亝 | k 2 | 偵懳偟偰丆a=2e偲昞偝傟傞丅 |
棯徹.
兛亖(x亄i)(y亄i)(z亄i)-k伕Q(i)偲偍偔偲丆
(1.1)傛傝arg兛伕兾Z偱偁傞偐傜丆兛偼桳棟悢偱偁傞丅
傛偭偰丆(1.2)偑惉傝棫偮丅
崱丆婏慺悢p偑a傪妱傝愗傞偲偡傞偲丆Z[i]偺堦堄暘夝惈傛傝丆
p偼z亄i傪妱傝愗傞偙偲偵側傝柕弬丅
偟偨偑偭偰丆a=2e (e亞0)偲昞偝傟傞偑丆
e亜k/2偲偡傞偲丆嵞傃Z[i]偺堦堄暘夝惈傛傝丆2偑z亄i傪妱傝愗傞偙偲偵側傝柕弬丅
| 傛偭偰丆e亝 | k 2 | 偲側傞丅 |
傑偨丆Taylor偺掕棟傛傝師偑惉傝棫偮偙偲偵拲堄偟偰偔偩偝偄丅
曗戣1.3.
擟堄偺幚悢0亙t亙1偍傛傃惍悢n亞0偵懳偟偰師偺晄摍幃偑惉傝棫偮丅
| Arctan t 亙t亅 | t3 3 | + | t5 5 | -...亄 | t4n+1 4n+1 | , |
| Arctan t 亜t亅 | t3 3 | + | t5 5 | -...亅 | t4n+3 4n+3 |
偙傟偱弨旛偑偱偒傑偟偨丅
亂栤戣俁偺夝摎亃
傑偢掕棟1.1傛傝丆x亞2, z亞x亄1亞3偲偟偰傛偄丅
傑偨曗戣1.2傛傝丆偁傞惍悢a, b偑懚嵼偟偰
a(x亄i)(y亄i)亖b(z亄i)3, 1亝a亝2.
椉曈偺幚晹偍傛傃嫊晹傪斾妑偡傟偽丆
(1.3a) a(xy亅1)亖b(z3亅3z),
(1.3b) a(x亄y)亖b(3z2亅1).
摿偵(1.3b)傛傝丆
| |y|亖| | b(3z2亅1) a | 亅x| |
| 丂亞 | |b|(3z2亅1) a | 亅x |
| 丂亜 | 3z2亅1 2 | 亅z |
| 丂亜z2. |
崱丆z亝3x亅1偲壖掕偡傞偲丆
| 丂Arctan( | 1 x | )+Arctan( |
1 y | )-3Arctan( |
1 z | ) |
| 亙Arctan( | 3 z亄1 | )+Arctan( |
1 z2 | )-3Arctan( |
1 z | ) |
| 亙 | 3 z亄1 | + |
1 z2 | -3( |
1 z | - |
1 3z3 | ) |
| 亖 | -(2z2亅2z亅1) z3(z亄1) |
| 亙0丂偲側傝柕弬丅 |
堦曽丆z亞3x亄1偲壖掕偡傞偲丆
|y|亜z2亜3x(3x亄1)偱偁傞偐傜丆
| 丂Arctan( | 1 x | )+Arctan( |
1 y | )-3Arctan( |
1 z | ) |
| 亜Arctan( | 1 x | )亅Arctan( |
1 3x(3x亄1) | )-3Arctan( |
1 3x亄1 | ) |
| 亜 | 1 x | 亅 |
1 3x3 | - |
1 3x(3x亄1) | 亅3( |
1 3x亄1 | ) |
| 亖 | 2x2亅3x亅1 3x3(3x亄1) |
| 亜0丂偲側傝柕弬丅 |
嵟屻偵丆z亖3x偲壖掕偡傞偲丆(1.3)傛傝丆
1佭(xy亅1)(3z2亅1)亖(x亄y)(z3亅3z)佭0 (mod x)
偲側傝柕弬丅
埲忋偱丆戣堄傪枮偨偡x, y, z偑懚嵼偟側偄偙偲偑帵偝傟偨丅
嵟屻偵僐儊儞僩偱偡偑丆乽僄儗僈儞僩乿偐偳偆偐偼暿偲偟偰丆懡彮抁偔偼側偭偨偱偟傚偆偐丅
偟偐偟丆撪梕傪傛偔尒偰傕傜偆偲暘偐傞傛偆偵丆偄偢傟傕杮幙揑偵R偺戝彫娭學乮埵憡揑惈幙乯傪梡偄偰偄傑偡丅
偦傕偦傕巹偑偙偺栤戣傪搳峞偟偨棟桼偺堦偮偼丆偙傟傪弮悎偵戙悢揑偵帵偡偙偲偑偱偒側偄偐偲偄偆揰偱偟偨丅
巆擮側偑傜丆偄傑偩弮戙悢揑側徹柧偼尒偮偐偭偰偄側偄偺偱丆堷偒懕偒忣曬傪偍懸偪偟偰偄傑偡丅