◆宮城県 アンパンマン さんからの解答。
【問題1】
全てのmn個のベクトルφiは独立であるため『ホワイトノイズ 』問題の解答をそのまま利用すると
E[|W|2]
| = | 1 4 | | | m | n Σ i=1 | φi | |2+ | 1 4 | ( | n Σ i=1 | m|φi|2) |
| = | m2 4 | | | n Σ i=1 | φi | |2+ | m 4 | ( | n Σ i=1 | | | φi | | | 2) |
| = | m 4 |
別の解法だと
Yi=φiの個数(0,1,...,m)、
| k個あるときの確率= | mCk 2m |
E[|W|2]
=E[X]
=E[E[X|Yn]]
| = | m Σ k=0 |
mCk 2m |
E[|Zn-1+kφn|2] |
| = | m Σ k=0 | k2 | mCk 2m |
|φn|2+ | m Σ k=0 | 2k | mCk 2m |
φn・E[Zn-1]+ | ( | m Σ k=0 |
mCk 2m |
) | E[|Zn-1|2] |
| = | m-1 Σ k=0 | m(k+1) | m-1Ck 2m |
|φn|2+ | m-1 Σ k=0 | 2m | m-1Ck 2m |
φn・E[Zn-1]+E[|Zn-1|2] |
| = | m2+2m 4 |
|φn|2+m φn・E[Zn-1]+E[|Zn-1|2] |
E[Zn-1]
=E[Y1]+E[Y2]+...+E[Yn-1]
| = | n-1 Σ i=1 |
m Σ k=0 |
k mCk 2m | φi |
| = | n-1 Σ i=1 | m | m-1 Σ k=0 |
m-1Ck-1 2m | φi |
| = | m 2 | Φn-1より |
E[|W|2]
| = | m(m+1) 4 | |φn|2+ | m2 2 | φn・ Φn-1+E[|Zn-1|2] |
| = | m(m+1) 4 | ( | n Σ i=1 | |φi|2)+ | m2 2 | n Σ i=2 | φi・ Φi-1 |
| n Σ i=2 | φi・ Φi-1 |
| = | 1 2 | ( | | | n Σ i=1 | φi | |2- | n Σ i=1 | |φi|2) |
より
E[|W|2]
| = | m2 4 | | | n Σ i=1 | φi | |2+ | m 4 | ( | n Σ i=1 | | | φi | |2) |
| = | m 4 |
【問題2】
Yi=φiの個数(0,1,...,m)、
| k個あるときの確率= | 1 m+1 |
X=|Y1+Y2+...+Yn|2 ,
Zj=Y1+Y2+...+Yj
Φj=φ1+φ2+...+φj とすると
E[|W|2]
=E[X]
=E[E[X|Yn]]
| = | m Σ k=0 |
1 m+1 | E[|Zn-1+kφn|2] |
| = | 1 m+1 | m Σ k=0 |
k2 |φn|2+ | 1 m+1 | m Σ k=0 |
2k φn・E[Zn-1]+ | 1 m+1 | ( | m Σ k=0 | 1) | E[|Zn-1|2] |
| = | m(2m+1) 6 | |φn|2 + m φn・E[Zn-1]+E[|Zn-1|2] |
E[Zn-1]
=E[Y1]+E[Y2]+...+E[Yn-1]
| = | n-1 Σ i=1 |
m Σ k=0 | k m+1 | φi |
| = | m 2 | Φn-1より |
E[|W|2]
| = | m(2m+1) 6 | |φn|2+ | m2 2 | φn・ Φn-1+E[|Zn-1|2] |
| = | m(2m+1) 6 | ( | n Σ i=1 | |φi|2)+ | m2 2 |
n Σ i=2 |
φi・Φi-1 |
| n Σ i=2 |
φi・Φi-1 |
| = | 1 2 | ( | | n Σ i=1 |
φi | |2- | n Σ i=1 |
|φi|2) |
より
E[|W|2]
| = | m2 4 | | | n Σ i=1 | φi | | | 2+ | m(m+2) 12 | ( | n Σ i=1 | |φi|2) |
| = | m(m+2) 12 |
◆山梨県 Footmark さんからの解答。
2次元から3次元、等長から任意の長さと、『ホワイトノイズ 』がより一般化されました。
ですから、『ホワイトノイズ 』は『ホワイトノイズ Part2』の内の1ケースです。
それ故、『ホワイトノイズ 』同様に平面上の等長ベクトルとしても
| n-1 Σ i=0 | |φi|2=1 となる筈です。 |
【問題1】
前問『ホワイトノイズ 』の期待値を利用した省エネ解答です。
『ホワイトノイズ 』同様に平面上の等長ベクトルとして考えます。
すると、これはmn個のベクトルを、重複を許さず他と独立に1/2の確率で選ぶ場合と同じです。
| mn-1 Σ i=0 | φi=0 |
| |φi|= | 1 | とすれば、『ホワイトノイズ 』同様に |
| E(|W|2)は | 1 4 | の筈です。 |
| ところが、|φi|= | 1 | ですから、 |
| E(|W|2)= | 1 4 | ( | 1 | / | 1 | )2 | = | m 4 |
【問題2】
『ホワイトノイズ 』同様に平面上の等長ベクトルとして考えます。
期待値はnによらないので、n=2としてみると、
| |+φ|=|−φ|= | 1 |
また、+φと −φ の個数の組合せの数は (m+1)2
各組合せにおけるベクトルの長さの2乗は以下のとおりです。
横軸(→),縦軸(↓)は +φ,−φ のそれぞれの個数(0〜n)です。
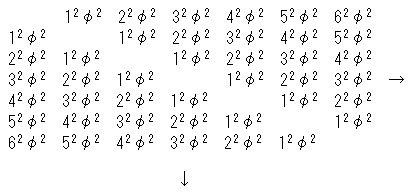
| φ2= | 1 2 | なので、これらの合計は |
| m Σ i=1 | i Σ j=1 | j2= | 1 12 | *m*(m+1)2*(m+2) |
よって求める期待値E(|W|2)は
E(|W|2)
| = |
(m+1)2 |
| = | 1 12 | *m(m+2) |
◆出題者のコメント。
【コメント#1】
アンパンマンさん、Footmark さん、正解です。
ただし、Footmark さんの問題2解答は証明というより予測でしょう。
アンパンマンさんの解答によれば、「空間」は3次元座標空間に限らず任意次元のベクトル空間で成立することが分かります。
蛇足ですが、φを使う使わないはもう少し一般化できて、下記のようになります。
尚、下記では縮約記法を用います。
δijはi=j のときのみ1、 υiは常に1です。
βiは平均がμで標準偏差がσなる確率分布に従い、
各βiは独立事象とし、以下でWを定義します。
φ性質:
υiφi=0
φiφi=1
β性質:
E(βi)=μ
E(βiβj)=μ2υiυj +σ2δij
W定義:
W=βiφi
このとき、
E(|W|2)
=E(βiφiβjφj)
= E(βiβj)φiφj
=μ2(υiφi) (υjφj) +σ2φiφi
=0*μ2+ 1*σ2
=σ2
すなわち、βiの標準偏差が分かればよいのです。
◆山梨県 Footmark さんからのコメント。
お恥ずかしいながら、【問題2】の証明はご指摘のとおり証明にはなっていませんでした。~~;
まだ証明されてもいない「期待値はnによらない」を前提にするのは論理の飛躍でした。
【問題1】や『ホワイトノイズ』 のケースでは、結果より「期待値はnによらない」は証明されたので勘違いしてしまいました。
◆東京都 はにゃん さんからの解答。
【問題1】
ψ[i]=Σφ[i] (i=固定の重複和)とおく.
ψ[i],|ψ[i]|2,ψ[i]・ψ[j]の期待値は,それぞれ
E[ψ[i]]
| = | m Σ k=0 | mCk 2m |
*k*φ[i] |
| = | 1 2m |
*φ[i]* | m Σ k=0 | k*mCk |
| = | 1 2m |
*φ[i]*m*2m-1 |
| (↑ | m Σ k=0 | k*mCk=m*2m-1) |
| = | m 2 |
*φ[i] |
E[|ψ[i]|2]
| = | m Σ k=0 | mCk 2m |
*k2*|φ[i]|2 |
| = | 1 2m |
*|φ[i]|2* | m Σ k=0 | k2*mCk |
| = | 1 2m |
*|φ[i]|2*m(m+1)*2m-2 |
| (↑ | m Σ k=0 | k2*mCk=m(m+1)*2m-2) |
| = | m(m+1) 4 |
*|φ[i]|2 |
E[ψ[i]・ψ[j]]
| =E[ψ[i]]・E[ψ[j]] (←ψ(i)とψ(j)は独立) |
| = | m2 4 |
*φ[i]・φ[j] (i≠j) となる.これより, |
E[|W|2]
| =E | [| | Σ i | ψ[i] | |2 | ] |
| =E | [ | Σ i | | | ψ[i] | |2 | ]+E[ | Σ i≠j | ψ[i]・ψ[j] ] |
| = | Σ i | E[|ψ[i]|2]+ | Σ i≠j | E[ψ[i]・ψ[j] ] |
| = | m(m+1) 4 | * | Σ i | |φ[i]|2+ | m2 4 | * | Σ i≠j | φ[i]・φ[j] |
| = | m 4 | * | Σ i | |φ[i]|2+ | m2 4 | * | | | Σ i | φ[i] | |2 |
| = | m 4 | *1+ | m2 4 | *0 |
| = | m 4 |
【問題2】
ψ[i]=Σφ[i](i=固定の重複和)とおく.
ψ[i],|ψ[i]|2,ψ[i]・ψ[j]の期待値は,それぞれ
E[ψ[i]]
| = | m Σ k=0 | 1 m+1 | *k*φ[i] |
| = | 1 m+1 | *φ[i]* | m Σ k=0 | k |
| = | 1 m+1 | *φ[i]* | m(m+1) 2 | (← | m Σ k=0 | k | = | m(m+1) 2 | ) |
| = | m 2 | *φ[i] |
E[|ψ[i]|2]
| = | m Σ k=0 | 1 m+1 | *k2*|φ[i]|2 |
| = | 1 m+1 | *|φ[i]|2* | m Σ k=0 | k2 |
| = | 1 m+1 |
*|φ[i]|2* | m(m+1)(2m+1) 6 |
(← | m Σ k=0 | k2= | m(m+1)(2m+1) 6 | ) |
| = | m(2m+1) 6 |
*|φ[i]|2 |
E[ψ[i]・ψ[j]]
| =E[ψ[i]]・E[ψ[j]] (←ψ(i)とψ(j)は独立) |
| = | m2 4 |
*φ[i]・φ[j] (i≠j)となる.これより |
E[|W|2]
| =E | [| | Σ i | ψ[i] | |2 | ] |
| =E | [ | Σ i | |ψ[i]|2] | +E | [ | Σ i≠j | ψ[i]・ψ[j]] | ] |
| = | Σ i | E[|ψ[i]|2]+ | Σ i≠j | E[ψ[i]・ψ[j] ] |
| = | m(2m+1) 6 | * | Σ i | |φ[i]|2+ | m2 4 | * | Σ i≠j | φ[i]・φ[j] |
| = | m(m+2) 12 | * | Σ i | |φ[i]|2+ | m2 4 | * | | | Σ i | φ[i]|2 |
| = | m(m+2) 12 | *1+ | m2 4 | *0 |
| = | m(m+2) 12 |
(こめんと)
| Part2のように大きさの和 | Σ i | |φ[i]|だけで十分だと思います. |
◆出題者のコメント。
【コメント#2】
はにゃん さん、解答&(こめんと)ありがとうございます。
御指摘のとおりです。
『ホワイトノイズ』(part1)は『ホワイトノイズ@SETI@HOME』への布石です。
ただ、これでは純粋数学FAN(Myself?)からは御指摘のような不満が出るかと思い、『ホワイトノイズ Part2』(含 コメント#1)を追加しました。
信号解析の常套手段はスペクトル分析です。
大量のデジタルデータを高速で処理するには、その中でもFFT(高速フーリエ変換)が一般的です。
この場合、サンプリング時間は一定で、サンプリング数は2Nに決まっています。
(最近3Nもありますが)
そしてサンプリング時間一定が、過剰と御指摘の、φiの等長条件に繋がります。
また、φjはフーリエ変換での exp(iωΔtj) 相当であって元は複素数なので、布石としては2次元で十分なのです。
また逆に2次元ベクトル空間でベクトルのまま証明できれば、多次元(含1次元)への拡張はNo-Excuse でOKですから、難しくすることも無いと考えました。
フーリエ変換と言えば大学レベルですが,『ホワイトノイズ』のように置き換えれば、ベクトルと確率ですから、証明が容易です。
そうすると、『ホワイトノイズ@SETI@HOME』がパズル問題に落ちるので、解答が出易くなるであろうという目論見です。