◆愛知県 Y.M.Ojisan さんからの解答。
【問題1解答】 N+1個
【証明】
1次元では2個、2次元で3個、3次元で4個であるからN次元でN+1個と予測される。
また点間距離を1とするとき、重心と点の距離は
1次元では√(1/2*2)、2次元では√(2/2*3)、3次元では√(3/2*4)であるので、
N次元では√(N/2*(N+1))と予測される。
いまN次元において、点間距離がすべて1である点の最大数がN+1で、
重心との距離が√(N/2*(N+1))であるとする。 --(1)
N+1次元において、点間距離がすべて1である点がm個あるとし、そのうちからN+1個の点を取り出すとする。
これらのN+1個の点はそれらの重心Oを原点とする座標系において、ある方向Dに直行するN次元の空間の点として表すことが可能である。
又逆に(1)により残りのm-N-1,個の点はD方向の成分を必ず持たなければならない。
なお、これらN+1個の点の原点Oから距離は(1)より√(N/2*(N+1))である。
残りのm-N-1個の点はN+1個の点から全て1の距離になければならないので、Dに直交する成分が全て等しくなければならず、それは直交する場合だけである。
(線形代数による。詳細略)
よって、残りのm-N-1個の点はD方向上の点でなければならず、あっても最大両側2個である。
ところが重心Oとの距離は
√(1-N/2(N+1))=√((N+2)/2(N+1))>1/2であるのでこの2点間の距離は1を超過し、一方のみ採用可能です。
よってm=N+2です。
またこれらm個の重心O’からの距離は
(N+1)/(N+2)√((N+2)/2(N+1))=√((N+1)/2(N+2))
で(1)においてN=N+1とした場合になっています。
以上
【問題2解答】
すくなくとも N=2k-1, のとき存在する。
K:非負整数
Nが偶数で、N+1が平方数でない場合は存在しない。
【まえおき】
RN空間は座標値の正負により2N個の象限に分けられ、
N+1がその約数(2k)なら各点を均一に振り分けることが可能であり、可能性が高いと言えます。
【条件変換】
本問題の条件を整理すると、次の連立2次ディオファントス問題になります。
ANT*AN=C*(N*IN-DN) ----(2)
ここで AN:N×N整数値行列、C:整数
D N :N×N行列で対角成分が0、非対角成分が1のもの。
∵N次元において解が存在したとするとき、その座標値をN+1倍したものを考えるとその重心も格子点上である。
従って、重心が原点であるとして一般性を失わない。
そのような座標において、N+1個の頂点の座標を列ベクトルとして並べたN×N+1の行列をBNとする。
このとき、条件より
BNT*BN=α*IN+1+β*DN+1 -----(3)
と表すことができます。
ここでαは原点から頂点までの距離の2乗、βは2頂点間の内積値で整数です。
ところで要素が全部1の列ベクトルをSNとするとき、
原点を重心に採っているので、BNT *SN+1=0です。
従って、BN =(AN,- AN* SN)です。
(3)に代入すると、
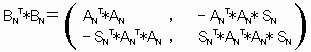
以上と(3)より
ANT*AN=α*IN+β*DN であり、
-ANT*AN* SN=β*SNでなければなりません。
すなわち {-α*IN-β*DN}*SN=βSN です。
計算すると、-α-(N-1)β=βより
α=CN、β=-C、Cは整数です。
即ち(2)式です。
【実例 N=1のとき】
A1=1とすれば ANT*AN=1 で(2)の形になっています。
【実例 N=3のとき】
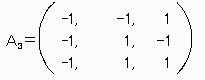
とおけば、ANT*ANの対角成分は3、非対角成分は-1,になっており、(2)の式になっています。
【N=2k-1,C=1のとき】
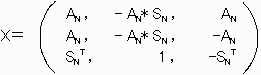
とおけば、
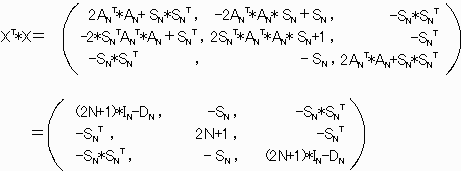
すなわち XT*X=(2N+1)*IN-DN であって
X=A2N+1の性質をもち、2N+1=2k+1-1,C=1です。
たとえばN=7のとき下記のようにA3を用いて作成できます。
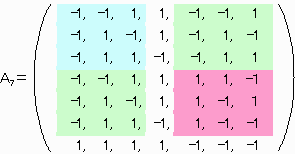
【その他の場合で分かるもの】
(2)式の行列式をとると下記である。
|A|2=CN(N+1)N-1
従ってN=2Mであるときは
|A|2=(CM(N+1)M-1)2*(N+1)より
N+1が平方数でなければならない。
従って N=2、4、6、 10、12、14、16、18 。。。は存在しない。
逆にN=8(C=2)は下記のような解等多数が存在している。
なお、次のN=24についてはPC探索の限界を超えており未確認である。
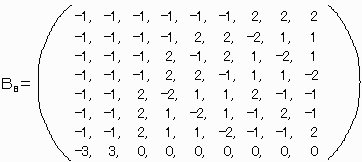
一方、N=2M+1であるときは
|A|2=(CM(N+1)M)2*Cより、Cは平方数でなければならない。
N=5の場合をPCでC=12〜232まで探索したが解はなかった。
N=7は前述のとおり存在し、N=9,N=11についてもPCで探索して下記の解等を得た。
N=13はなさそうであるが、PCの限界を超えて未確認である。
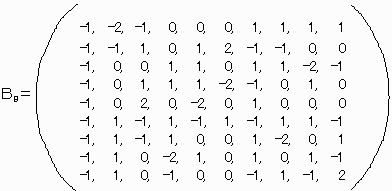
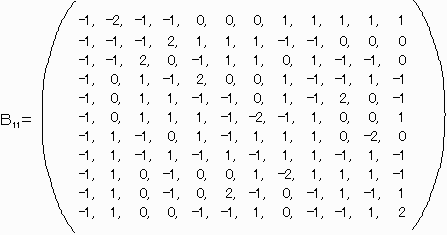
確認できたもの
可能:1、3、7、8、9、11、15、2K−1
不可能:2、4、6、10、12、14、16、N+1が平方数でない偶数
?:5、13
【PS】
ここのところこの問題をずっと考えていたのですが、難しい問題です。
長期間解答者がないようですので、途中ですが報告いたします。
N=5がないこと(?)を証明したいですね。
◆出題者のコメント。
解答ありがとうございます。
実はこの問題、私には手におえないのでここに出しました。
問題1に関しては教科書を見れば載っているだろうと思い軽く考えていたのですが、
問題2は一筋縄では行かないだろうと思っていました。
N=5の時について、私も調べますので頑張りましょう。
◆愛知県 Y.M.Ojisan さんからのコメント。
N=5 に関し、剰余類でのふるい落としを試みましたが、、C=P2とするとき
4の剰余類検査の場合に P=1,3 mod 4 が排除される以外は良い結果が得られませんでした。
なお 引き続き P=24、26、28、30、32で存在しないことを確認しました。
◆愛知県 Y.M.Ojisan さんからの解答。
【問題2解答追加】
(I)ANからA2N+1を作成する
N=2k-1から, N=2k+1-1を作成した方法を拡張して
ANからA2N+1を作成する方法を示し、可能な範囲を広げます。
【C=P2の場合】
ANT*AN=P2*(N*IN-DN) ----(2’)
ここで P:自然数その他(2)に同じ
が成立しているとき、2N+1×2N+1の行列を次のように作ります。
なおSNSNt=IN+DNです。
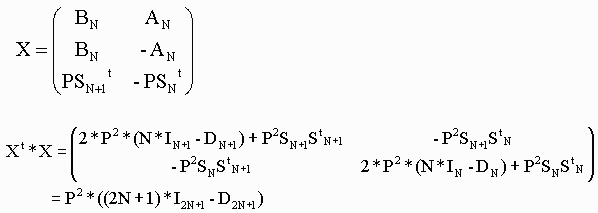
従って、Xは(2)の条件を満足す行列です。
以上から 2k−1以外にN=9やN=11を始めとして
N=10*2k−1, N=12*2k−1
すなわち、9、19、39,79,...や11、23、47、95,...も可能であることが分かります。
【C=2P2の場合】
ANT*AN=2P2*(N*IN-DN) ----(2’)
ここで P:自然数その他(2)に同じ
が成立しているとき、2N+1×2N+1の行列を次のように作ります。
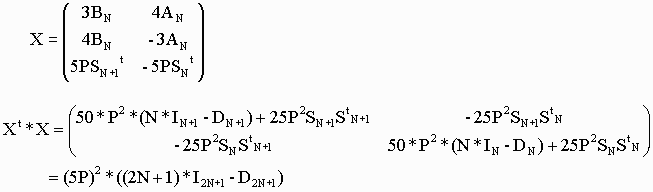
従って、Xは(2)の条件を満足す行列で C=P2のタイプです。
以上から N=8を始めとしてN=9*2k−1、
すなわち、8、17、35、71,...も可能であることが分かります。
【その他C=TP2の場合】
T=1 の場合を (1、1、P)
T=2 の場合を (3、4、5P)
であらわすとき
T=10: (1、2、5P)
T=20: (1、3、10P)
T=26: (2、3、13P)
等があります。
(II) ANからA10N+9 A9N+8 を作成する
a×b行列 R と c×d 行列 E があって
Rの要素をE倍(スカラー倍)したac×bd行列 Qを造る操作を
R♀Eで表記します。
具体的には {R♀E}i*c+j,k*d+l=Ri,k*Ej,lです。
また、 (2)式はBNT*BN=C*(N*IN+1-DN+1) ----(2’’’)
と等価です。
L×L行列 R が Rt*R=L*ILであり
QがT*P2系で(2)を満たすもののB型(2’’’式)であるとき、
T*P2系のANから得られたBNを元に作成した次の行列は
(2)を満足するT*P2系の行列(BLN+L-1)です。
したがって、一般に (N+1)Lk−1の系列が作成可能になります。
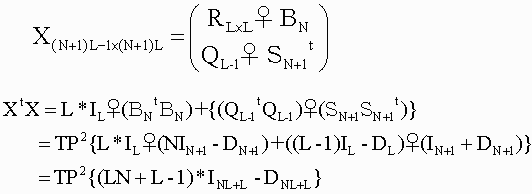
具体的には(R、Q)としてすくなくとも下図の2組(L=10,T=1系とL=9、T=2系)がありました。従って
2*10k−1=1、19、199、1999
4*10k−1=3、39、399、3999
8*10k−1=7、79、799、7999
10*10k−1=9、99、999、9999
12*10k−1=11、119、1199、11999
16*10k−1=15、159、1599、15999
や
9*9k−1=8、80、728、6560
が可能です。
【R10×10】
Qは先に示したC=1のB9を用いて Q=P*B9とする。
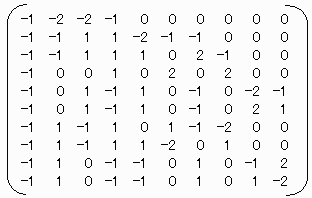
【R9×9】
Qは先に示したC=2のB8を用いて Q=P*B8とする。
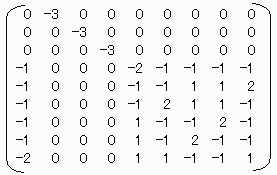
◆埼玉県 \aleph_0 さんからの解答。
【問題2解答】
Y.M.Ojisan氏の結果を含め,解答をレポートの形にまとめてみました.
(青木注:上位互換バージョン(PDFファイル)がでたので、削除しました。)
ただし,記述を簡単にするためにnが一つずれているのでご注意ください.
また,趣味で文字や記号も多少(かなり?)変えましたがご了承ください.
なお,定理1および命題2はY.M.Ojisan氏の結果を書き直したものです.
謝辞:この問題の面白さを教えてくださったY.M.Ojisan氏に感謝します.
◆愛知県 Y.M.Ojisan さんからの解答。
【問題2解答追加2】
N+1が平方数のとき作成可能で、それはC=P2タイプである。
∵ A0点を(-1,-1,-1,・・・-1)t に固定し、AI点をI成分のみXであるとする。
AI=(0,0,・・・X,・・・0)t
このときAIとAJ (I>0,J>0)間の距離2は2X2で、
A0とAJ (J>0) )間の距離2はX2+2X+Nである。
以上から N=X2-2X=(X-1) 2-1が得られる。
即ちNが平方数−1であるとき存在する。
| 重心は | X-1 N+1 | *{ 1,1,1,・・・,1} tであるから |
| N*( | X-1 N+1 | +1) | 2 | = | N*X2 (X-1)2 | である。 |
以上から N=3、8、15、24、35、48、が可能であることが分かった。
特にN=8のC=P2タイプが存在するので 9N+8倍の創生や8を種にした創生も可能である。
先の結果とまとめると、Nが偶数の場合は 平方数−1のとき存在し、それ以外では存在しないことが確定した。
【PS】
(1)以上を書いたところで \aleph_0さんの美しい論文が発表されました。
今回の解答は\aleph_0定理3と同じ内容なのですが、思考過程が見えるので良いかなと思い、提出しました。
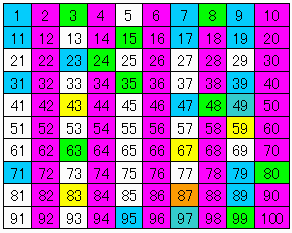
(2)さて、\aleph_0さんの定理と合わせて100までをチェックすると下図です。
まだまだ白いところがあります。
紫:命題2で存在しない。
青:存在する。
緑:定理3で存在。
黄色:定理5で存在。
橙色:定理4で存在。
白:不明。
(注記:記述順優先で色付けしてあり、重複して見えないのが多数あります。)
(3)頂点の一つを原点とした場合
tFN*FN=s{IN+UN}
s={N+1の奇数冪因数の積}*P2
という方程式も出てきます。
FN*AN=Z*IN という関係もあり、双対空間での議論の展開があるかも。
Uは全要素1の行列。
◆埼玉県 \aleph_0 さんからの解答。
【問題2解答】
前回の解答の続報です.
(PDFファイル)
![]()
"I"を別の意味で使ったため単位行列は"E"になっているのでご注意ください.
n∈Sとなるための十分条件は前回よりかなり広がりました.
一方,必要条件も命題3, 6, 7の場合で尽くされていると予想はされますが,
証明は難しそうです.
特にn=6(5次元)の場合を早く解決したいですね.
◆埼玉県 \aleph_0 さんからの解答。
懸案のn=6(5次元)の場合が解決できたと思います.
PDFファイル
方針は,定理4のrを割り切る2の巾に関する無限降下法です.
したがって,mod 2やmod 4での議論を多用しています.
内容は大したことをしていないのですが,
場合分けが多い上に説明が下手なのでやたらと長いです.:)
n≡6 (mod 8)の場合に拡張できるといいのですが,このままではとても通用しなさそうです.
というわけで,ご質問,ご指摘,歓迎です.
◆愛知県 Y.M.Ojisan さんからのコメント。
おめでとうございます。
5次元がわかれば一気に解決とはいかなかったのは残念です。
縮小(祝勝)行列 A/4の発見が味噌ですね。
頂点の一つを原点とした場合の
Ft5F5=C(I5+U5)=3P2(2I5+2U5)を用いれば
fi*fi≡0 (mod 4)
fi*fj≡0 (mod 2) i≠j
であること、および A/4 の固有値=0.5 で矛盾を言えばさらに簡素化できそうです。