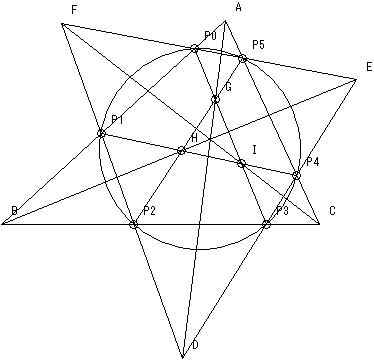
【問題】
△ABCが円と6個の交点で交わっている。
△ABCをA→B→C→Aと辿ったときに出会う順に、
これら6個の交点をP0〜P5とし、
P1P2とP3P4の交点をD、
P3P4とP5P0の交点をE、
P5P0とP1P2の交点をF、
P0P3とP2P5の交点をG、
P2P5とP4P1の交点をH、
P4P1とP0P3の交点をI とする。
AとGとD、BとHとE、CとIとFの3点3組がそれぞれ一直線上にあり、
かつそれらの3直線が1点で交わることを示せ。

【コメント】
成り立つことは作図ソフトで確認してありますが、出題者自身まだ解けていません。
【追加問題1】
3直線AD、BE、CFの交点をMとする。
六角形P0P1P2P3P4P5の隣り合う2頂点とMを通る円は6個存在するが、これら6円のうち1個跳びで隣り合う2円の交点は3直線AD、BE、CF上に存在することを示せ。
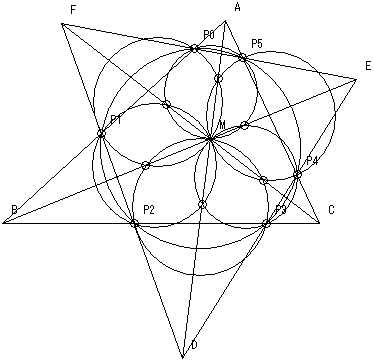
【追加問題2】
最初に与えられた円と3直線AD、BE、CFとの交点は6個存在するが、これら6点での接線に関するブリアンション点はMに一致することを示せ。
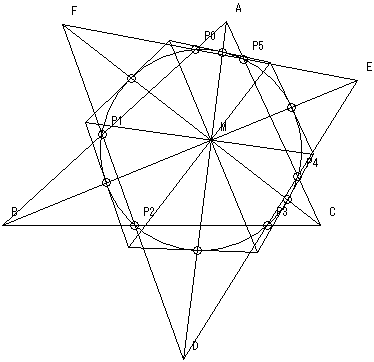
備考:ブリアンション(Brianchon)の定理
一つの円錐曲線に接する六つの接線により構成された六角形がABCDEFだとすると、直線AD、BE、CFは一点で交わる。
(フリー百科事典『ウィキペディア(Wikipedia)』より)
本問ではこの交点を(一般的な呼称かはわからないが)ブリアンション点と呼ぶ。
◆図形問題へもどる
 数学の部屋へもどる
数学の部屋へもどる