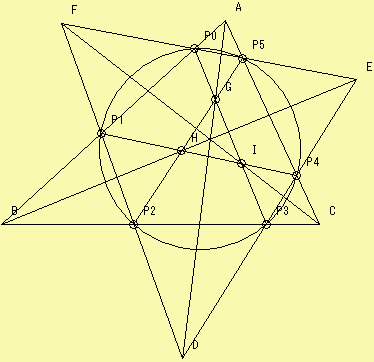
◆愛知県 Y.M.Ojisan さんからの解答。
【方針】
P0〜P5を先に与えれば、以降は直線の交点の計算(線形計算)のみですから、腕力で証明が可能です。
ここでは、円の中心を原点とする複素数平面で考え、これをMaxima(数式処理ソフト/Free)で解くこととします。
以降では、大文字記号(点の名前)は複素数、小文字は実数とします。

一般性を失わず円の半径を1とします。
このとき円上の6点Piは次の性質を持ちます。
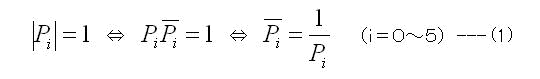
単位円上の任意の4点を、U,V,Y,Z とし、直線UV と直線YZ の交点をX とします。
このとき、X は下記で与えられます。
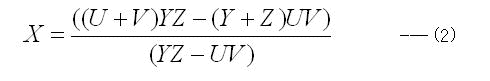
![]()
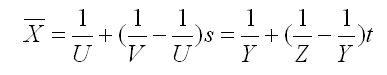
![テキスト ボックス: (C2) EQ1 : X = (V - U) s + U
(D2) X = s (V - U) + U
(C3) EQ2 : X = (Z - Y) t + Y
(D3) X = t (Z - Y) + Y
1 1 1 1 1 1
(C4) EQ3 : (- - -) s + - = (- - -) t + -
V U U Z Y Y
1 1 1 1 1 1
(D4) s (- - -) + - = t (- - -) + -
V U U Z Y Y
(C5) S1 : SOLVE([EQ1, EQ2, EQ3], [s, t, X])
2 2
V (Y Z + U (- Z - Y) + U ) V (U Z - Y Z) + Y Z - U Y Z
(D5) [[s = - -----------------------------, t = ----------------------------,
2 2 2 2
V (- Y Z - U ) + U Y Z + U V - Y Z + U V (Z - Y) + Y Z
V (U (Z + Y) - Y Z) - U Y Z
X = ---------------------------]]
U V - Y Z
(C6) X : FACTOR(RHS((S1 ) ))
1 3
V Y Z + U Y Z - U V Z - U V Y
(D6) -----------------------------
Y Z - U V
(C7) fX(Ua, Va, Ya, Za) := EV(X, [U = Ua, V = Va, Y = Ya, Z = Za])
(D7) fX(Ua, Va, Ya, Za) := EV(X, [U = Ua, V = Va, Y = Ya, Z = Za])
(C8) fX(U, V, Y, Z)
V Y Z + U Y Z - U V Z - U V Y
(D8) -----------------------------
Y Z - U V](img6b/image015.gif)
対称なのでBHE の場合のみ示します。
方針はHB//HE を複素数的に、下記が成立することで示します。
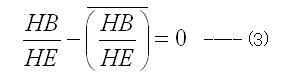
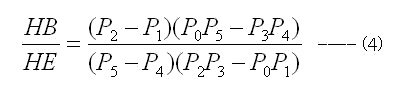
![テキスト ボックス: fX(P0, P1, P2, P3) - fX(P1, P4, P2, P5)
(C9) HBbyHE : FACTOR(---------------------------------------)
fX(P0, P5, P3, P4) - fX(P1, P4, P2, P5)
(P2 - P1) (P0 P5 - P3 P4)
(D9) -------------------------
(P2 P3 - P0 P1) (P5 - P4)
(C10) fHBbyHE(P0a, P1a, P2a, P3a, P4a, P5a) :=
EV(HBbyHE, [P0a = P0, P1a = P1, P2a = P2, P3a = P3, P4a = P4, P5a = P5])
・・・
1 1 1 1 1 1
(C12) FACTOR(fHBbyHE(P0, P1, P2, P3, P4, P5) - fHBbyHE(--, --, --, --, --, --))
P0 P1 P2 P3 P4 P5
(D12) 0](img6b/image020.gif)
直線CFと直線ADの交点Mの値を求めると、(5)式であり、
(P0,P1,P2,P3,P4,P5)に対して円環状に対称な式である。
即ち3直線CF,AD,BE は一点で交差する。
∵ 交点M は下記の方程式の解である。
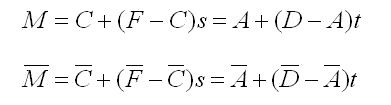
これをとけば(5)式が得られる。
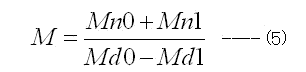
ここで
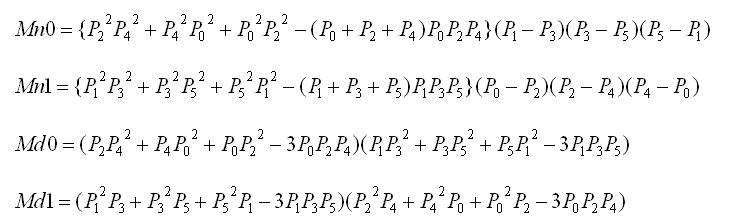
である。

このように綺麗な関係があるとは知りませんでした。
幾何でエレガントに解くべきであり、邪道かもしれませんが嗜好により計算機による解法を考えました。
なお、Maxima Primerはインタフェースが旧式ですが、フリーの使える数式処理ソフトです。
◆出題者のコメント。
Y.M.Ojisan さん、解答ありがとうございます。
私もベクトルを使って証明できないかと少しだけ試してみていたのですが、手計算だったため Y.M.Ojisan さんの解答のXを求める段階で早くも挫折していました…。
実際、解答を見る限り手計算ではちょっと難しそうですね。
結局幾何で試行錯誤していたのですが、六角形と3直線との6個の交点に関する特徴を見つけだせず、私は未だに証明には至っていません。
引き続き幾何による解答もお待ちしています。
なお、出題後の試行錯誤の間に見つけた関係を追加問題にしたいと思います。
作図ソフトで確認しただけで出題者自身が解けていない問題ばかりですが、ご容赦下さい。
【追加問題1】
3直線AD、BE、CFの交点をMとする。
六角形P0P1P2P3P4P5の隣り合う2頂点とMを通る円は6個存在するが、これら6円のうち1個跳びで隣り合う2円の交点は3直線AD、BE、CF上に存在することを示せ。
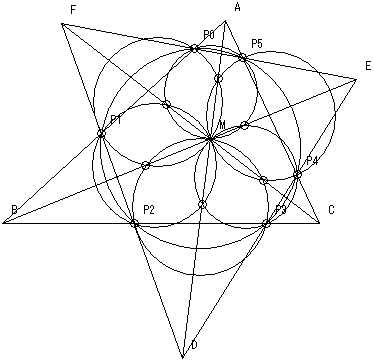
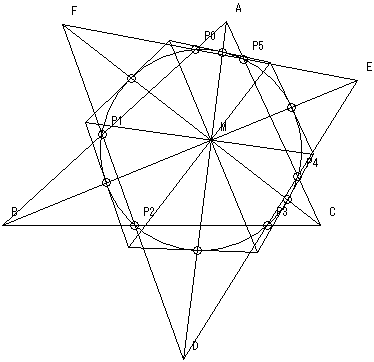
【追加問題2】
最初に与えられた円と3直線AD、BE、CFとの交点は6個存在するが、これら6点での接線に関するブリアンション点はMに一致することを示せ。
備考:ブリアンション(Brianchon)の定理
一つの円錐曲線に接する六つの接線により構成された六角形がABCDEFだとすると、直線AD、BE、CFは一点で交わる。
(フリー百科事典『ウィキペディア(Wikipedia)』より)
本問ではこの交点を(一般的な呼称かはわからないが)ブリアンション点と呼ぶ。
◆神奈川県の高校生 omega さんからの解答。
【問題】
P0P1P2P5P4P3に関するパスカルの定理より、A,G,Dは1直線上にある。
同様に、B,H,E、C,I,Fもそれぞれ1直線上にある。
また、P0P1P2P3P4P5に関するパスカルの定理より、BCとEFの交点、CAとFDの交点、ABとDEの交点は1直線上にあるので、デザルグの定理の逆により、AD,BE,CFは1点で交わる。
【追加問題1】
円P0P1P2P3P4P5に関する方ベキの定理より、
AP0・AP1=AP4・AP5。
つまり、Aの円P0P1Mに対する方ベキとAの円P4P5Mに対する方ベキが等しいので、Aはこの2円の根軸上にある。
よって、この2円の2つの交点とAは同一直線上にある。
ほかの点に対しても同様。
◆神奈川県 クラテス さんからの解答。
都合により、【問題】を前半部(A,G,D等が一直線上)と後半部(3直線が1点で交わる)に分けます。
証明順は【問題(前半)】→【追加問題1】→【追加問題2】→【問題(後半)】です。
【問題(前半)】
図1のように必要な部分だけを抜き出す。
AGの延長とP1P2及びP3P4の交点をJ,Kとする。
また3点A,P0,P5を通る円を描き、AGとの交点をLとする。
∠P5LA=∠P5P0A(円周角)
∠P5P0A=∠P1P2P5(円内四辺形)
だから、∠P5LA=∠P1P2P5となり、
結局∠GLP5=∠GP2Jとなります。
また、∠P5GL=∠JGP2(対頂角)だから、
結局△GLP5と△GP2Jは相似な三角形となります。
よって、P5G*GP2=LG*GJ ・・・1
同様にして△GLP0と△GP3Kも相似な三角形となるから、
P0G*GP3=LG*GK ・・・2
1,2よりP5G*GP2=P0G*GP3であるから
(四角形P0P2P3P5は円内四辺形)、
結局 LG*GJ=LG*GKとなり、これはJとKが一致することを示す。
つまりAGの延長はP1P2とP4P3の延長の交点Dで交わる。
他も同様である(証明終)。
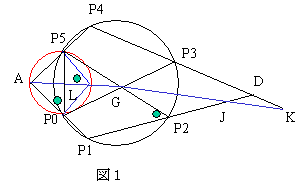
【追加問題1】
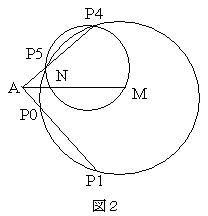
図2のように必要な部分だけを抜き出す。
AMと円MP4P5との交点のうちMでないものをNとする。
方べきの定理より、
AP5*AP4=AN*AM ・・・3
同様に方べきの定理より
AP5*AP4=AP0*AP1 ・・・4
3,4よりAN*AM=AP0*AP1となるから、
結局4点P0,P1,N,Mは同一円周上の点である(方べきの定理の逆)。
よってM,P0,P1を通る円とM,P4,P5を通る円はAM上つまりAD上で交わる
(まだMがAD,BE,CFの交点であることは示せていないが、この問題ではMは実はAD上の点ならどこでもよい)。
【追加問題2】
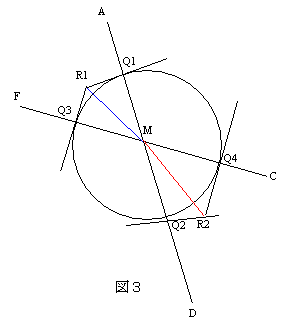
図3のように必要な部分を抜き出す。
AD、FCと円との交点をQ1,Q2,Q3,Q4とする。
Q1,Q3における接線の交点をR1,Q2,Q4における接線の交点をR2とする。
Q1Q2とQ3Q4の交点は明らかにMであり、
R1Mは∠Q1MQ3をR2Mは∠Q2MQ4を明らかに二等分するから、R1,M,R2は1直線上である。
他も同様に考えて、結局6本の接線によって作られる6角形のブリアンション点はMに一致する。
結局【問題(後半)】が解ければよいことになります。
ですから【追加問題】は双方とも付録のような問題です。
【問題(後半)】
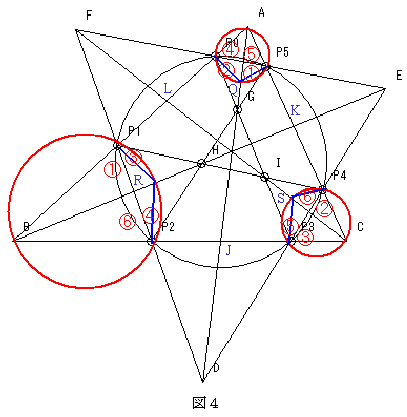
図4のように説明しやすいように記号をつける(図は拝借)。
ADとBC、BEとCA、CFとABの交点をJ,K,Lとし、円AP0P5とADの交点をQ、円BP1P2とBEの交点をR、円CP3P4とCFの交点をSとする。
| BJ JC |
= | △ABQ △ACQ | = | AB*QP0 CA*QP5 |
・・・(A) |
| CK KA |
= | BC*RP2 AB*RP1 |
・・・(B) |
| AL LB |
= | CA*SP4 BC*SP3 |
・・・(C) |
| BJ BC | * | CK KA | * | AL LB |
| = | AB*QP0 CA*QP5 | * | BC*RP2 AB*RP1 | * | CA*SP4 BC*SP3 |
| = | QP0 QP5 | * | RP2 RP1 | * | SP4 SP3 | ・・・(D) |
| QP0 QP5 | は明らかに | sin∠P0AQ sin∠P5AQ | に等しい。 |
| = | 1 2 | *AG*AP0*sin∠P0AQ |
| = | 1 2 | *AP0*GP0*sin(π-(6)) |
| = | 1 2 | *AP0*GP0*sin(6) |
| = | 1 2 | *AG*AP5*sin∠P5AQ |
| = | 1 2 | *AP5*GP5*sin(π-(3)) |
| = | 1 2 | *AP5*GP5*sin(3) |
| であり、 | GP0 GP5 | = | sin(1) sin(2) | だから |
| sin∠P0AQ sin∠P5AQ |
| = | GP0*sin(6)/AG GP5*sin(3)/AG |
| = | sin(1)*sin(6) sin(2)* sin(3) | ・・・(E) |
| 結局 | QP0 QP5 | = | sin(1)*sin(6) sin(2)* sin(3) |
が成立する。 |
| RP2 RP1 | = | sin(2)* sin(3) sin(4)*sin(5) |
| SP4 SP3 | = | sin(4)*sin(5) sin(1)*sin(6) |
| BJ JC |
* | CK KA | * | AL LB |
= 1が成立する。 |
◆出題者のコメント。
幾何による解答ありがとうございます。
私自身諦め掛けていたので、お二方から同時に解答があり驚きました。
omegaさん
どちらも非常にエレガントな解答ですね。
最初の問題はパスカルの定理を適用するときの点の順序を変えるだけで良かったとは気づきませんでした。
目から鱗でした。
クラテスさん
【問題(前半)】は結局パスカルの定理を証明したのと同じことですね。
ちなみに同じ補助円を使った別証明が「ヨッシーの算数・数学の部屋」さんの「定理の覚え書き」にありました。
今回の問題に当てはめると以下のようになります。
「円AP0P5とP0P3のP0以外の交点をK、円AP0P5とP2P5のP5以外の交点をLとしたとき、
△DP3P2と△AKLが相似になるため、AD、P0P3、P2P5は1点Gで交わる。」
【追加問題1】は基本的にomegaさんと同様の考え方ですね。
【追加問題2】は残念ながら間違っています。
Mは円の中心ではないので、R1MやR2Mは∠Q1MQ3や∠Q2MQ4を2等分しません。
【問題(後半)】はおそらくチェバの定理の逆を使うという方針を決めて出発していると思うのですが、
辺の比を角度の比に置き換えていく過程がうまいですね。