『等間隔の並び』

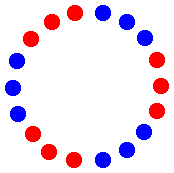
【問題】

以下、あいだに存在する玉数が等しいことを「等間隔」と呼ぶものとします。
また、「ｎ個が等間隔に並ぶ」とは、ｎ個が存在する弧(円周ではない)の上で等間隔である意味です。

【問題１】

赤玉,青玉合せて９個を、１つの円周上に置くものとします。
ある同色の玉３個は、必ず等間隔に並ぶことを示してください。

【問題２】

赤玉と青玉のいくつかを、１つの円周上に置くものとします。
「同色の玉ｎ(≧３)個が等間隔に並ぶ」ことが許されないときの、円周上に存在できる玉の最多数をLess(ｎ)とします。

Less(ｎ)を求め、その証明をしてください。

ちなみに、【問題１】からも分かるように、Less(３)＝８です。

◆出題者のコメント(ヒント)

３ヶ月以上も無回答なので、ヒントを出します。

ｎ＝４なら、次のように並べても同色の玉４個は等間隔になりません。

ですから、Less(４)≧１８であることは判ります。

一般に、Less(ｎ)≧２(ｎ－１)² であることも同様に判ります。
はたして、２(ｎ－１)² 個が、同色ｎ個が円弧上で等間隔とならない玉数の最多なのか？
それとも、２(ｎ－１)² 個よりも多い玉数でも可能なのか？
そこが問題です。
（ただし、ｎは３以上の整数。）