
仧垽抦導丂Y.M.Ojisan 偝傫偐傜偺夝摎丅
亂栤戣侾亃
俁屄楢懕偱暲傇偙偲偼偱偒側偄偺偱侾屄傑偨偼俀屄楢懕偱怓偑岎戙偟傑偡丅
慡晹偱俋屄乮婏悢乯側偺偱侾屄偽偐傝偲偄偆傢偗偵偼備偐偢丄彮側偔偲傕侾売強俀屄乮BC乯偺偲偙傠偑偁傝傑偡丅
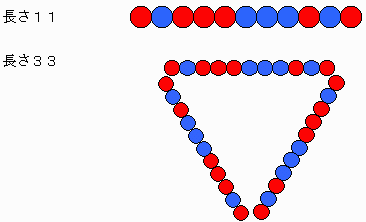
偙傟傜傪壓恾乮侾乯偺傛偆偵俀丆俁偺偲偙傠偵偍偒傑偡丅
侾丄係偺埵抲(A)丆乮D乯偼暿偺怓偱側偗傟偽側傝傑偣傫丅
偡傞偲偝傜偵俁屄摍娫妘乮廲墶幬傔乯偵暲偽側偄傛偆偵 俈丆俆丆俋丆俉偺埵抲偺怓偑昁慠揑偵寛傑傝傑偡乮俀乯丅
偙傟傛傝俇偺埵抲偵偍偔怓偑側偔側傝傑偡丅
傛偭偰昁偢俁屄摍娫妘偵暲傃傑偡丅

亂栤戣俀亃
値=係偺応崌偵丂師偺傛偆偵挿偝偑慺悢偱偁傞侾侾偺嫮偄夝乮懚嵼斖埻傪墌屖偵尷傜偢壗廃偟偰傕傛偄偲偟偨忦審壓偺夝乯偑偁傞偺偱丄
偦偺俁攞乮=n-1攞)攞偺夝偑懚嵼偟偰Less(4)亞33丂偱偁傞偙偲偑傢偐傝傑偡丅
崱夞偺僸儞僩傪摼偰傕偙偺愭偑丠偱堦斒夝偼崀嶲偱偡丅
仧嶰廳導丂捁嫃丂懽怢 偝傫偐傜偺夝摎丅
亂栤戣侾亃
n亖3 偺偲偒丄摨偠怓偺嬍偼侾屄傑偨偼俀屄楢懕偵尷傜傟傞丅
傕偟摨怓俀屄楢懕偺暲傃偑側偄偲偡傟偽丄愒嬍偲惵嬍偼岎屳偵暲傇偙偲偵側傝丄慡懱偺嬍偺屄悢偼嵟戝係屄偱偁傞丅
乮慡懱偺嬍偺屄悢偑俆屄埲忋偵側傞偲丄娫妘俀偺摨怓俁屄偺摍娫妘暲傃偑偱偒傞丅乯
摨怓俀屄楢懕偺暲傃偑偁傞応崌丄偦偺椉抂偼暿偺怓偺嬍偑偔傞偺偱丄仠仜仜仠偲偄偆暲傃偑偱偒傞丅
偙偺係屄偺暲傃偺師偵壗怓偺嬍傪攝抲偡傞偙偲偑偱偒傞偐傪庽宍恾偱昞偡偙偲偵偡傞丅
偳偪傜偺嬍傕攝抲偱偒側偔側偭偨偲偙傠傪亊偱昞偡丅
仠劅仜劅仜劅仠劍仜劍仜劅亊丂(1) 丂丂丂丂丂丂丂劆丂劋仠劅亊丂(2) 丂丂丂丂丂丂丂劋仠劅仜劅仜劅仠劅亊丂(3)偙偺偆偪(1),(2)偼丄亊偺偲偙傠偵巒揰傪傕偭偰偒偰椫偺宍偵偡傞偲丄巒揰偐傜巒傑傝亊偱廔傢傞俁屄偺摍娫妘乮娫妘俁乯偺暲傃偼埖傢側偔偰傛偄偙偲偵側傞丅
廬偭偰丄Less(3)亖8
亂栤戣俀亃
堦斒夝偲偄偆夝偒曽偼偱偒側偐偭偨偺偱丄屄暿偺 n 偵偮偄偰摼傜傟偨寢壥傪帵偡丅
亙夝朄侾亜
n亞4 偺偲偒丄忋偵帵偟偨庽宍恾幃偵夝傪媮傔偰傒偨丅
僐儞僺儏乕僞傪巊偭偰丄n亖4,5 偺偲偒埲壓偺夝傪摼偨丅
Less(4)亖33
乮仜仜仜仠仜仜仠仜仠仠仠乯亊俁
Less(5)亖176
乮仜仠仠仠仜仠仜仜仠仜仜仜仜仠仜仜仠仜仠仠仠仜仠仜仜仜仠仜仠仠仜仠仠仠仠仜仠仠仜仠仜仜仜仠乯亊係
亊俁丆亊係偼丄奺乮丂乯撪偺暲傃傪俁丆係夞孞傝曉偟偰椫傪嶌傞偙偲傪堄枴偡傞丅
側偍丄忋偵帵偟偨夝偼堦椺偱偁傝丄懠偺夝傕偁傞丅
乮昁偢偟傕孞傝曉偟偲側傜側偄夝傕偁傞丅乯
亙夝朄俀亜
埲壓偺俀偮偺栤戣傪峫嶡偡傞丅
嘥丗擟堄偵慖傫偩 n 屄偺摍娫妘偺暲傃偺拞偵丄昁偢俀庬椶偺怓偺嬍偑偁傞丅偙偙偱丄摍娫妘偺暲傃偺 n 屄偼摨偠嬍傪嫟桳偡傞偙偲傪擣傔側偄丅
嘦丗擟堄偵慖傫偩 n 屄偺摍娫妘偺暲傃偺拞偵丄昁偢俀庬椶偺怓偺嬍偑偁傞丅偙偙偱丄摍娫妘偺暲傃偺 n 屄偼摨偠嬍傪嫟桳偟偰傕傛偄丅
杮栤偼嘥傪枮偨偣偽廫暘偱偁傞丅
m 屄偺嬍偐傜側傞暲傃偵偍偄偰嘦偑惉棫偡傞偲偒丄偦偺夝傪 n-1 夞孞傝曉偟偰墌宍偵暲傋偰偱偒傞丄慡懱偱 m(n-1) 屄偺嬍偐傜側傞丄嘥偺夝偑摼傜傟傞丅
乵徹柧乶
嘦傪枮偨偡夝傪 n-1 夞孞傝曉偟偰偱偒傞 m(n-1) 屄偺嬍偐傜側傞墌宍偺暲傃偵嬍偺斣崋傪怳傞丅
偝偰丄i 斣栚偐傜 d 偢偮恑傫偱 n 屄偺嬍傪庢傝弌偡偲丄偦偺斣崋偼 i,i+d,...,i+d(n-1) 偱偁傞丅
偙偙偱慖傃弌偟偨 n 屄偑嘥傪枮偨偡偨傔偵偼丄彮側偔偲傕 d 偼 m 偺攞悢偱偼側偄丅
乮d 偑 m 偺攞悢偲偡傞偲丄d(n-1) 偼 m(n-1) 偺攞悢偲側傝丄i 偲 i+d(n-1) 偼摨偠嬍傪帵偡偙偲偵側傞丅乯
d 偑 m 偺攞悢偱側偗傟偽丄嘦偑惉棫偡傞偙偲偵側傝丄i,i+d,...,i+d(n-1) 斣栚偺嬍 n 屄偵偼俀庬椶偺怓偑偁傞丅
埲忋傛傝丄摨偠嬍傪嫟桳偟側偗傟偽丄n 屄偺摍娫妘偺暲傃偵偼俀庬椶偺怓偑偁傝丄嘥偑惉棫偡傞丅仩
n亖6 偵偮偄偰丄嘦偺夝傪僐儞僺儏乕僞傪巊偭偰媮傔偨丅
偦偙偐傜摼傜傟偨杮栤偺夝偺堦椺偼埲壓偺傛偆偵側偭偨丅
Less(6)亞1130
乮仜仜仠仠仜仠仜仠仠仜仠仜仜仜仠仠仠仜仠仜仜仜仠仜仜仠仜仜仜仜仜仠仠仜仜仜仠仜仜仜仜仠仜仠仠仠仠仠仜仠仠仜仜仜仜仠仠仠仜仜仜仜仠仠仜仠仠仠仠仠仜仠仜仜仜仜仠仜仜仜仠仠仜仜仜仜仜仠仜仜仠仜仜仜仠仜仠仠仠仜仜仜仠仜仠仠仜仠仜仠仠仜仜仠仠仜仜仠仜仠仜仜仠仜仠仠仠仜仜仜仠仜仠仠仠仜仠仠仜仠仠仠仠仠仜仜仠仠仠仜仠仠仠仠仜仠仜仜仜仜仜仠仜仜仠仠仠仠仜仜仜仠仠仠仠仜仜仠仜仜仜仜仜仠仜仠仠仠仠仜仠仠仠仜仜仠仠仠仠仠仜仠仠仜仠仠仠仜仠仜仜仜仠仠仠仜仠仜仜仠仜仠仜仜仠仠乯亊俆
忋偱帵偟偨 Less(6) 偵晄摍崋偑偮偄偰偄傞偺偼丄嘦偺夝偺拞偱嵟戝偺 m 傪梌偊傞傕偺偐徹柧偱偒偰偄側偄偙偲丄嘦偺夝傪俆夞暲傋偨傕偺偑嘥偵偍偄偰嵟戝偺嬍悢偲側傞夝偵側偭偰偄傞偐徹柧偱偒偰偄側偄偙偲偵傛傞丅
n亞7 偵偮偄偰偼丄僐儞僺儏乕僞偺寁嶼尷奅偵傛傝丄妋偐側昡壙偑偱偒偰偍傝傑偣傫丅