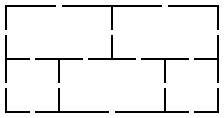
この建物のすべての出入り口を1度ずつ通るのは不可能であることを示せ。
できるだけ多くの人に納得してもらえる、単純明快な証明を求めます。
([単純明快な証明]とは、[短い証明]という意味ではありません。)
【問題1】
ある建物には、図のように5個の部屋と16個の出入り口がある。
この建物のすべての出入り口を1度ずつ通るのは不可能であることを示せ。
【問題2】
鈍角三角形の鈍角の対辺上の任意な点をPとする。
Pより出発し他の2辺に蝕れて再びPに戻る最短閉路は、
「Pと鈍角である頂点とを結ぶ線分の往復路」であることを示せ。
【問題3】
n(≧3)個の整数の中には、和または差が、
2の倍数となる2数 ,
3の倍数となる2数 ,
… ,
(2nー3)の倍数となる2数
が必ず存在することを示せ。
(もちろん、0はすべての整数の倍数。)
 数学の部屋へもどる
数学の部屋へもどる