◆神奈川県 蟻 さんからの解答。
【問題3】
n個の整数をa1,a2,…,anとおく。
k∈{2,3,…,2n−3}を1つ固定し、
整数mに対してf(m)=(mをkで割った余り)とおき、
| m'=f(m) (if 0≦f(m)≦[ | k 2 | ]),k−f(m) (if [ | k 2 | ]<f(m)≦k-1)とおく。 |
| このときm'∈{0,1,2,…,[ | k 2 | ]}:=Xが成り立つ…(i)。 |
次に、A={a'1,a'2,…,a'n}とおく。
Aのどの元も重複していないとすると、|A|=nである。
また、(i)からA⊂Xである。
よって特に|A|≦|X|である。
| しかし、|A|=n=[ | 2n−3 2 | ]+2≧[ | k 2 | ]+2>[ | k 2 | ]+1=|X|なので矛盾。 |
よって、Aの元のうち、重複しているものがある。
すると、あるs,t(s≠t)が存在してa's=a'tが成り立つ。
このとき、(ii)から±as≡±at (mod k)
よって、as+at≡0 (mod k)またはas−at≡0 (mod k)が成り立つので、題意は示された。
◆東京都 ぽこぺん さんからの解答。
【問題1】
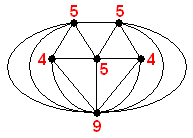
建物の外部および各部屋の中に頂点を取り,部屋と部屋(部屋と外部)とが出入り口を通じて
直接出入り可能なときに頂点同士を辺で結ぶことにすると,問題の図に対応して次図のグラフが得られる。
建物のすべての出入り口を1度ずつ通る経路は,このグラフのオイラー路に対応する。

ここで,各頂点の次数 (頂点から発する辺の数) はグラフ中に赤で示すとおりであり,
奇数次の頂点が 4 個ある。
したがって,オイラーの定理によりオイラー路は存在しない。
【問題2】
鈍角三角形 ABC において,A を鈍角の頂点とし,直線 AB に関して点 C と対称な位置に点 C' を取る。
ここで,辺 BC 上の点 P と対称な点を P' とすると,P より出発し他の 2 辺に蝕れて再び P に戻る最短閉路を求める問題は,P より出発し,辺 AC' に触れて P' に至る最短経路 (この経路は必ず AB を横切る) を求める問題に対応する。
さらに,これは △ABC と △ABC' を合併した図形 F に含まれる折れ線の最短経路を考えれば十分である。

辺 AC' 上の点 R に対して,線分 PR,RP' がどちらも F に含まれている場合は,
下図の P1-R1-P1' のように
P1R1 + R1P1' ≧ P1A + AP1' が成立する。
(∵ A における AB の垂線に関してAB と AC' とは反対側にある)
含まれていない場合は,下図の P2-Q2(=A)-R2-P2' のよう
に,
P2A + AR2 + R2P2' ≧ P2A + AP2' が成立する。
(∵ △AR2P2' の 2 辺の和 と 1 辺)
以上,いずれにしても,P-A-P' が最短経路になるから,元の問題において題意が成立する。
【問題3】
与えられた n 個の整数の集合を S とする。
2 ≦ m ≦ 2n-3 なる m に対し,同値関係 〜 を
x 〜 y ⇔ x ± y ≡ 0 (mod m)
と定義し,〜 によって整数を分類すると,
| [ | m 2 | ]+1 個の互いに排他的な集合 |
| A | i | ={ a∈S | a〜i } (i = 0,…,[ | m 2 | ])が得られる |
| [ | m 2 | ]+1≦[ | 2n-3 2 | ]+1<nであるから, |