『証明問題一発勝負』

できるだけ多くの人に納得してもらえる、単純明快な証明を求めます。
([単純明快な証明]とは、[短い証明]という意味ではありません。)

【問題１】

(ｎ＋１)^k－１はｎで割り切れることを示せ。

ただし、ｎは正整数、ｋは非負整数とする。

【問題２】

奇数個の頂点を持ち、どの頂点にも奇数個の面が集る多面体は存在しないことを示せ。

【問題３】

互いに相異なる２進数が３個以上の任意個数あるとき、
これらの２進数を３進数と考えると、どんな３数であっても等差数列にならないことを示せ。

【問題４】

Ｐ² ＞１２を満たすどんな素数Ｐも、Ｐ²を１２で割ると１余ることを示せ。

【問題５】

(２ｎ＋１)チームの総当り戦では、どのチームもｎ勝ｎ敗になり得ることを示せ。

ただし、ｎは正整数とする。

以下、追加問題

【問題６】

命題Ｐ,Ｑ,Ｒがいずれも真ならば、[ 常に本当のことを言う人が必ず存在する。] は真であることを示せ。

【問題７】

直径以外の弦において、その中点(だけ)を通る弦は、元の弦よりも必ず長いことを示せ。

【問題８】

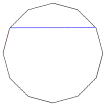
正１２角形と等しい面積を持つ正方形なら、正方形の１辺の長さは、その正１２角形の図のような対角線に等しいことを示せ。