◆愛知県 Y.M.Ojisan さんからの解答。
【問題1】
どれが分かりやすいでしょうか?
(1)k=0は成立している。
k>0のとき、与式はnのk次多項式である。
n=0とすると与式=0である。
よって与式=n*nのk-1次式である。
(2)k=0は成立している。
k=p-1の時成立しているとする。
(n+1)p-1=n*(n+1)p-1+(n+1)p-1-1はnの倍数である。
よって数学的帰納法により一般に成立。
(3)(1+n)kは1かnのいずれかを合計k個掛け合わせた項の和である。
そのうちnの倍数でないのは全部1を選んだ場合の1通りである。
よって、これを除いた(n+1)k-1はnの倍数である。
| (4)等比数列の公式 | k-1 Σ p=0 |
(1+n)p | = | (1+n)k-1 n | がある。 |
◆京都府 大空風成 さんからの解答。
【問題1】
f(n)=(n+1)k-1 とおくと、
f(0)=1k-1=0 だから、
因数定理より、
f(n) は n で割り切れる。
【問題2】
辺は面と面の間にあるから、
1つの頂点に集まる面の数と辺の数は等しい。
この多面体のどの頂点にも奇数個の面が集まるから、
辺も奇数個集まる。
それを奇数個のすべての頂点について加えた辺の「のべ個数」は、
奇数を奇数個集めたのだから、辺の「のべ個数」も奇数である。
ところが、辺は頂点と頂点の間に1つあるから、
この多面体の辺の数は、辺の「のべ個数」を2で割ると求められるが、
奇数を2で割ると整数ではないので、そのような多面体は存在しない。
【問題3】
3数 a、b、c がこの順に等差数列ならば、2b=a+c である。・・・(1)
題意の数は、各位の数が 0 か 1 であるが、
2倍すると、各位の数が 0 か 2 になる。
一方、異なる2数の同じ位について比較すると、
最低一箇所は 0 と 1 という異なる数の位をもつ。
よって、その2数の和を求めると、
必ず1である位が存在し、(1)をみたすことはない。
【問題4】
自然数は、
6n-1、6n、6n+1、6n+2、6n+3、6n+4
のいずれかである。
12以上の素数pは、2や3の倍数ではないから、
6n-1 か 6n+1 と表される。
p2=(6n±1)2
=36n2±12n+1
=12(3n2±n)+1
よって、 p2を12で割ると1余る。
【問題5】
(2n+1)チームを、同一円周上に等間隔に並べる。
どのチームについても、そのチームを通る円の直径より、そのチームから見て右側のチームには勝ち、左側のチームには負けたとする。
これに従うと、あるチームAは、Aを通る直径より右側のチームに勝ち、左側のチームに負けたので、n勝n敗となる。
Aが勝った相手チームのうちの1つをBとすると、Aは、Bを通る直径の、Bから見て左側なので、BはAに負けた。
つまり、AはBに勝ったことになるので、矛盾は起こらない。
よって、すべてのチームがこれをみたし、n勝n敗となる
◆長野県の高校生 MISERY さんからの解答。
【問題1】
以下 mod nとして
(n+1)k−1≡1k−1=1−1=0
(∵n+1≡1)
よって割り切れる。(q.e.d.)
【問題4】
5以上の全ての素数は、6n±1の形で表されることを示す。
(nは自然数)
5以上の全ての自然数は、
6n−1,6n,6n+1,6n+2,6n+3,6n+4
のいずれかで表される。
ここで、6n,6n+2,6n+3,6n+4は明らかに素数ではない。
よって、5以上の全ての素数は6n−1,または6n+1であらわされる。
(q.e.d.)
そして、P2>12を満たす素数Pは、5以上の全ての素数である。
だから、P=6n±1 とかけ、
P2=36n2±12n+1≡1 (mod12)
よって題意は示された。(q.e.d)
【問題5】
数学的帰納法で示す。
n=1のとき明らかに成り立つ。
n=kのとき成り立つと仮定する。
このとき、(2k+1)チームが総当り戦をしてどのチームもk勝k敗であるようにできる。
あらたに2つのチームA,Bを総当り戦に参戦させる。
まずAが自分とB以外の(2k+1)チームと勝負し、k+1勝k敗となり、
次にBも自分とA以外の(2k+1)チームと勝負し、
Aの勝ったチームには負けて、Aが負けたチームには勝つことによって、
k勝k+1敗となることは可能である。
そして最後にAとBが勝負をしてBが勝てば、
AとBは共にk+1勝k+1敗であり、
他の(2k+1)チームもk+1勝k+1敗となる。
よってn=kのとき成り立つならばn=k+1のときも成り立つ。
以上より数学的帰納法によって題意は示された。(q.e.d.)
◆千葉県 永山祐介 さんからの解答。
【問題1】
(n+1)k-1を二項展開すると、
| (n+1)k-1= | ( | k Σ i=0 |
kCink-i | )-1 |
(n+1)k-1
| = | ( | k Σ i=0 |
kCink-i | )-1 |
| = | ( | k-1 Σ i=0 |
kCink-i | ) +kCknk-k -1 |
| = | k-1 Σ i=0 |
kCink-i |
となる。これを nで割れば
| (n+1)k-1 n | = | 1 n |
k-1 Σ i=0 |
kCink-i | = | k-1 Σ i=0 |
kCink-i-1 |
i≦k-1なので nの係数k-i-1 は必ず0以上となる。
よって、(n+1)k-1は nで割り切れる。
【問題3】
問題を単純にするために、考える等差数列を単調増加のものに限る。
(単調減少の場合は順番を入れ替えればよいので問題ない)
相異なる二つの二進数を三進数と見た場合に、大きい方の数( a1とする)から小さい方の数( a0とする)を引いたものを xとする。
a0 とa1 の三進数表記
a0=(a0ma0m-1・・・・a01a00)3
a1=(a1na1n-1・・・・a11a10)3
の各桁について見た場合、違う値となる最右の桁 iについて考えると、 xの 桁目 xiは
a1i=0,a0i=1→ xi=2
a1i=1,a0i=0→xi=1
すると、同じ公差 xを持つ a2=a1+xのi 桁目 a2iは、
a2i=a1i+xi=2となり、必ず 2となる。
つまり、a0 とa1をどのようにとっても、 a2を0,1のみで表記することはできない。
よって、相異なる二進数を三進数と考えると、どんな3数であっても等差数列にならない。
【問題4】
p2>12 から、 pは5以上の素数である。
12=22・3 であるから、p と12 は互いに素。
よって、xp+12y=1となるような整数組(x,y) が存在する。
ここで上式の両辺を二乗し、法 12における値を考えると、
(xp+12y)2≡1(mod 12)
x2p2+24xyp+122y2≡1(mod 12)
x2p2≡1(mod 12)
となる。
ここで x2と p2は、積をとると1になることから、互いに逆数の関係にあることがわかる。
法 nの元である数 が逆数を持つのは、aとnが互いに素である場合だけであるから、法 12の元で逆数を持つのは、 2,3を因数に持たない数、つまり1,5,7,11 のみである。
一方、p2 は法 12における平方剰余数でもある。
法 12における平方剰余数は、
| a | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| a2 | 0 | 1 | 4 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 4 | 1 |
と、 0,1,4,9の四つしかない。
よって、双方の条件を満たすp2 は、
p2≡1(mod 12)しか存在しない。
【問題5】
1)n=1の場合

で成立。
2)n=k-1 で成立していると仮定する
(チーム xiはそれぞれ k-1勝k-1 敗)
ここで、 x2k,x2k+1の2チームを追加することを考える。
チームx2k は、x1 から xkまでのチームに勝利( k勝)し、
xk+1から x2k-1までのチームに敗北( k-1敗)し、
さらにチーム x2k+1に敗北( 1敗)させる。
同様に、チーム x2k+1は、 x1 から xk までのチームに敗北( k敗)し、
xk+1から x2k-1までのチームに勝利( k-1勝)し、
さらにチームx2k に勝利( 1勝)させる。
すると、x2k,x2k+1 ともに、k 勝 k敗。
x1から x2k-1までのチームは、それぞれ x2k,x2k+1のどちらかに勝ってどちらかに負けるので
k-1勝k-1 敗に 1勝1 敗ずつ加えて k勝k 敗。
よって、 n=k-1で成立している場合、 n=kでも成立しうる。
3)1)と2)から、nが正整数の場合、どのチームもn 勝n敗になり得る。
【感想】
特に問4.をやってみて思ったのですが、よくこういう問題を思いつきますね。
実際に計算してみて、「本当にそうなるんだ」という驚きがありました。
面白いものです。
同様に、P2>6を満たす素数P(>3)はP2≡1(mod6)ですし、
P2>8を満たす素数PはP2≡1(mod8)ですね。
(他にもありそうな気がします。無限にあるかどうかは、また問題になりそうですね)
◆宮城県 甘泉法師 さんからの解答。
【問題2】
題意の多面体が存在するとする。
各頂点ごとに集まる辺の数は奇数。頂点は奇数個なのでこれを足しあげると奇数。
一方、ひとつの辺は2回数えられるので足しあげると偶数。
矛盾するので題意の多面体は存在しない。
【問題4】
(P-1),(P+1)ともに偶数なので (P-1)(P+1)は4の倍数。
(P-1),(P+1)のどちらかは必ず3の倍数なので(P-1)(P+1)は3の倍数。
これから P2 - 1 は12の倍数となり P2を12で割ると必ずあまりは1。
◆愛知県 Y.M.Ojisan さんからのコメント。
【問題4コメント】
24で割っても1あまりです。
∵Pは3の倍数でなく 2の倍数でもありません。
従って P=3n±1,P=4m±1です。
よって P2-1=3(3*n2±2*n)=8(2m2±m) です。
即ちP2-1は3と8の倍数です。
◆宮城県 甘泉法師 さんからの解答。
【問題3】
題意の3数に関係 2B=A+C が成り立つと仮定する。
A,B,Cの表記には 0と1しかでなく
B=0110...1010 (3進表記) なら 2B=0220...2020 (3進表記)のように1が2に置き換わり2Bの表記に1は現れない。
ところが互いに異なるA、Cについて A+C の3進法表記には必ず1があらわれる。
例
A = 100011
+) B = 10101
-----------------
A+B= 110112 繰り上がりはない。よって上記の仮定は成り立たない。
【問題5】
例を示す。
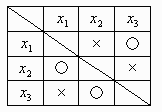
勝敗表でW(勝)とL(負)が上下左右で反対の、対角線をはさんだ市松模様にすればよい。
| α | β | γ | δ | .. | ω | |
| プレイヤーα | x | W | L | W | .. | L |
| プレイヤーβ | L | x | W | L | .. | W |
| プレイヤーγ | W | L | x | W | .. | L |
| プレイヤーδ | L | W | L | x | .. | W |
| ....... | ||||||
| プレイヤーψ | L | .. | x | W | ||
| プレイヤーω | W | .. | W | x | ||
◆出題者のコメント。
Y.M.Ojisan さん、大空風成 さん、MISERY さん、永山祐介 さん、甘泉法師 さん解答ありがとうございます。
いろんな証明方法があって面白いですね。
ちなみに、私の考えていた【問題1】と【問題5】の証明は以下でした。
【問題1】
(n+1)kー1 は、(n+1)進法で表すと、0でなければ全k桁ともnです。
明らかに、どちらであってもnで割り切れます。
【問題5】
各チームを異なる点と考え、すべての対戦を2点間を結ぶ線で表すと、どの点も2n本の線があります。
2nは偶数なので、明らかにすべての線は一筆書きできる筈です。
仮に一筆書きしたものとすると、どの点においても、n本の線は入り、n本の線は出ています。
そこで、[入る線は勝ち],[出る線は負け]とすると、明らかにどのチームもn勝n敗です。
さらに3題ほど追加しましたので、これらの問題にも挑戦してみてください。
◆大阪府 Rolec_taka さんからの解答。
【問題7】
元の弦の長さを2a,中点を通る弦の長さをb+cとおく。
すなわち、弦をAB,CDとおく。
そして、交点をPとする。
AP=BP=a CP=b DP=cとする。
方べきの定理より、a2=bc=kとおく
AB=2a=2√k
| CD=b+ | k b | ≧2√k(相加相乗平均の不等式) |
| 今、この式の等号成立はb= | k b | 、すなわちb=c。 |
◆大阪府 らぶりぃナナちゃん さんからの解答。
【問題6】
(1)Pより、Aさんは本当の事を言ったり、嘘をついたりする人とする。
(2)Qと(1)より、BさんはAさんと常に真偽が異なることを言う人とする。
(3)Rと(2)より、AさんBさんのどちらかが嘘をつくので、Cさんは常に嘘をつく。
(4)Qと(3)より、Dさんは常に本当のことを言う。
◆宮城県 甘泉法師 さんからの解答。
【問題6】
命題Pから、あるときには本当のことも言うが、別なときにはウソもつく人が存在し、これをpとする。
命題Qから、pが本当のことを言うときには常にウソをつき、ウソをつくときには常に本当のことを言う人が
存在し、これをqとする。
命題Rから、pとqが、2人とも本当のことを言うときには常に本当のことを言い、1人でもウソをつくとき
には常にウソをつく人が存在し、これをrとする。
rは常にウソをつく。
命題Qからrが本当のことを言うときには常にウソをつき、ウソをつくときには常に本当のことを言う人が必
ず存在し、これをtとする。
tは常に本当のことを言う。
よって常に本当のことを言う人が必ず存在する。
【問題7】
円の中心Oから弦に引いた垂線は弦の中点Aを通る。
点O、点Aと弦のひとつの端点のつくる三角形の三平方の定理から円の中心から弦に引いた垂線の長さが短いほ
ど弦は長い。
円の中心Oから、元の弦の中点を通る別の弦に引いた垂線は、新しい弦の中点Bを通る。
直角三角形OBAの三平方
の定理から
OBの長さ < OAの長さ
これから直径以外の弦において、その中点(だけ)を通る弦は、元の弦よりも必ず長い。
【問題8】
青線は円(半径1とする)に内接する正三角形の1辺なので
その長さの自乗は余弦定理から
12+ 12- 2*1*1*cos120度 = 3
正12角形の面積は
12*1*1*1/2*sin30度 = 3
でともに3になる。
◆出題者のコメント。
Rolec_taka さん、らぶりぃナナちゃん さん、甘泉法師 さん、追加問題の解答ありがとうございます。
いずれの証明も実にみごとだと思います。
ちなみに、私の考えていた【問題8】の証明は以下でした。
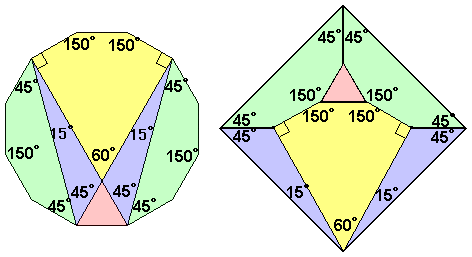
正12角形を、左の図のような4本の対角線で6つに切り離し、右の図のように寄せ合わせると、
明らかに示された対角線が1辺となる正方形です。
総じて、期待以上にいろんな証明方法が寄せられ、出題者としては嬉しい限りです。
私には思いつくことすらできなかった証明方法もいくつかあり、とても勉強になりました。
自分で証明するのは当然ですが、自分とは別な証明方法に遭遇するのも違った意味で楽しいものですね。