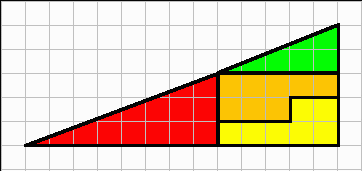
◆不思議な穴？
今回はアメリカのゲーム研究家マーチン・ガードナーによるパラドックスです。
【問題１−１】
今、下の直角三角形を図のように分割します。
これを並び替えると、下の直角三角形になります。
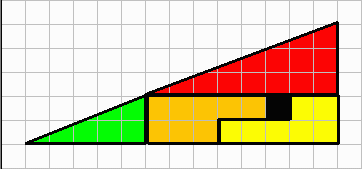
底辺や、高さは変わっていません。
あれ、よく見るとなぜか穴があいている？？？
いったいなぜ、このようなことがおこったのでしょうか。
【問題１−２】
この問題とフィボナッチ数列との関係を見つけてください。
それでは実際に実験してみましょう。
図の直角三角形を組み替えて、下の直角三角形を作ってみてください。
図形の中央付近でマウスの左ボタンをクリックし、ボタンを押しながら動かすと、図形を移動することができます。
前回の問題に続いて今回もフィボナッチ数列と深い関係があります。
そこでおまけとしてフィボナッチ数列の性質をいくつか調べてみましょう。
高校生以上の人は、できれば証明も考えてください。
Ｆ1＝Ｆ2＝１、
Ｆ3＝１＋１＝２、
Ｆ4＝１＋２＝３、
Ｆ5＝２＋３＝５、
Ｆ6＝３＋５＝８、
Ｆ7＝５＋８＝１３、
Ｆ8＝８＋１３＝２１、
Ｆ9＝１３＋２１＝３４、
Ｆ10＝２１＋３４＝５５、
・ ・ ・ ・
【おまけ１】
フィボナッチ数（フィボナッチ数列にでてくる数）Ｆnが偶数になるのは、ｎがどのような場合でしょうか。
【おまけ２】
Ｆnが５の倍数になるのは、ｎがどのような場合でしょうか。
【おまけ３】
Ｆnが４の倍数になるのは、ｎがどのような場合でしょうか。
【おまけ４】
Ｆnが７の倍数になるのは、ｎがどのような場合でしょうか。
◆参考
フィボナッチの数列の一般項は、
| ｜ |
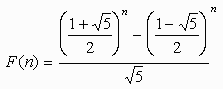
1- ―――― 2 | ｜＜１ |
なので、ｎが大きくなると、
| ( |
1- ―――― 2 | ) | n→０ |
したがって、Ｆnの概数は
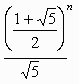で、電卓で簡単に求めることができます。
実はＦnは
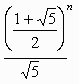に最も近い整数になります。
◆よろしければ電卓をお使いください。
解答用紙はこちらです。
| No. | 解答時刻 | 正解者 | |
| １ | 10/31 SUN 10:12 | 清川 育男 さん | 一般 |
| ２ | 10/31 SUN 13:51 | 迷える羊 さん | 一般 |
| ３ | 11/ 2 TUE 1:40 | 緑川 正雄 さん | 一般 |
| ４ | 11/ 3 WED 7:58 | ゆうきリンリン さん | 中学３年 |
| ５ | 11/ 4 THU 11:37 | ＬＯＶＥ マシーン さん | 中学３年 |
| ６ | 11/ 4 THU 17:34 | アステカイザー さん | 一般 |
| ７ | 11/ 4 THU 22:41 | くうちゃん さん | 高校生 |
| ８ | 9/13 FRI 22:42 | you さん | 一般 |
| ９ | 9/13 FRI 22:43 | チーコ さん | 一般 |
| 10 | 11/21 MON 19:01 | lovelever さん | 中学３年 |
◆過去問はこちらです。
◆ 今週の問題へ
数学の部屋へもどる。