『今週の問題』第69回　解答

◆石川県　迷える羊 さんからの解答

【問題１−１】

もとの直角三角形は下の辺の長さが１３、右の辺の長さが５であるから、赤や緑の三角形の左下の角θは、

tanθ＝

５ ―――― １３

ここで、赤の三角形の下の辺の長さをａとする。
【０＜ａ＜１３】

緑の三角形の下の辺の長さは、１３−ａ。

橙色と黄色の図形は、横の長さ１３−ａ、
縦の長さａ･tanθの長方形Ｓを、２つに分割したものである。

分割する線の横線は、長方形の縦辺を垂直に３等分する線と一致する。
縦線は、長方形の左から３／５の位置にある。

よって、並べ替えた時の橙色と黄色と黒色の合計の長方形Ｔは、

横の長さ

８ ―― ５

（１３−ａ）

縦の長さ

２ａ･tanθ ―――――― ３

である。

この長方形Ｔと緑の三角形の横の長さの合計が１３にならなければならない。

８ ―― ５

（１３−ａ）＋１３−ａ＝１３

ａ＝８

このとき、長方形Ｔの縦の長さは、

２ａ･tanθ ―――――― ３

＝

８０ ―――― ３９

緑の三角形の縦の長さは、

（１３−ａ）tanθ＝

２５ ―――― １３

赤の三角形の縦の長さは、

ａ･tanθ＝

４０ ―――― １３

よって、もとの三角形と合同な枠に並べ替えたパーツを収めようとすると、橙色と黄色の上の部分と赤の下の部分が重なり合って収まらない。
この重なり合う部分の面積が黒い部分の面積と等しくなる。

【問題１−２】

もとの直角三角形の各頂点を、Ａ,Ｂ,Ｃとする。

ＡＢ＝Ｆ(n),ＢＣ＝Ｆ(n-2),ＡＢ⊥ＢＣ

直線ＢＣと平行で辺ＡＢを、
Ｆ(n-1)：Ｆ(n-2)に内分する点Ｄを通る直線と辺ＡＣとの交点をＦとする。

点Ｆを通り、直線ＡＢと平行な直線と辺ＢＣとの交点をＥとする。

線分ＦＤを３等分する点にＦＤと垂直な線を引き、下の線とＦＤとの交点を点Ｇ、上の線とＥＢとの交点をＨとする。

線分ＦＤに平行で、線分ＤＢをＦ(n-3)：Ｆ(n-4)に内分する点を通り、ＤＢに垂直な直線と、先ほどの３等分線との交点を、上から順に、点Ｉ,点Ｊとする。

図形ＦＧＪＩＨＥと図形ＧＤＢＨＩＪとを、上の図形の辺ＩＪと下の図形の辺ＧＤを重ねる様に置くと、
縦の長さ２Ｆ(n-1)Ｆ(n-2)／３Ｆ(n)、
横の長さＦ(n-2)＋Ｆ(n-3)の長方形から、
その上辺に接する縦の長さＦ(n-1)Ｆ(n-2)／３Ｆ(n)、
横の長さＦ(n-3)−Ｆ(n-4)の長方形をくり貫いた図形になる。

この図形をＸとして、その上辺に辺ＡＤを重ね、右上の頂点に点Ａを重ねて、△ＡＤＦを置く。

またＸの左辺に辺ＣＥを重ね、点Ａと同じ位置に点Ｃを重ねて、△ＣＦＥを置く。

これで図形の変換は終了する訳であるが、

△ＡＤＦ∽△ＣＦＥ,ＡＤとＦＥは平行だから、斜辺は一致している。

図形Ｘの全体の縦の長さχは、
χ＝２Ｆ(n-1)Ｆ(n-2)／３Ｆ(n)

△ＣＦＥの辺ＣＥの長さは、Ｆ(n-2)²／Ｆ(n)

今、Ｆ(n)＝Ｆ(n-1)＋Ｆ(n-2)だから、

χ−ＣＥ
＝｛２Ｆ(n-1)−３Ｆ(n-2)｝Ｆ(n-2)／３Ｆ(n)
＝Ｆ(n-5)Ｆ(n-2)／３Ｆ(n)

今、Ｆ(n)＞０だから、χ＞ＣＥ

よって、図形Ｘは△ＣＦＥの下辺より少し下にはみ出している。

なお、同様にすると、図形Ｘの右辺は△ＡＤＦの右辺と完全に繋がっている。

図形Ｘの下にはみ出している部分は、
横の長さＦ(n-2)＋Ｆ(n-3)、
縦の長さ（χ−ＣＥ）の長方形である。

その面積は、

｛Ｆ(n-2)＋Ｆ(n-3)｝×｛Ｆ(n-5)Ｆ(n-2)／３Ｆ(n)｝
＝Ｆ(n-1)Ｆ(n-2)Ｆ(n-5)／３Ｆ(n)

図形Ｘで、くり貫かれている長方形の面積は、

｛Ｆ(n-1)Ｆ(n-2)／３Ｆ(n)｝×｛Ｆ(n-3)−Ｆ(n-4)｝
＝Ｆ(n-1)Ｆ(n-2)Ｆ(n-5)／３Ｆ(n)

よって、面積は等しい。

【おまけ１】

『Ｆ(n)が偶数』と『ｎが３の倍数』とが同値である事を証明する。

≪ア≫
まず、Ｆ(1)＝Ｆ(2)＝１であるから、
ｎ＝1,2のとき、Ｆ(n)は奇数。

Ｆ(3)＝Ｆ(1)＋Ｆ(2)であるから、
ｎ＝3のとき、Ｆ(n)は偶数。

≪イ≫
ｎ＝３ｋのとき、Ｆ(n)は偶数で、
Ｆ(n-1),Ｆ(n-2)が奇数だと仮定する。
【ｋは自然数】

Ｆ(3(k+1)-2)＝Ｆ(3k)＋Ｆ(3k-1)
Ｆ(3(k+1)-1)＝２Ｆ(3k)＋Ｆ(3k-1)
Ｆ(3(k+1))＝３Ｆ(3k)＋２Ｆ(3k-1)

今、Ｆ(3k)は偶数で、Ｆ(3k-1)は奇数だから、
ｎ＝３（ｋ＋１）のときも、成立する。

≪ア≫,≪イ≫より、ｎが３の倍数。

【おまけ２】

ｎが５の倍数。

【おまけ３】

ｎが６の倍数。

【おまけ４】

ｎが８の倍数。
≪以上、証明は【おまけ１】と同様。≫

◆千葉県　緑川　正雄 さんからの解答

【問題１−１の回答】

水平方向をx軸とし右方向を正、垂直方向をy軸とし上方向を正に座標軸を取る。

上の図形の斜面の方程式を求めると、
図のx=0〜 8までの斜面の傾きは3/8であり、

斜面はy=

3 ― 8

x で表される。

x=8〜13までの斜面の傾きは2/5であり、

斜面はy=

2 ― 5

(x-8)+3 で表される。

よって、斜面と図形の右端の直線、下の直線で囲まれる面積は、

8 ∫ 　0

3 ― 8

dx+

13 ∫ 　8

{

2 ― 5

(x-8)+3}dx=32

下の図形の斜面の方程式を求めると、
図のx=0〜 5までの斜面の傾きは2/5であり、

斜面はy=

2 ― 5

x で表される。

x=5〜13までの斜面の傾きは3/8であり、

斜面はy=

3 ― 8

(x-5)+2 で表される。

よって、斜面と図形の右端の直線、下の直線で囲まれる面積は、

5 ∫ 　0

2 ― 5

x dx+

13 ∫ 　5

{

3 ― 8

(x-5)+2}dx=33

であり、下の図形の斜面と図形の右端の直線、下の直線で囲まれる面積は上の図形の斜面と図形の右端の直線、下の直線で囲まれる面積より1大きい。

よって、上の図の分割した各部分を下の図のように並び替えると面積1だけ不足が生ずる。

【問題１−２の回答】

上の図形の面積Sは、

S=1/2×{F(3)×F(5)+F(4)×F(6)}+F(4)×F(5)

下の図形の穴の空いている部分も含めた面積Tは、

T=1/2×{F(3)×F(5)+F(4)×F(6)}+F(3)×F(6)

で表される。

よって、

S-T
=F(4)×F(5)-F(3)×F(6)
=F(4)×F(5)-F(3)×{F(4)+F(5)} =F(4)×{F(5)-F(3)}-F(3)×F(5)
=F(4)×F(4)-F(3)×F(5)
=(-1)⁵　[第68回　問題3]
=-1

となり、下の図形の穴の空いている部分も含めた面積の方が大きい。

【おまけ】

F(1)=1　…(1)
F(2)=1　…(2)
F(n+2)=F(n)+F(n+1)　[n≧1] …(3)より、

F(n+3)
=F(n+1)+F(n+2)
=F(n)+2×F(n+1) …(4)

よって、
F(n+3)≡F(n) [mod2]…(4)’

(3)、(4)より
F(n+4)
=F(n+2)+F(n+3)
=2×F(n)+3×F(n+1) …(5)

よって、
F(n+4)≡2×F(n) [mod3]…(5)’

(4)、(5)より
F(n+5)
=F(n+3)+F(n+4)
=3×F(n)+5×F(n+1) …(6)

よって、
F(n+5)≡3×F(n) [mod5]…(6)’

(5)、(6)より
F(n+6)
=F(n+4)+F(n+5)
=5×F(n)+8×F(n+1)…(7)

よって、
F(n+6)≡5×F(n) [mod8]…(7)’

(6)、(7)より
F(n+7)
=F(n+5)+F(n+6)
=8×F(n)+13×F(n+1)…(8)

よって、
F(n+7)≡8×F(n) [mod13]…(8)’

(7)、(8)より
F(n+8)
=F(n+6)+F(n+7)
=13×F(n)+21×F(n+1) …(9)

よって、
F(n+8)≡13×F(n) [mod21]…(9)’

【おまけ1の回答】

F(3n)[n≧1]だけが偶数である。

【理由】

(4)、(4)’の関係式を順次適用すると、n≧1の時

F(3n+1)
≡F(1) [mod2]
≡1 [mod2]
0 [mod2]

F(3n+2)
≡F(2) [mod2]
≡1 [mod2]
0 [mod2]

F(3n+3)
≡F(3) [mod2]
≡2 [mod2]
≡0 [mod2]

F(3)とF(3n+3)[n≧1]のみが2で割り切れる。
即ち F(3n)[n≧1]だけが偶数である。

【おまけ2の回答】

F(5n)[n≧1]だけが5の倍数である。

【理由】

(6)、(6)’の関係式を順次適用すると、n≧1の時

F(5n+1)
≡(3ⁿ)×F(1) [mod5]
≡(3ⁿ)×1 [mod5]
≡3ⁿ [mod5]
0 [mod5]

F(5n+2)
≡(3ⁿ)×F(2) [mod5]
≡(3ⁿ)×1 [mod5]
≡3ⁿ [mod5]
0 [mod5]

F(5n+3)
≡(3ⁿ)×F(3) [mod5]
≡(3ⁿ)×2 [mod5]
0 [mod5]

F(5n+4)
≡(3ⁿ)×F(4) [mod5]
≡3ⁿ⁺¹ [mod5]
0 [mod5]

F(5n+5)
≡(3ⁿ)×F(5) [mod5]
≡(3ⁿ)×5 [mod5]
≡0 [mod5]

F(5)とF(5n+5)[n≧1]のみが5で割り切れる。
即ち F(5n)[n≧1]だけが5の倍数である。

【おまけ3の回答】

F(6n)[n≧1]だけが4の倍数である。

【理由】

(7)、(7)’の関係式を順次適用すると、n≧1の時

F(6n+1)
≡(5ⁿ)×F(1) [mod8]
≡(5ⁿ)×1 [mod8]
≡5ⁿ [mod8]
0 [mod8]

F(6n+2)
≡(5ⁿ)×F(2) [mod8]
≡(5ⁿ)×1 [mod8]
≡5ⁿ [mod8]
0 [mod8]

F(6n+3)
≡(5ⁿ)×F(3) [mod8]
≡(5ⁿ)×2 [mod8]
0 [mod8]

F(6n+4)
≡(5ⁿ)×F(4) [mod8]
≡(5ⁿ)×3 [mod8]
0 [mod8]

F(6n+5)
≡(5ⁿ)×F(5) [mod8]
≡5ⁿ⁺¹ [mod8]
0 [mod8]

F(6n+6)
≡(5ⁿ)×F(6) [mod8]
≡(5ⁿ)×8 [mod8]
≡0 [mod8]

F(6)とF(6n+6)[n≧1]のみが8で割り切れる。
即ち F(6n)[n≧1]だけが4の倍数である。

【おまけ4の回答】

F(8n)[n≧1]だけが7の倍数である。

【理由】

(9)、(9)’の関係式によれば、n≧1の時

F(8n+1)
≡(13ⁿ)×F(1) [mod21]
≡(13ⁿ)×1 [mod21]
≡13ⁿ [mod21]
0 [mod21]

F(8n+2)
≡(13ⁿ)×F(2) [mod21]
≡(13ⁿ)×1 [mod21]
≡13ⁿ [mod21]
0 [mod21]

F(8n+3)
≡(13ⁿ)×F(3) [mod21]
≡(13ⁿ)×2 [mod21]
0 [mod21]

F(8n+4)
≡(13ⁿ)×F(4) [mod21]
≡(13ⁿ)×3 [mod21]
0 [mod21]

F(8n+5)
≡(13ⁿ)×F(5) [mod21]
≡(13ⁿ)×5 [mod21]
0 [mod21]

F(8n+6)
≡(13ⁿ)×F(6) [mod21]
≡(13ⁿ)×8 [mod21]
0 [mod21]

F(8n+7)
≡(13ⁿ)×F(7) [mod21]
≡13ⁿ⁺¹ [mod21]
0 [mod21]

F(8n+8)
≡(13ⁿ)×F(8) [mod21]
≡(13ⁿ)×21 [mod21]
≡0 [mod21]

F(8)とF(8n+8)[n≧1]のみが21で割り切れる。
即ち F(8n)[n≧1]だけが7の倍数である。

【◆参考】

F(1)=1 …(1)
F(2)=1 …(2)
F(n+1)=F(n)+F(n-1) [n≧2] …(3)

(3)を

F(n+1)-α×F(n)=β×{F(n)-α×F(n-1)} …(4)

で表すと、

α+β=1,α×β=-1 …(5)

であるからα,βは

t²-t-1=0の根

1+ ―――― 2

，

1- ――――― 2

である。

上の根は実数であり、β＞αと仮定して、一意性は失われない。

α＝

1- ―――― 2

β＝	1+ ――――― 2

と置く。

F(n+1)-α×F(n)
=β×{F(n)-α×F(n-1)}
={β^n-1}×{F(2)-α×F(1)}
={β^n-1}×(1-α) [(1),(2)より]
=βⁿ [(5)より] …(6)

式(4)を変形すると

F(n+1)-β×F(n)=α×{F(n)-β×F(n-1)} …(7)

であるから、式(6)を求めた方法と同様の方法に基づき

F(n+1)-β×F(n)=αⁿ …(8)

となり、 (6)-(8)より

(β-α)×F(n)={βⁿ-αⁿ} …(9)

を得る。

ところで,β-α=であるから、

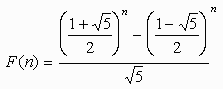…(10)

F(n)は条件：n≧2で求められたが、式(10)はF(1)=1を満足するので、
n≧1に対して成立する。

　◆　問題へもどる

　◆　今週の問題へ

数学の部屋へもどる