『元に戻る交換』

【問題】

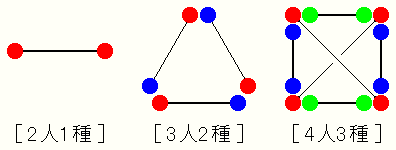
ｎ(≧２)人のそれぞれがすべて異なる(ｎー１)個の玉を等しく持っています。
そこで、それぞれは初めに持っていた玉すべてを他の全員とお互いに１個ずつ交換します。

ところが、この交換は次の２通りしか許されません。

（１）すべての交換において、どの交換も異種同士にさせる。
（２）すべての交換において、どの交換も同種同士にさせる。

さて、ここで問題です。

全員とも初めの状態に戻る交換の方法が、ｎに関係なく必ずあるでしょうか？
ある場合もない場合も、その理由を示してください。。

【追加問題】

Y.M.Ojisan さんの解答より、以下の２つの事実が示されました。

それでは、次の条件を満たすそれぞれのｎはあるでしょうか？

（１）同種同士の交換だけで、ｎ人全員が元の状態に戻る奇数ｎ
（２）異種同士の交換だけで、ｎ人全員が元の状態に戻る偶数ｎ

ある場合もない場合も、その理由を示してください。