『最大値と最小値』

【問題１】

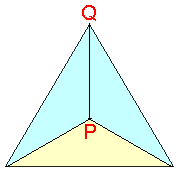
図は正四面体を真上から見たものである。

現在、正四面体の底面の中心に点ｓがあり、頂点Ｐに点ｔがある。
点ｓは図の薄黄色の面の中心に向い、点ｔは頂点Ｑに向かい、同時に出発する。
どちらも正四面体の表面の最短コースを移動するが、速さは点ｔが点ｓの倍である。

正四面体の１辺の長さを１としたとき、ｓ-ｔ間の距離の最大値と最小値を求めよ。

【問題２】

仲間同士の(ｎ＋１)人が全員座ろうとすると、あいにく席はｎ人分しかなかった。
（ただし、ｎは自然数とする。）

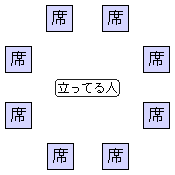
やむを得ず１人だけが立ったままとなったが、以下のルールを決めた。

立っている人は、自分が席を譲ったことも譲られたこともない人に限り、誰にでも[席譲り]を要求できる。 要求された人は、条件を満たしている要求ならば、すぐ席を譲ってやらなければならない。

このルールだと、[席譲り]を延々と繰り返すと必ず行き詰まり、もはや席は譲ってもらえなくなる。
行き詰まるまでの[席譲り]総回数の、最大値と最小値をｎで表せ。

　解答用紙はこちらです。　【寄せられた解答】

　数学の部屋へもどる