『不可能である証明』

【問題１】

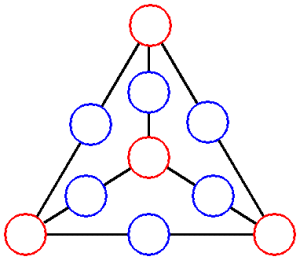
図は正四面体を真上から見たものです。
４つの頂点上と６つの辺上に、それぞれ１つずつ任意の連続した整数１０個を置くものとします。

【問題１－１】

辺上の整数を両サイドの頂点上の整数の和とさせるのは不可能であることを示してください。

【問題１－２】

辺上の整数を両サイドの頂点上の整数の差の絶対値とさせるのは不可能であることを示してください。

【問題２】

図は１×２のサイズのタイルを、５×６の長方形に張り詰めた２つの例です。

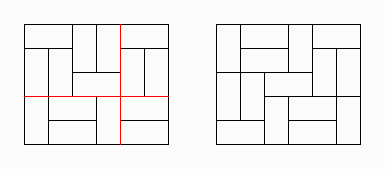
左の張り詰め方には、赤線で示したような分断線(長方形を２分する線分)が２本あります。
ところが、右の張り詰め方には、そのような分断線は１本もありません。

６×６の正方形では、同じタイルを分断線がないように張り詰めるのは不可能であることを示してください。