◆大阪府 ゆたか さんからの解答。
【問題1】(準備)
10個の連続する整数を
n,n+1,n+2,・・・,n+9
とすると、これらの和は
(1/2)×10×(n+n+9)=5(2n+9)
となり、これは奇数である。
【問題1−1】(証明)
4つの頂点に置く整数をA,B,C,Dとすると、6つの辺に置く整数はそれぞれ
A+B,A+C,A+D,B+C,B+D,C+D
となるので、10個の整数の和は、
4A+4B+4C+4Dである。
これは偶数であるから、前述の内容に合わない。
したがって、題意のような配置は不可能である。
【問題1−2】(証明)
1−1のように頂点の整数を定め、
さらに、A>B>C>Dとすると、6つの辺に置く整数はそれぞれ
A−B,A−C,A−D,B−C,B−D,C−D
となり、10個の整数の和は、4A+2B−2Cとなる。
これも偶数であるから、1−1と同様に題意のような配置は不可能である。
◆東京都 哲(サトシ) さんからの解答。
【問題1】 連続した整数10個のうち、偶数・奇数とも5個ずつである。
また、偶数同士・奇数同士の和・差は偶数、偶数と奇数の和・差は奇数である。
(i) 4つの頂点の整数のうち、1つも偶数でない場合、
10個の整数のうちの ((偶数の個数), (奇数の個数)) = (6, 4) 。
(ii) 1つだけ偶数... (4, 6) 。
(iii) 2つが偶数... (4, 6) 。
(iv) 3つが偶数... (6, 4) 。
(v) 4つとも偶数... (10, 0) 。
したがって、稜上の整数が両サイドの頂点上の整数の和(or差)であるならば、正四面体に配置された整数10個は連続し
たものでない。
正四面体に配置された整数10個が連続したものならば、稜上の整数は両サイドの頂点上の整数の和(or差)でない。
【問題1−2】

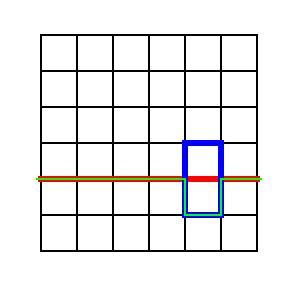
分断線が存在しないということは、赤線が青枠のような長方形を横切るということ。
ところが、青枠のような長方形は2個以上、偶数個必要です。
奇数個だと、緑線は長方形を横切らないはずですが、分けられた部分双方には奇数個の小正方形があることになります
ね。
長方形が小正方形2個から出来ているのですから、双方とも偶数個でなければなりません。
ということで、10個の分断線候補それぞれに最低でも2つずつの青枠的長方形が必要なわけです。
これらの長方形は重複することがありませんから、大正方形の中には長方形が最低でも20個なければなりません。
ところが、実際には大正方形の中には長方形は18個しかありませんね。
そういうわけで、分断線が存在しないようにすることはできないわけです。
◆出題者のコメント
早々に、解答ありがとうございます。
お二人とも鮮やかな証明だと思います。
示されたように、どちらの問題も偶奇の矛盾を利用すれば可能です。
馴染み深い「一筆書き不可能の証明」も同様に偶奇の矛盾を利用しますが、どうして不可能である証明には偶奇にからんだものが多いんでしょうかね?
そうそう、小学3年生の知人の息子さんいわく、「哲(サトシ)さんの証明は、どちらも僕にも理解できたよ。」
言われて気付いたのですが、代数が皆無。
まさに万人(億人かも)に向けた証明ですね。
ちなみに、【問題1】は私の考案ですが、【問題2】は11年前のIMO通信教育の問題です。