『整数解方程式の接近』

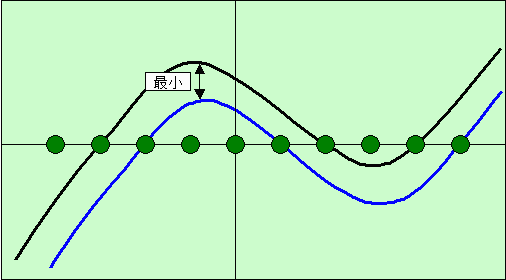
【問題１】

下記(1)の解をα₁，α₂ (2)の解をβ₁，β₂とする。
これら４個が全て異なる整数であるＡ，Ｂの組み合わせ中で　
｜Ｂ｜の最小値を求めよ。

(1) ｆ(X)＝X²＋A＝０
(2) ｆ(X)＝Ｂ

【問題２】

下記(1)の解をα₁，α₂，α₃ (2)の解をβ₁，β₂，β₃とする。
これら６個が全て異なる整数であるＡ₀，Ａ₁， Ｂの組み合わせ中で　
｜Ｂ｜の最小値を求めよ。

(1) ｆ(X)＝X³＋A₁X＋A₀＝０
(2) ｆ(X)＝Ｂ

【問題３】

下記(1)の解をα₁〜α₄， (2)の解をβ₁〜β₄とする。
これら８個が全て異なる整数であるＡ₀，Ａ₁，Ａ₂，Ｂの組み合わせ中で
｜Ｂ｜の最小値を求めよ。

(1) ｆ(X)＝X⁴＋A₂X²＋A₁X＋A₀＝０
(2) ｆ(X)＝Ｂ

【おまけ】

下記(1)の解をα₁〜α_n ，(2)の解をβ₁〜β_n とする。
これら２ｎ個が全て異なる整数であるＡ_i，Ｂの組み合わせ中で
｜Ｂ｜の最小値ないし下限をｎの関数として求めよ。

(1) ｆ(X)＝Xⁿ＋A_n-2X^n-2＋〜＋A₂X²＋A₁X＋A₀＝０
(2) ｆ(X)＝Ｂ

注記）出題者はおまけの完全解答持たず。１以上というのは無し。

　解答用紙はこちらです。　【寄せられた解答】

　◆方程式へもどる

　数学の部屋へもどる