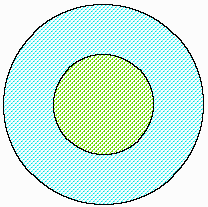
大きい円内(青と緑を合わせた部分)に刺さる確率は、小さい円内(緑の部分)に刺さる確率の何倍でしょうか。
図1のように、半径が1:2となる同心円が2個、書いてあります。
この円盤に向かって目を閉じて、針を突き刺します。
◆図1

大きい円内(青と緑を合わせた部分)に刺さる確率は、小さい円内(緑の部分)に刺さる確率の何倍でしょうか。
Aさんの答え:大きい円の面積は小さい円の4倍だから、確率は4倍です。
Bさんの答え:
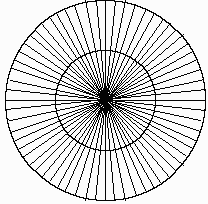
中心から図2の様に、放射線状に線分を引きます。
この線分を無数に引けば、円盤を覆い尽くすことができます。
大きい円に入る線分の長さは小さい円の2倍だから、確率は2倍です。
◆図2
さて、どちらの答えが正しいでしょうか。
それとも両方とも間違いで、別の答えがあるのでしょうか。
◆確率問題へもどる
 数学の部屋へもどる
数学の部屋へもどる