奇数の時は3倍して1を加える。
新たにできた数について同じことを繰り返すと最後には1なる。
3倍して1を足すと偶数になるのを考慮して関数表現をすれば
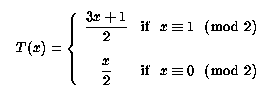
となる。
任意の自然数χがあり、χが偶数の時は2で割り、
奇数の時は3倍して1を加える。
新たにできた数について同じことを繰り返すと最後には1なる。
3倍して1を足すと偶数になるのを考慮して関数表現をすれば
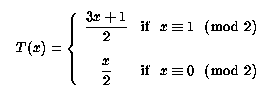
となる。
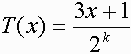
(kはT(χ)が奇数になる様に選ぶ)
これはコラッツ関数から生成される数列から偶数を除いた数列を作り出す。
この関数を繰り返すことで、任意の奇数が最終的には 1→1のループに至ることが示されればコラッツ問題の証明となります。
証明の手順
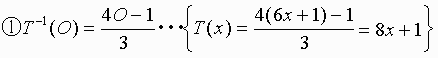
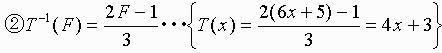
③ T-1(t)=4t+1 ・・・ T-1(t)=1 (mod6)
ここで、8χ+1、8χ+3、8χ+7が生成され、
8χ+5が生成されないように見えますが
これは①②で生成される数および3の奇倍数 a0 を初項として
a1=4a0+1、a2=4a1+1、・・・、an=4an-1+1
とする数列のa1~anに含まれる。・・・・・④
これらはコラッツの関数を適用すると
T(a0)=T(a1)=・・・T(an)となる。・・・⑤
この数列に含まれる数の集合を集合a0などと呼ぶこととする。
以上ですべての奇数についての写像が完成しました。
また、数列⑤のすべての和集合はすべての奇数の集合でありかつ重複がない。
最初の方を表にまとめると
| χ | T-1(χ) | |||||
|---|---|---|---|---|---|---|
| T(χ) | χ | |||||
| 1 | 1 | 5 | 21 | 85 | 341 | 1365 |
| 5 | 3 | 13 | 53 | 213 | 853 | 3413 |
| 7 | 9 | 37 | 146 | 597 | 2389 | 9557 |
| 11 | 7 | 29 | 117 | 469 | 1877 | 7509 |
| 13 | 17 | 69 | 277 | 1109 | 4437 | 17749 |
| 17 | 11 | 45 | 181 | 725 | 2901 | 11605 |
| 19 | 25 | 101 | 405 | 1621 | 6485 | 25941 |
| 23 | 15 | 61 | 245 | 981 | 3925 | 15701 |
| 25 | 33 | 133 | 533 | 2133 | 8533 | 34133 |
| 29 | 19 | 77 | 309 | 1237 | 4949 | 19797 |
| 31 | 41 | 165 | 661 | 2645 | 10581 | 42325 |
| 35 | 23 | 93 | 373 | 1493 | 5973 | 23893 |
| 37 | 49 | 197 | 789 | 3157 | 12629 | 50517 |
| 41 | 27 | 109 | 437 | 1749 | 6997 | 27989 |
逆関数を使い、小さい数字から調査します。
1の場合1を初項とする数列(集合1)に射影される。
1→1の場合ループであるが、その他の場合は自分自身より大きくなる。
また、ループを構成する数を初項とする集合からは再びループが生じることはないので、集合1の各元から生成される数はループになることはない。
3の場合、3より大きくなる。
5の場合の写像は集合3になり、自分自信より小さくなるのは3のみ。
3の倍数は 4χ+1なので5より大きくなる。
7の場合すべて自分自身より大きくなる。
11の場合、自分より小さくなるのは7のみ。
7は自分自身より大きくなることがわかっているので11より小さな数になるのは9または11。
9は3の奇数倍。11は自分自身。よって11はループになるか自信より大きくなる。
任意の奇数Nの場合は、Nより小さくなるか、大きくなるかのどちらかである。
Nより小さな数になった場合はNと同じになるかより大きな数になる。
以上より、すべての奇数NはループになるかNより大きな数になる。
これをコラッツ関数にあてはめると
任意の奇数はループになるか自信より小さな数になるので、1-1のループ以外にループがなければ最後には1-1のループに至る。
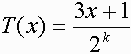
(kはT(χ)が奇数になる様に選ぶ)
2、逆関数。
あらためて定義し直します。
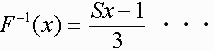
ここで S は 2 または 4 で、O=4、F=2 と記号表記する。
さらに、数列を生み出すため 4χ+1 を行うので、このために T=4 を使用する。
また、Fの右肩の数字はχに対してこの関数をN回適用する事を意味する。
3、逆関数をN回行った場合(1回目に S=4、χ≡1(mod6)から開始した場合)
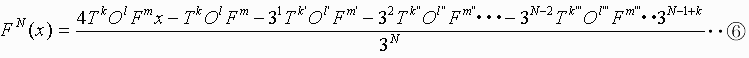
ここで、l+m=N-1+k、l’+m'+1=N-1+k、・・・・
分子の各項中の指数の和が N-1+k となる。
また k≧k'≧k''≧k'''、・・・、
l≧l'≧l''≧l'''、・・・、
m≧m'≧m''≧m'''、・・・となる。
+符号の項は4χ+1 を行った時のもので、Tの指数が一つ前の項より1減り3の指数が1増える。
その他の指数は同じ。
⑥式を書き直すが、Tの項(4χ+1を行った項)があると複雑なのでとりあえずはずして考える。
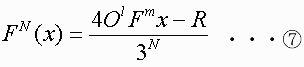
ここで l+m=N-1、Rは分子の定数項の和
⑦式=χ でループとなるのでχについて整理すると
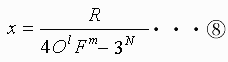
このχに1以外の整数解が無ければよい。
4-②、ループするχの範囲
⑧式のNとχの関係には、Nに対してのχの最大値が決まります。
χmax(l、m、N) < J(N) ・・・・・・・⑨(仮定1)
なる J(N)がある。
またこのJ(N)は
J(N) < 2・3N-1 ・・・・・・・・・・・・・⑩(仮定2)
なる関係がある。
0<χ<2・3N-1 なるχにはループになる条件が無い。(仮定3)
(仮定1)(仮定2)
⑧式の分母より4(=O)の指数 l に最大値があり、RはN-1個の2,3,4からなる積のN個の項で成り立っているので
Nによって決まる最大値 J(N) がある。
また、それは 2・3N-1 よりも小さいことを N=550 までコンピュータにより調査し確かめた。
(定数項の和 R の一般項は複雑なので)
その範囲は
log(χ)/((N-1)log(3)+log(2)) < 0.8
となり、Nの大きなところでは この値はほぼ0.16内外であり、Nの増大によって更に小さくなる。
χ<0では、⑧式の分母より4(=O)の指数 l に最大値が無い(4χ+1を何回でも行える)。
ただし、⑧式の m=0 の場合はχ=1となり、1→1、または5→1→1などのループが得られる。
Tの項(4χ+1を行った項)をはずしていたが、この項は⑧式のχを小さくするので、
χmax(l、m、N)< J(N)の範囲に影響はない。
(仮定3)
逆関数によって生成される数列
FN(χ)、{N=0,1,2,・・・・}はχにより一意に定まる。
この数列は非常にランダムであるが、mod6 で表した場合規則性が現れる。
χ=35までの数列(χ=169までの表)
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 3 | 3 | 5 | 5 | 1 | 3 | 1 | 5 | 1 |
| 5 | 5 | 3 | 5 | 5 | 1 | 3 | 1 | 5 |
| 7 | 1 | 3 | 1 | 5 | 1 | 3 | 5 | 5 |
| 9 | 3 | 1 | 5 | 1 | 3 | 5 | 5 | 3 |
| 11 | 5 | 1 | 3 | 1 | 5 | 1 | 3 | 5 |
| 13 | 1 | 5 | 5 | 1 | 3 | 1 | 5 | 1 |
| 15 | 3 | 3 | 1 | 1 | 1 | 5 | 5 | 5 |
| 17 | 5 | 5 | 1 | 3 | 1 | 5 | 1 | 3 |
| 19 | 1 | 1 | 3 | 3 | 3 | 1 | 1 | 3 |
| 21 | 3 | 5 | 3 | 5 | 3 | 3 | 5 | 3 |
| 23 | 5 | 3 | 3 | 1 | 1 | 1 | 5 | 5 |
| 25 | 1 | 3 | 3 | 3 | 1 | 1 | 3 | 3 |
| 27 | 3 | 1 | 1 | 5 | 3 | 1 | 5 | 1 |
| 29 | 5 | 1 | 1 | 3 | 3 | 3 | 1 | 1 |
| 31 | 1 | 5 | 3 | 1 | 1 | 5 | 3 | 1 |
| 33 | 3 | 3 | 3 | 1 | 1 | 3 | 3 | 5 |
| 35 | 5 | 5 | 3 | 3 | 1 | 1 | 1 | 5 |