【問題1】
上面が円形をした高さが一定のケーキがあります。
そこで、このケーキの上面の任意の3点にハエがとまったものと仮定します。
このとき、このケーキを上面の円の1直径で垂直にカットして、
片方のケーキには何処にもハエがとまらなかったようにできる確率はいくらでしょうか?
つまり、ケーキの上面の半円が無事である確率です。
ただし、ケーキの上面のどの点も等確率でハエがとまるものとします。
【問題2】
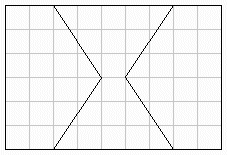
図は、与えられたケーキを上から見たものです。

ケーキの高さは一定ですが、上面は図のように
横の長さ:縦の長さ=3:2 の長方形をしています。
このケーキを3人で平等に分けたいのですが、ちょっと厄介な問題があります。
それは、ケーキの上面や垂直である全側面には一様にチョコが塗られているからです。
そのため、体積だけでなく、チョコの塗られている表面積も平等に3分割しなければなりません。
図には、ケーキを4本の線分で垂直にカットして、平等に3分割する例も示しておきましたが、 3本の線分で垂直にカットして、平等に3分割する方法はあるでしょうか?
あれば、その1例を示してください。
なければ、そのことを証明してください。
【追加問題】
【問題1ーA】
【問題1】の「任意の3点」を「任意のn点」に変えたら、半円が無事である確率はいくらになるでしょうか?
nの一般式で表してください。
ただし、ハエは点、nは自然数とします。
【問題1ーB】
無重力状態の宇宙船内の空間に、球状のケーキが浮いています。
そこで、このケーキの表面の任意のn点にハエがとまったものと仮定します。
(問題上の設定ですから、「どうして、宇宙船内にハエがいるんだ」というつっこみはナシにしてください。)
このとき、このケーキを球の中心を通る平面でカットして、片方のケーキには何処にもハエがとまらなかったようにできる確率はいくらでしょうか?
nの一般式で表してください。
つまり、ケーキの半球の表面が無事である確率です。
ただし、ハエは点、nは自然数とし、ケーキの表面のどの点も等確率でハエがとまるものとします。
◆確率問題へもどる
 数学の部屋へもどる
数学の部屋へもどる