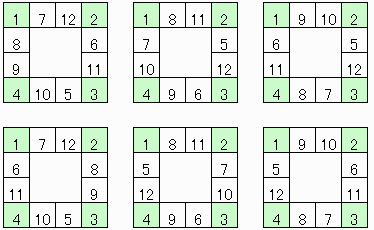
◆東京都 哲(サトシ) さんからの解答
【問題1・2】
1-2の辺,{1-4および2-3の辺(2つ)(可換)} の順で(4-3の辺には余りもの)、
(7,12),{(6,11),(8,9)}
(8,11),{(5,12),(7,10)}
(9,10),{(5,12),(6,11)}
の6通り。
【問題3】
四隅が連続4整数の条件の下では、四隅が
(1,2,3,4)および(9,10,11,12)
のときのみ解が存在します。
((9,10,11,12)の解は[問題2]の四角中の数字を13から引いてやればよいだけ。)
【おまけ】
95-96-(97-98-99*100)*101
99*(100*101-102+103)-104+105
の2通りの解が存在します。
# 逆ポーランド記法のプログラムを書くと、問中「括弧の使用...」の意味がわかります。
◆広島県 清川 育男 さんからの解答
【問題1・2】 1) 1 7 12 2
8 6
9 11
4 5 10 3
2) 1 7 12 2
6 8
11 9
4 5 10 3
3) 1 8 11 2
7 5
10 12
4 6 9 3
4) 1 8 11 2
5 7
12 10
4 6 9 3
5) 1 9 10 2
6 5
11 12
4 7 8 3
6) 1 9 10 2
5 6
12 11
4 7 8 3 以上、6通り。
【問題3】
一辺が、4N+18
1) N N+6 N+11 N+1 N+7 N+5 N+8 N+10 N+3 N+4 N+9 N+2 2) N N+6 N+11 N+1 N+5 N+7 N+10 N+8 N+3 N+4 N+9 N+2 3) N N+7 N+10 N+1 N+6 N+4 N+9 N+11 N+3 N+5 N+8 N+2 4) N N+7 N+10 N+1 N+4 N+6 N+11 N+9 N+3 N+5 N+8 N+2 5) N N+8 N+9 N+1 N+5 N+4 N+10 N+11 N+3 N+6 N+7 N+2 6) N N+8 N+9 N+1 N+4 N+5 N+11 N+10 N+3 N+6 N+7 N+2以上、6通り。
◆愛知県 Y.M.Ojisan さんからの解答
【問題1〜2】
全部で6とおり。

∵各辺合計は22である。
左右両辺はいずれも残り17を埋める必要がある。
その組み合わせは
(5,12)(6,11)(7,10)、(8,9)の4種である。
同様に上辺は(7,12)(8,11)(9,10)の3種である。
上辺を決めると、左右辺代入の組み合わせの可能性は必ず2個しか残らず、その入れ替えを除き状態が決定する。
よって3×2=6
【問題3】
可能である。
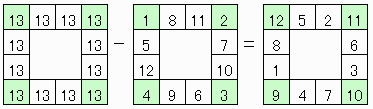
∵すくなくとも上図のように13の補数で作成したものは可能。
【おまけ】
(1) 95-96+(-97+98+99*100)*101
(2) -97+98+99*(100*101-102+103)
(3) (-97+98+99)*100*(101+102-103)
(4) 99*(100*101-102+103)-104+105
◆東京都 明 さんからの解答
【問題1】
答えの表記を簡単にするために、下記A〜Dの各々2数を表すこととします。
(問題2以下も同じ)1 A 2
B C
4 D 3
回答
A:9,10 B:5,12 C:6,11 D:7,8
【問題2】
a,b,c,dを各々A,B,C,Dの2数の和とすると
a+2=b=c=d-2
よって、
4b=4c=a+b+c+d=68
b=c=17 a=15 d=19
2数の和が17となるペアは下記4通り。
5,12 6,11 7,11 8,9
B,Cの(17となる)組み合わせは上記ペアから2つを選択する6通り。
各選択について、選択されたペア以外の2つのペアで15と17が作れるものが答えとなる。
3通りが条件に合致し、B,Cを入れ替えた下記6通りがすべて。
A:9,10 B:5,12 C:6,11 D:7,8 A:9,10 B:6,11 C:5,12 D:7,8 A:7,12 B:6,11 C:8,9 D:5,10 A:7,12 B:8,9 C:6,11 D:5,10 A:8,11 B:5,12 C:7,10 D:6,9 A:8,11 B:7,10 C:5,12 D:6,9【問題3】
4隅の数を1〜12の中の連続した4数とし、問題1と同様に小さい順から右回りに数を配置する場合、問題1と同じ考え方で下記のような解が求められます。
5 A 6
B C
8 D 7
として
下記とそれぞれのB,Cを入れ替えた4通り。
A:4,11 B:1,12 C:3,10 D:2,9 A:3,12 B:2,11 C:4,9 D:1,10
9 A 10 B C 12 D 11とした場合
連続しない4数とした場合、小さい順から右回りに数を配置する条件を残して、下記解があります。
1 A 4 B C 10 D 7として
A:8,12 B:3,11 C:5,9 D:2,6 A:9,11 B:2,12 C:6,8 D:3,5連続しない場合、上記の他、上記の対称位置にある組み合わせ以外にも複数の解があるようです。
何らかの対称性がある場合、解が判りやすいようですが、対称性がない場合に解があるのかどうかまで考えが及んでおりません。
【おまけ】
N=97として
(-97+98+99)×100×(101+102-103)=1000000
◆鹿児島県 ともひろ さんからの解答
プログラム(C言語)、および出力結果
解答を示すため、下図のように□の部分をa〜hとする。+−+−+−+−+
|1|a|b|2|
+−+−+−+−+
|c| |g|
+−+ +−+
|d| |h|
+−+−+−+−+
|3|e|f|4|
+−+−+−+−+
【問題1】
解答例
a= 7 , b=12 , c= 8 , d=10 , e= 6 , f= 9 , g= 5 , h=11 (L=22)+−+−+−+−+
|1|7|12|2|
+−+−+−+−+
|8| |5|
+−+ +−+
|10| |11|
+−+−+−+−+
|3|6|9|4|
+−+−+−+−+
【問題2】
解は「3パターン」ある。
なお、各辺の和は「22」のみ。
a〜hまでに数字が入る場合、48パターン存在する。
【問題1】の解答例から、一辺に含まれる数字の入れ替えを考慮する。
例えば、
a= 7 , b=12 , c= 8 , d=10 , e= 6 , f= 9 , g= 5 , h=11 (L=22)
a= 7 , b=12 , c= 8 , d=10 , e= 6 , f= 9 , g=11 , h= 5 (L=22)
2 x 2 x 2 x 2 = 16パターン存在して、これを同一パターンとみなすから
48 / 16 = 3
(1) a= 7 , b=12 , c= 8 , d=10 , e= 6 , f= 9 , g= 5 , h=11 (L=22)+−+−+−+−+
|1|7|12|2|
+−+−+−+−+
|8| |5|
+−+ +−+
|10| |11|
+−+−+−+−+
|3|6|9|4|
+−+−+−+−+
(2) a= 8 , b=11 , c= 6 , d=12 , e= 5 , f=10 , g= 7 , h= 9 (L=22)+−+−+−+−+
|1|8|11|2|
+−+−+−+−+
|6| |7|
+−+ +−+
|12| |9|
+−+−+−+−+
|3|5|10|4|
+−+−+−+−+
(3) a= 9 , b=10 , c= 6 , d=12 , e= 7 , f= 8 , g= 5 , h=11 (L=22)+−+−+−+−+
|1|9|10|2|
+−+−+−+−+
|6| |5|
+−+ +−+
|12| |11|
+−+−+−+−+
|3|7|8|4|
+−+−+−+−+
【問題3】
連続数であるならば、出題されている数字は「1〜12」であり、
この問題の解答のパターンの各数値にそれぞれN加算して、
一辺の和(22+4N)となる。可能。
◆ 問題へもどる
◆ 今週の問題へ