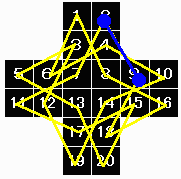
仧峀搰導丂惔愳丂堢抝 偝傫偐傜偺夝摎
亂栤戣侾亃
俀仺俋仺18仺16仺俉仺17仺11仺俈仺15仺20仺
13仺俆仺俁仺12仺19仺14仺10仺係仺俇仺侾
亂偍傑偗侾亃
偡傋偰壜擻丅
弌敪揰暿偺夝偺屄悢偼 34 34
10 10
34 10 4 4 10 34
34 10 4 4 10 34
10 10
34 34慡寢壥偼偙偪傜偱偡丅
亂偍傑偗俀亃
34捠傝
寢壥偼偙偪傜偱偡丅
仧垽抦導丂Y.M.Ojisan 偝傫偐傜偺夝摎
亂栤戣侾亃
俀仺俈仺11仺17仺15仺20仺13仺俆仺俁仺12仺
19仺14仺10仺係仺俇仺侾仺俉仺16仺18仺俋

亂偍傑偗侾亃
晄壜擻埵抲偼側偄丅
佹丂栤戣侾偺夝摎偵偍偄偰丄俋偐傜俀偵堏摦壜擻偱偁傞丅
懄偪儖乕僾偵側偭偰偄傞偺偱偳偐傜偱傕巒傔傜傟傞丅
側偍丄偍傑偗俀偺慡扵嶕偺寢壥丄儖乕僾夝偼,僷僞乕儞偲偰偟偰偼栤戣侾夝偺侾偲偍傝偱偁傞偙偲偑敾偭偨丅
亂偍傑偗俀亃
俁係捠傝丅丂乮偟傜傒偮傇偟俹俠夝乯
場傒偵丂係偐傜偼侾侽捠傝丄
俉偐傜偼慡晹儖乕僾偱係捠傝偱偁傞丅
扵嶕寢壥
2仺 9仺18仺 7仺11仺17仺15仺20仺13仺 5仺 3仺12仺19仺14仺10仺 4仺 6仺 1仺 8仺16仺Open 2仺 9仺18仺16仺 8仺17仺11仺 7仺15仺20仺 13仺 5仺 3仺12仺19仺14仺10仺 4仺 6仺 1仺Open 2仺 9仺18仺16仺 8仺 1仺 6仺17仺11仺 7仺 15仺20仺13仺 5仺 3仺12仺19仺14仺10仺 4仺Open 2仺 9仺18仺16仺 8仺 1仺 6仺17仺11仺 7仺 15仺20仺13仺 4仺10仺14仺19仺12仺 3仺 5仺Open 2仺 9仺18仺16仺 8仺 1仺 6仺17仺11仺 7仺 15仺 4仺10仺14仺19仺12仺 3仺 5仺13仺20仺Open 2仺 9仺18仺16仺 8仺 1仺 6仺 4仺10仺14仺 19仺12仺 3仺 5仺13仺20仺15仺17仺11仺 7仺Close 2仺 9仺18仺16仺 8仺 1仺 6仺 4仺10仺14仺 19仺12仺 3仺 5仺13仺20仺15仺 7仺11仺17仺Open 2仺 9仺13仺20仺15仺17仺11仺 7仺18仺16仺 8仺 1仺 6仺 4仺10仺14仺19仺12仺 3仺 5仺Open 2仺 9仺13仺 5仺 3仺12仺19仺14仺10仺 4仺 6仺 1仺 8仺16仺18仺 7仺11仺17仺15仺20仺Open 2仺 9仺 3仺12仺19仺14仺10仺 4仺 6仺 1仺 8仺16仺18仺 7仺11仺17仺15仺20仺13仺 5仺Open 2仺 9仺 3仺 5仺13仺20仺15仺17仺11仺 7仺 18仺12仺19仺14仺10仺 4仺 6仺 1仺 8仺16仺Open 2仺 9仺 3仺 5仺13仺20仺15仺17仺11仺 7仺 18仺16仺 8仺12仺19仺14仺10仺 4仺 6仺 1仺Open 2仺 9仺 3仺 5仺13仺20仺15仺17仺11仺 7仺 18仺16仺 8仺 1仺 6仺 4仺10仺14仺19仺12仺Open 2仺 9仺 3仺 5仺13仺20仺15仺 7仺11仺17仺 6仺 1仺 8仺16仺18仺12仺19仺14仺10仺 4仺Open 2仺 9仺 3仺 5仺13仺20仺15仺 7仺11仺17仺 6仺 4仺10仺14仺19仺12仺18仺16仺 8仺 1仺Open 2仺 9仺 3仺 5仺13仺20仺15仺 7仺11仺17仺 8仺16仺18仺12仺19仺14仺10仺 4仺 6仺 1仺Open 2仺 9仺 3仺 5仺13仺20仺15仺 7仺11仺17仺 8仺 1仺 6仺 4仺10仺14仺19仺12仺18仺16仺Open 2仺 9仺 3仺 5仺13仺20仺15仺 4仺10仺14仺 19仺12仺18仺 7仺11仺17仺 6仺 1仺 8仺16仺Open 2仺 9仺 3仺 5仺13仺20仺15仺 4仺10仺14仺 19仺12仺18仺16仺 8仺 1仺 6仺17仺11仺 7仺Close 2仺 9仺 3仺 5仺13仺20仺15仺 4仺10仺14仺 19仺12仺 8仺16仺18仺 7仺11仺17仺 6仺 1仺Open 2仺 9仺 3仺 5仺13仺20仺15仺 4仺10仺14仺 19仺12仺 8仺 1仺 6仺17仺11仺 7仺18仺16仺Open 2仺 9仺 3仺 5仺13仺 4仺10仺14仺19仺12仺 18仺16仺 8仺 1仺 6仺17仺11仺 7仺15仺20仺Open 2仺 7仺11仺17仺 6仺 1仺 8仺16仺18仺12仺 19仺14仺10仺 4仺15仺20仺13仺 5仺 3仺 9仺Close 2仺 7仺11仺17仺 6仺 1仺 8仺16仺18仺12仺 19仺14仺10仺 4仺15仺20仺13仺 9仺 3仺 5仺Open 2仺 7仺11仺17仺 6仺 1仺 8仺16仺18仺 9仺 13仺20仺15仺 4仺10仺14仺19仺12仺 3仺 5仺Open 2仺 7仺11仺17仺 6仺 1仺 8仺16仺18仺 9仺 13仺 5仺 3仺12仺19仺14仺10仺 4仺15仺20仺Open 2仺 7仺11仺17仺 6仺 1仺 8仺16仺18仺 9仺 3仺12仺19仺14仺10仺 4仺15仺20仺13仺 5仺Open 2仺 7仺11仺17仺 6仺 1仺 8仺16仺18仺 9仺 3仺 5仺13仺20仺15仺 4仺10仺14仺19仺12仺Open 2仺 7仺11仺17仺 6仺 1仺 8仺12仺19仺14仺 10仺 4仺15仺20仺13仺 5仺 3仺 9仺18仺16仺Open 2仺 7仺11仺17仺15仺20仺13仺 5仺 3仺 9仺 18仺12仺19仺14仺10仺 4仺 6仺 1仺 8仺16仺Open 2仺 7仺11仺17仺15仺20仺13仺 5仺 3仺 9仺 18仺16仺 8仺12仺19仺14仺10仺 4仺 6仺 1仺Open 2仺 7仺11仺17仺15仺20仺13仺 5仺 3仺 9仺 18仺16仺 8仺 1仺 6仺 4仺10仺14仺19仺12仺Open 2仺 7仺11仺17仺15仺20仺13仺 5仺 3仺12仺 19仺14仺10仺 4仺 6仺 1仺 8仺16仺18仺 9仺Close 2仺 7仺11仺17仺15仺20仺13仺 9仺18仺16仺 8仺 1仺 6仺 4仺10仺14仺19仺12仺 3仺 5仺Open 4仺10仺14仺19仺12仺18仺16仺 8仺 1仺 6仺 17仺11仺 7仺15仺20仺13仺 5仺 3仺 9仺 2仺Open 4仺10仺14仺19仺12仺18仺16仺 8仺 1仺 6仺 17仺11仺 7仺 2仺 9仺 3仺 5仺13仺20仺15仺Close 4仺10仺14仺19仺12仺18仺16仺 8仺 1仺 6仺 17仺15仺20仺13仺 5仺 3仺 9仺 2仺 7仺11仺Open 4仺10仺14仺19仺12仺 3仺 5仺13仺20仺15仺 17仺11仺 7仺 2仺 9仺18仺16仺 8仺 1仺 6仺Close 4仺10仺14仺19仺12仺 3仺 5仺13仺20仺15仺 17仺 6仺 1仺 8仺16仺18仺 9仺 2仺 7仺11仺Open 4仺10仺14仺19仺12仺 3仺 5仺13仺20仺15仺 7仺11仺17仺 6仺 1仺 8仺16仺18仺 9仺 2仺Open 4仺10仺14仺19仺12仺 3仺 5仺13仺20仺15仺 7仺 2仺 9仺18仺16仺 8仺 1仺 6仺17仺11仺Open 4仺10仺14仺 6仺 1仺 8仺16仺18仺 9仺 2仺 7仺11仺17仺15仺20仺13仺 5仺 3仺12仺19仺Open 4仺15仺20仺13仺 5仺 3仺 9仺 2仺 7仺11仺 17仺 6仺 1仺 8仺16仺18仺12仺19仺14仺10仺Close 4仺 6仺 1仺 8仺16仺18仺 9仺 2仺 7仺11仺 17仺15仺20仺13仺 5仺 3仺12仺19仺14仺10仺Close 8仺16仺18仺12仺19仺14仺10仺 4仺15仺20仺 13仺 5仺 3仺 9仺 2仺 7仺11仺17仺 6仺 1仺Close 8仺16仺18仺 9仺 2仺 7仺11仺17仺15仺20仺 13仺 5仺 3仺12仺19仺14仺10仺 4仺 6仺 1仺Close 8仺 1仺 6仺17仺11仺 7仺 2仺 9仺 3仺 5仺 13仺20仺15仺 4仺10仺14仺19仺12仺18仺16仺Close 8仺 1仺 6仺 4仺10仺14仺19仺12仺 3仺 5仺 13仺20仺15仺17仺11仺 7仺 2仺 9仺18仺16仺Close
仧媨忛導丂傾儞僷儞儅儞 偝傫偐傜偺夝摎
亂栤戣侾亃
俀仺俋仺18仺16仺俉仺17仺11仺俈仺15仺20仺
13仺俆仺俁仺12仺19仺14仺10仺係仺俇仺侾
亂偍傑偗侾亃
偳偺弌敪揰傕壜擻偱偡丅
棟桼偼
1-8-16-18-9-2-7-11-17-15-20-13-5-3-12-19-14-10-4-6-1
偺儖乕僾偼廳暋側偟偱偡傋偰偺儅僗栚傪捠偭偨偨傔丄
偙偺儖乕僾偺拞丄弌敪揰偵偟偨偄儅僗栚偲偺偮側偑傝慄堦杮傪徚偣偽丄
巆傝偺慄傪扝偭偰峴偔偲嵟屻偺儅僗栚(偮側偑傝慄偺傕偆曅曽偺儅僗栚)偵扝傝拝偒傑偡丅
傑偨 OX
XO
OXOXOX
XOXOXO
OX
XO
偲偄偆晽偵彂偒丄婏嬼傪峫椂偟偰
X偺廤崌亖{1,4,5,7,9,12,14,16,17,20}偱巒傑傞応崌
O偺廤崌亖{2,3,6,8,10,11,13,15,18,19}偱廔傢傜側偄偲偄偗傑偣傫丅
傑偨媡偵O偱巒傑傞偲X偱廔傢傞偲偄偆偙偲傕尵偊傑偡丅
亂偍傑偗俀亃
a_{ij}= 1 傕偟i偐傜j偵堏摦偱偒傞,
a_{ij}= 0 傕偟i偐傜j偵堏摦偱偒側偄
偲掕媊偡傞偲
A={aa_{ij}}偼堏摦偡傞峴楍傪昞偟丄
A=|0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0| |0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0| |0 0 0 0 1 0 0 0 1 0 0 1 0 1 0 0 0 0 0 0| |0 0 0 0 0 1 0 0 0 1 0 0 1 0 1 0 0 0 0 0| |0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0| |1 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0| |0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0 0| |1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 0 0| |0 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0| |0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0| |0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0| |0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 1 0| |0 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1| |0 0 1 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 1 0| |0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 1| |0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0| |0 0 0 0 0 1 0 1 0 0 1 0 0 0 1 0 0 0 0 0| |0 0 0 0 0 0 1 0 1 0 0 1 0 0 0 1 0 0 0 0| |0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0| |0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0|偱偡丅 媮傔偨偄捠傝悢(N_1)偼
N_1=儼_{慡偰堎側傞r_i亗侾}a_{1,r_2}a_{r_2,r_3}...a_{r_19,r_20}
側偺偱偐側傝偺寁嶼検偱偡丅
(儅僗栚傪僌儔僼偺揰偵偟偰丄n揰偑偁傞応崌丄(n-1)!屄偺抣偺憤榓偑昁梫偱偡)丅
B={1,2,...,20}亖儅僗栚偺廤崌偲偟傑偡丅
Q_B={Q_{(i,j),B}}丄
Q_{(i,j),B}偼B忋偱弌敪揰偼i偱廔揰偼j偱偁傞廳暋柍偟偱慡偰偺揰傪捠傞宱楬悢偲偡傞偲丄
Q_{(i,j),B}亖儼_{k亗i} a_{i,k} Q_{(k,j),B(i)}偺慟壔幃偱昞偝傟丄
偙偙偱B(i)=B-{i}偱偡丅
C亖A-DiagonalMatrix(A), C(i)=C偺i斣栚偺峴偲偟丄
(偙偺栤戣偱偼DiagonalMatrix(A)亖侽偨傔丄C亖A)
A偼n*n僒僀僘偺峴楍偲偡傞偲
Q_{B}= | C(1)Q_{B(1)} |
| C(2)Q_{B(2)} |
| : |
| C(n)Q_{B(n)} | 偑惉傝棫偪傑偡偑丄偙偺幃偱寁嶼偡傞偺傕偐側傝寁嶼検偑昁梫偱偡偺偱丄暿偺曽朄偱寁嶼偟偰傒傑偡丅
傑偢,P_r (i,j)=B忋偱弌敪揰偼i偱廔揰偼j偱廳暋側偟偱r偺挿偝偺宱楬悢
(Number of Path)偱丄P_r={P_r(i,j)}偲掕媊偟傑偡丅
傑偨
L_r(i,j)=0 傕偟i亗j
L_r(i,j)=弌敪揰偲廔揰偼i偱廳暋側偟偱r偺挿偝偺儖乕僾悢(Number of Loop)偱丄
L_r={L_r(i,j)}偲掕媊偟傑偡丅
掕棟丗P_1=A-L_1偱昞偝傟丄偝傜偵P_k偼P_1,P_2,....,P_{k-1}偱昞偡偙偲偑偱偒傑偡丅(徹柧徣棯)
椺偲偟偰 P_1=A-L_1,
P_2=P_12-L_2
P_3=P_2P_1-L_3-P_1*L_2+P_1
P_4=P_3P_1-L_4-P_1L_3+3P_1*P_2-P_2L_2+P_2
P_5=P_4P_1-L_5-P_1L_4+3P_1*P_3+3P_1*P_2(2)+3P_1(P_1*P_2)-3L_3+P_3-P_3*L_2-P_2L_3-4P_1P_2 P_6=P_5P_1-L_6-P_1L_5+3P_1*P_4+6P_1*P_2*P_3-8P_1*(P_1(P_1*P_2))-8P_1*((P_1*P_2)P_1)-P_2L_4+P_2(3)-4P_2(2)+3P_2+3P_1(P_1*P_3)+3P_1(P_1*P_2(2))-3L_4+21P_1*P_2-P_4L_2-P_3L_3+3P_2(P_1*P_2)-3P_1(P_1*P_2)+3L_3-6I*(P_1(P_2(2)))-4P_1L_3+P_4*偺墘嶼巕偼丄A={a_{ij}},B_{b_{ij}}偺応崌丄C亖A*B亖{a_{ij}b_{ij}}偲掕媊偟傑偡丅
D(X)偼惓曽峴楍偐傜惓曽峴楍傊偺娭悢偱D(X)亖I*X偱偡丅
傑偨
L_k=D(P_{k-1}P_1)=D(P_1P_{k-1})=I*(P_{k-1}P_1)=I*(P_1P_{k-1})偱媮傑傝傑偡丅
偪側傒偵忋婰偺P_k偺幃偼丄 (k-1)偺挿偝偺宱楬(P_{k-1})僾儔僗1偺挿偝偺宱楬(P_{1})偐傜峫偊偰摼傜傟偨幃偱偡丅
摨偠傛偆偵丄P_k偺幃傪(k-2)偲俀偺挿偝偺宱楬偐傜峔惉偝傟傞偲峫偊傞偲傑偨暿偺幃偑摼傜傟傑偡丅
偙偺栤戣丄n=20偱偁傞偨傔丄P_{19}傑偱偺幃偑傢偐傞偲媮傔偨偄宱楬悢偑媮傑傝傑偡丅
P_{19}偺幃傑偱媮傔傞偺偵崲擄偱傕偁傝傑偡偑丄懠偺椶帡栤戣偵傕巊偊傞
(Derive Once Calculate Anywhere)偺偱媮傔傞壙抣偑偁傞偲巚偄傑偡丅
傑偨P_1,...,P_{19}偺幃偱寁嶼偡傞偙偲偵傛偭偰丄慡偰偺i偐傜j傑偱偺偡傋偰偺挿偝偺廳暋側偟偺宱楬悢丄傑偨偼i傪捠傞廳暋柍偟偺儖乕僾悢傕傢偐傝傑偡丅
偝傜偵丄働乕僗傪暘偗傞偙偲偵傛偭偰丄P_{11}傑偱傢偐傟偽丄偙偺栤戣傪夝偔偙偲偑偱偒傑偡丅
椶帡栤戣偲偟偰乽塃愜嬛巭偺暯埨嫗乿栤戣傗乽崱廡偺栤戣僔儕乕僘乿偵偱偰偒偨宱楬悢偵娭偡傞栤戣側偳偑嫇偘傜傟傑偡丅
乽塃愜嬛巭偺暯埨嫗乿栤戣偺応崌偼奿巕揰偲奿巕揰傪寢傇摴楬傪僌儔僼偺揰偲偟偰峫偊, 師偺摴楬偵恑傔傞偐偳偆偐傪侾偲侽偱昞偟偰峫偊傞偲丄
m(m-1)+n(n-1)揰偺桳岦僌儔僼(Directed Graph)偺廳暋柍偟偺宱楬悢偺栤戣偵曄傢傝傑偡丅
偨偩偟丄偙偺僌儔僼偼桳岦僌儔僼偱偁傞偨傔丄P_i 偺幃傪巊偆偺偱偼側偔丄桳岦僌儔僼偺偨傔偺Q_i偺幃傪峫偊側偗傟偽側傝傑偣傫丅
Q_{m(m-1)+n(n-1)-1}傑偱偺幃偑夝傟偽丄宱楬悢偑寁嶼偱偒傑偡丅
(幚嵺丄偙偺栤戣偺惈幙偵傛傝丄P_{m(m-1)+n(n-1)-1}傑偱偺幃偑昁梫側偄偼偢偱偡丅)
仧搶嫗搒丂You.O 偝傫偐傜偺夝摎
傑偢亂偍傑偗俀亃偐傜丅
俀侽僐偺儅僗栚偺偆偪椬愙偡傞儅僗栚偺悢偑俀丆俁丆係偱偁傞儅僗栚偺廤崌傪偦傟偧傟俙丆俛丆俠偲偡傞丅
偡側傢偪丄
俙亖乷侾丆俀丆俆丆10丆11丆16丆19丆20乸丆
俛亖乷俁丆係丆俇丆俋丆12丆15丆17丆18乸丆
俠亖乷俈丆俉丆13丆14乸偱偁傞丅
傑偨丄倀亖俙伨俛伨俠亖乷侾丆俀丆俁丆丒丒丒丆20乸偲偟偰偍偔丅
師偵丄儅僗栚鶣偐傜儅僗栚倞傊僫僀僩偑侾夞偺摦偒偱堏摦偱偒傞偲偒丄鶣偲倞偼乽寢偽傟偰偄傞乿偲掕媊偟丄
偙傟傪乬鶣丵倞乭偱昞傢偡偙偲偵偟偰偍偔丅
摉慠偺偙偲側偑傜丄偙偺掕媊偵偼岎姺朄懃偑惉傝棫偮丅
偙偺偲偒丄
(1)俙偺擟堄偺梫慺倎偵懳偟偰丄倎丵倯丆倎丵倰傪枮偨偡俛丆俠偺梫慺倯丆倰偑偦傟偧傟偨偩侾偮偢偮懚嵼偟丄倎丵倫傪枮偨偡俙偺梫慺倫偼懚嵼偟側偄丅
(2)俛偺擟堄偺梫慺倐偵懳偟偰丄倐丵倫丆倐丵倰傪枮偨偡俙丆俠偺梫慺倫丆倰偑偦傟偧傟偨偩侾偮偢偮懚嵼偟丄倐丵倯傪枮偨偡俛偺梫慺倯乮倯亗倐乯偼俀偮懚嵼偡傞丅
(3)俠偺擟堄偺梫慺們偵懳偟偰丄們丵倫丆們丵倯傪枮偨偡俙丆俛偺梫慺倫丆倯偑偦傟偧傟俀偮偢偮懚嵼偟丄們丵倰傪枮偨偡俠偺梫慺倰偼懚嵼偟側偄丅
僫僀僩偑堏摦偡傞儅僗栚偺斣崋傪弴偵暲傋偨悢楍傪峫偊傞偲丄偙偺栤戣偺夝偼師偺傛偆側宍偱昞偝傟傞丅
丂{Xi丟侽亝鶣亝19乸亖X0丆X1丆X2丆丒丒丒丆X19
偨偩偟
丒X0亖俀乮伕俙乯
丒擟堄偺鶣乮侽亝鶣亝19乯偵懳偟偰Xi伕倀
丒擟堄偺鶣乮侽亝鶣亝18乯偵懳偟偰Xi丵X(i+1)
丒擟堄偺鶣丆倞乮侽亝鶣亙倞亝19乯偵懳偟偰Xi亗Xj
偙偺偲偒
(1)傛傝丄Xi伕俙丆X(i+1)伕俙傪枮偨偡鶣乮侽亝鶣亝18乯偼懚嵼偟側偄丅丂丂丂丂丂丂丒丒丒(4)
(3)傛傝丄Xi伕俠丆X(i+1)伕俠傪枮偨偡鶣乮侽亝鶣亝18乯偼懚嵼偟側偄丅丂丂丂丂丂丂丒丒丒(5)
(1)傛傝丄Xi伕俛丆X(i+1)伕俙丆X(i+2)伕俛傪枮偨偡鶣乮侽亝鶣亝17乯偼懚嵼偟側偄丅丒丒丒(6)
(1)傛傝丄Xi伕俠丆X(i+1)伕俙丆X(i+2)伕俠傪枮偨偡鶣乮侽亝鶣亝17乯偼懚嵼偟側偄丅丒丒丒(7)
(2)傛傝丄Xi伕俙丆X(i+1)伕俛丆X(i+2)伕俙傪枮偨偡鶣乮侽亝鶣亝17乯偼懚嵼偟側偄丅丒丒丒(8)
(2)傛傝丄Xi伕俠丆X(i+1)伕俛丆X(i+2)伕俠傪枮偨偡鶣乮侽亝鶣亝17乯偼懚嵼偟側偄丅丒丒丒(9)
乮嘥乯X19伕俛傑偨偼X19伕俠偺偲偒
忋偺悢楍乷Xi乸偱俙偺梫慺傪弌偰偔傞弴偵a1丆a2丆a3丆丒丒丒丆a8丄俛偺梫慺傪弌偰偔傞弴偵b1丆b2丆b3丆丒丒丒丆b8丄俠偺梫慺傪弌偰偔傞弴偵c1丆c2丆c3丆c4偲偡傞丅
a1丆a2丆a3丆丒丒丒丆a8丆b1丆b2丆b3丆丒丒丒丆b8丆c1丆c2丆c3丆c4偺暲傃曽偼師偺傛偆偵乮a8埲崀偺暲傃曽偵傛偭偰乯応崌暘偗偝傟傞丅
傾乯X18伕俙丆X19伕俠偺応崌
a1,b1,b2,a2,c1,a3,b3,b4,a4,c2,a5,b5,b6,a6,c3,a7,b7,b8,a8,c4
僀乯X17伕俙丆X18伕俛丆X19伕俛偺応崌
a1,c1,a2,b1,b2,a3,c2,a4,b3,b4,a5,c3,a6,b5,b6,a7,c4,a8,b7,b8
偙偙偱丄侽亝鶣亝16偵懳偡傞乮Xi乮伕俙乯丆X(i+1)乮伕俛乯丆X(i+2)乮伕俛乯丆X(i+3)乮伕俙乯乯偺慻偲侽亝鶣亝17偵懳偡傞乮Xi乮伕俙乯丆X(i+1)乮伕俠乯丆X(i+2)乮伕俙乯乯偺慻傪峫偊傞偲丄
丂乮Xi乮伕俙乯丆X(i+1)乮伕俛乯丆X(i+2)乮伕俛乯丆X(i+3)乮伕俙乯乯 亖乮侾丆俇丆係丆10乯丆乮侾丆俇丆17丆11乯丆乮俀丆俋丆俁丆俆乯丆乮俀丆俋丆18丆16乯丆 丂乮俆丆俁丆俋丆俀乯丆乮俆丆俁丆12丆19乯丆乮10丆係丆俇丆侾乯丆乮10丆係丆15丆20乯丆 丂乮11丆17丆俇丆侾乯丆乮11丆17丆15丆20乯丆乮16丆18丆俋丆俀乯丆乮16丆18丆12丆19乯丆 丂乮19丆12丆俁丆俆乯丆乮19丆12丆18丆16乯丆乮20丆15丆係丆10乯丆乮20丆15丆17丆11乯 丂乮Xi乮伕俙乯丆X(i+1)乮伕俠乯丆X(i+2)乮伕俙乯乯 亖乮侾丆俉丆16乯丆乮俀丆俈丆11乯丆乮俆丆13丆20乯丆乮10丆14丆19乯丆 丂乮11丆俈丆俀乯丆乮16丆俉丆侾乯丆乮19丆14丆10乯丆乮20丆13丆俆乯偙傟傪梡偄偰乮a1丆a2丆a3丆丒丒丒丆a8乯偺慻傪寛掕偡傞偲丄
丂傾乯偺応崌 丂丂乮a1丆a2丆a3丆丒丒丒丆a8乯亖乮俀丆俆丆20丆10丆19丆16丆侾丆11乯丆乮俀丆16丆侾丆10丆19丆俆丆20丆11乯 丂僀乯偺応崌 丂丂乮a1丆a2丆a3丆丒丒丒丆a8乯亖乮俀丆11丆侾丆16丆19丆10丆20丆俆乯丆乮俀丆11丆20丆俆丆19丆10丆侾丆16乯偙傟傜係偮偺偄偢傟偺応崌偵傕丄b1丆b2丆b3丆丒丒丒丆b8偍傛傃c1丆c2丆c3丆c4偼偦傟偧傟堦堄揑偵掕傑傝丄a1丆a2丆a3丆丒丒丒丆a8偲崌傢偣偨俀侽僐偺悢偼偡傋偰堎側傞丅
傾乯丒丒丒俀捠傝
僀乯丒丒丒俀捠傝
僂乯X18伕俙丆X19伕俛偺応崌
乮嘦乯偺峫偊曽傪揔梡偡傞丅
X1伕乷俈丆俋乸丆X19伕乮俛伩俤乯亖乷係丆俋丆12丆17乸偱偁傝丄
亀倶丵倷乮倶伕倀丆倷伕倀乯傪枮偨偡俁俀偺慻偺偆偪梡偄傜傟側偄侾俁慻傪偡傋偰彂偒弌偡偲丄
偦偺拞偵X0乮亖俀乯偑侾僐丆X19乮伕俛乯偑俁僐丄X19埲奜偺俛偺梫慺偍傛傃俠偺梫慺偑奺俀僐偢偮尰傟傞亁偼偢偱偁傞丅
乮侾乯X1亖俈偺応崌
乮偁乯X19亖係偺偲偒
倶丵倷乮倶伕倀丆倷伕倀乯傪枮偨偡俁俀偺慻偺偆偪丄乮鶣乯偺乮倶丆倷乯亖乮俀丆俋乯丆乮鶥乯偺乮倶丆倷乯亖乮係丆俇乯丆乮係丆15乯偍傛傃乮鶦乯偺俉慻偡傋偰偑梡偄傜傟側偄丅
梡偄傜傟側偄慻偼偁偲俀偮偱偁傞偑丄巆傝偺慻偺拞偐傜俀慻傪偳偺傛偆偵慖傫偱傕丄忋偺亀丂亁撪偺忦審傪枮偨偝側偄丅
乮偄乯X19亖俋偺偲偒
丂乮偁乯偲摨條丄亀丂亁偺忦審傪枮偨偡侾俁慻偺慖傃曽偼懚嵼偟側偄丅
乮偆乯X19亖12偺偲偒
丂乮鶣乯偺乮倶丆倷乯亖乮俀丆俋乯丆乮鶥乯偺乮倶丆倷乯亖乮俁丆12乯丆乮12丆18乯偍傛傃乮鶦乯偺俉慻偡傋偰偑梡偄傜傟側偄丅
亀丂亁偺忦審傪枮偨偡巆傝俀慻偺慖傃曽偼丄
乮鶥乯偺乮倶丆倷乯亖乮係丆俇乯丆乮15丆17乯傑偨偼乮倶丆倷乯亖乮係丆15乯丆乮俇丆17乯偺俀捠傝丅
偙偺偦傟偧傟偵偮偄偰侾捠傝偢偮偺僫僀僩偺恑傔曽偑懚嵼偡傞丅
乮偊乯X19亖17偺偲偒
丂乮偁乯偲摨條丄亀丂亁偺忦審傪枮偨偡侾俁慻偺慖傃曽偼懚嵼偟側偄丅
乮俀乯X1亖俋偺応崌
丂摨偠傛偆偵峫偊偰丄X19亖係偺偲偒俀捠傝丄X19亖12偺偲偒侾捠傝丆X19亖17偺偲偒侾捠傝丄寁係捠傝偺僫僀僩偺恑傔曽偑懚嵼偡傞丅
傾乯偺俀捠傝丄僀乯偺俀捠傝丄僂乯偺俇捠傝傪崌傢偣偰丄乮嘥乯偺応崌偺僫僀僩偺恑傔曽偼侾侽捠傝丅
乮嘦乯X19伕俙偺偲偒
俢亖乷俀丆俁丆俇丆俉丆10丆11丆13丆15丆18丆19乸
俤亖乷侾丆係丆俆丆俈丆俋丆12丆14丆16丆17丆20乸
偲偡傞偲丄僫僀僩偺堏摦偺惈幙偐傜丄擟堄偺倣乮侽亝倣亝俋乯偵懳偟偰丄
丂X(2m)伕俢丆X(2m+1)伕俤偲側傞丅備偊偵丄
丂X(19)伕乮俙伩俤乯亖乷侾丆俆丆16丆20乸
偲偙傠偱(1)乣(3)傛傝丄
(10)俙偺擟堄偺梫慺倎偵懳偟偰丄倎丵倶傪枮偨偡倀偺梫慺倶偑俀偮懚嵼偡傞丅
(11)俛偺擟堄偺梫慺倐偵懳偟偰丄倐丵倶傪枮偨偡倀偺梫慺倶偑係偮懚嵼偡傞丅
(12)俠偺擟堄偺梫慺們偵懳偟偰丄們丵倶傪枮偨偡倀偺梫慺倶偑係偮懚嵼偡傞丅
堦曽丄悢楍乷Xi乸偼師偺傛偆側惈幙傪帩偭偰偄傞丅
丒X1偼X0丵倶傪枮偨偡倀偺梫慺倶偺偆偪偺侾偮偱偁傞丅
丒擟堄偺鶣乮侾亝鶣亝18乯偵懳偟偰丄X(i-1)偲X(i+1)偼Xi丵倶傪枮偨偡憡堎側傞倀偺俀偮偺梫慺偱偁傞丅
丒X18偼X19丵倶傪枮偨偡倀偺梫慺倶偺偆偪偺侾偮偱偁傞丅
傑偨丄倶丵倷傪枮偨偡倀偺乮憡堎側傞乯梫慺乮倶丆倷乯偼壓偺俁俀慻偱偁傝丄偦偺偆偪侾俋慻偑悢楍乷Xi乸傪峔惉偡傞偺偵梡偄傜傟傞偐傜丄巆傝偺侾俁慻偼梡偄傜傟側偄偙偲偲側傞丅
乮鶣乯倶伕俙丆倷伕俛偺応崌 丂乮倶丆倷乯亖乮侾丆俇乯丆乮俀丆俋乯丆乮俆丆俁乯丆乮10丆係乯丆 丂丂丂丂丂丂丂乮11丆17乯丆乮16丆18乯丆乮19丆12乯丆乮20丆15乯 乮鶤乯倶伕俙丆倷伕俠偺応崌 丂乮倶丆倷乯亖乮侾丆俉乯丆乮俀丆俈乯丆乮俆丆13乯丆乮10丆14乯丆 丂丂丂丂丂丂丂乮11丆俈乯丆乮16丆俉乯丆乮19丆14乯丆乮20丆13乯 乮鶥乯倶伕俛丆倷伕俛偺応崌 丂乮倶丆倷乯亖乮俁丆俋乯丆乮俁丆12乯丆乮係丆俇乯丆乮係丆15乯丆 丂丂丂丂丂丂丂乮俇丆17乯丆乮俋丆18乯丆乮12丆18乯丆乮15丆17乯 乮鶦乯倶伕俛丆倷伕俠偺応崌 丂乮倶丆倷乯亖乮俁丆14乯丆乮係丆13乯丆乮俇丆14乯丆乮俈丆15乯丆 丂丂丂丂丂丂丂乮俈丆18乯丆乮俉丆12乯丆乮俉丆17乯丆乮俋丆13乯(10)乣(12)偍傛傃忋偱弎傋偨悢楍乷Xi乸偺惈幙偲
傾乯X1伕俠丆X18伕俠偺偲偒
偙偺偲偒丄忋偺乮鶤乯偺俉慻偡傋偰偑悢楍乷Xi乸偺峔惉偵梡偄傜傟傞偙偲偲(13)偐傜丄乮鶦乯偺俉慻偼偡傋偰梡偄傜傟側偄丅
傑偨丄X0亖俀偱偁傞偐傜丄乮鶣乯偺乮倶丆倷乯亖乮俀丆俋乯偼梡偄傜傟側偄丅
椺偲偟偰丄X19亖侾偺応崌傪峫偊傞偲丄乮鶣乯偺乮倶丆倷乯亖乮侾丆俇乯偼梡偄傜傟偢丄巆傝俁慻偺梡偄傜傟側偄慻傒崌傢偣偼偡傋偰乮鶥乯偵懏偡傞偙偲偵側傞偑丄(13)偺忦審傪枮偨偡傛偆偵丄乮鶥乯偺拞偐傜梡偄傜傟側偄俁慻傪慖傇偙偲偼偱偒側偄丅
X19亖俆偺応崌偵偼丄乮鶥乯偺俉慻偺慻傒崌傢偣偲(13)傪峫椂偡傞偲梡偄傜傟側偄慻傒崌傢偣偼師偺傛偆偵側傞丅
乮鶣乯偺乮倶丆倷乯亖乮俀丆俋乯丆乮俆丆俁乯丆乮鶦乯偺俉慻偡傋偰丆
乮鶥乯偺乵偁乶乮倶丆倷乯亖乮係丆俇乯丆乮12丆18乯丆乮15丆17乯傑偨偼
乵偄乶乮倶丆倷乯亖乮係丆15乯丆乮12丆18乯丆乮俇丆17乯
乵偁乶偺応崌
丂乷Xi乸亖俀丆俈丆11丆17丆俇丆侾丆俉丆16丆18丆俋丆俁丆12丆19丆14丆10丆係丆15丆20丆13丆俆
乵偄乶偺応崌
丂悢楍乷Xi乸傪偮偔傞偙偲偑偱偒側偄丅
乮X0偐傜弴偵寛掕偟偰備偔偲丄X7亖俆亖X19偲側傞乯
摨條偵偟偰丄X19亖16偺応崌偵侾捠傝偺摦偐偟曽偑偁傝丄X19亖20偺応崌偵偼摦偐偟曽偑側偄偙偲偑傢偐傞丅
偡側傢偪丄忦審傪枮偨偡応崌偑俀捠傝偁傞丅
僀乯X1伕俛丆X18伕俠偺偲偒
偙偺偲偒丄忋偺乮鶤乯偺乮倶丆倷乯亖乮俀丆俈乯偼乷Xi乸偺峔惉偵梡偄傜傟側偄偑丄偦傟埲奜偺俈慻偼梡偄傜傟傞丅
備偊偵(13)偐傜丄乮鶦乯偺俉慻偺偆偪偨偩侾慻偼梡偄傜傟丄偦傟埲奜偺俈慻偼偡傋偰梡偄傜傟側偄偙偲偑傢偐傞丅
(13)傪峫椂偡傞偲丄梡偄傜傟側偄侾俁慻偺慻傒崌傢偣偺拞偵乬俈乭偑偪傚偆偳俀夞尰傟傞偙偲偐傜丄乮鶦乯偺拞偱梡偄傜傟傞慻傒崌傢偣偼
乮倶丆倷乯亖乮俈丆15乯傑偨偼乮俈丆18乯偱偁傞偙偲偑傢偐傞丅
偝傜偵乮鶥乯偺俉慻偺慻傒崌傢偣偐傜丄X19亖侾丆20偺偲偒丄
偙偺慻傒崌傢偣偼乮倶丆倷乯亖乮俈丆15乯偵寛掕偟丄
X19亖俆丆16偺偲偒偼乮倶丆倷乯亖乮俈丆18乯偵寛掕偡傞偙偲偑傢偐傞丅
懠偺慻傒崌傢偣傕峫椂偟偰丄X19亖侾丆俆丆20偺偲偒奺侾捠傝偢偮丄X19亖16偺偲偒俁捠傝偺寁俇捠傝偺摦偐偟曽傪敪尒偡傞偙偲偑偱偒傞丅
僂乯X1伕俠丆X18伕俛偺偲偒
摨條偵偟偰丄X19亖侾丆16丆20偺偲偒奺侾捠傝偢偮丄X19亖俆偺偲偒俁捠傝偺寁俇捠傝偺摦偐偟曽偑偁傞偙偲偑傢偐傞丅
僄乯X1伕俛丆X18伕俛偺偲偒
摨條偵偟偰丄X19亖俆丆16丆20偺偲偒奺俀捠傝偢偮丄X19亖侾偺偲偒係捠傝偺寁侾侽捠傝偺摦偐偟曽偑偁傞偙偲偑傢偐傞丅
傾乯乣僄乯傑偱崌傢偣偰乮嘦乯偼俀係捠傝偺摦偐偟曽偑偁傞丅
乮嘥乯偺侾侽捠傝丄乮嘦乯偺俀係捠傝傪崌傢偣偰丄僫僀僩偺恑傔曽偼慡晹偱俁係捠傝丅
峫偊曽偑僀儅僀僠傛偔揱傢傜側偄偲巚偄傑偡偺偱曗懌傪偟偰偍偒傑偡丅
擟堄偺乮倶丆倷乯偺慻乮侾亝倶亙倷亝20乯偵偮偄偰丄俀揰倶丆倷偺娫傪僫僀僩偑侾夞偺摦偒偱堏摦壜擻側偲偒偺傒倶偲倷傪慄偱寢傫偩恾傪昤偔偲壓偺傛偆偵側傝傑偡丅
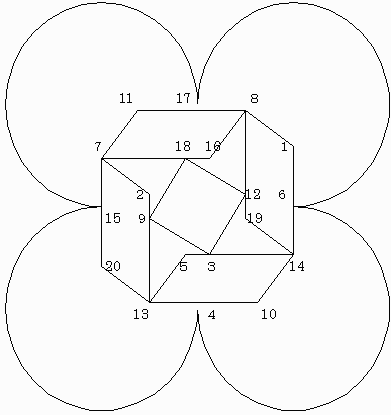
僫僀僩偑侾俋夞偺堏摦偱偨偳傞宱楬偼丄偙偺恾拞偺斣崋偺偮偄偨揰傪椉抂偵傕偮俁俀杮偺慄偺偆偪丄侾俋杮偺慄偱昞偝傟傑偡丅
偦偙偱丄僫僀僩偑捠傜側偄侾俁杮偺宱楬偺慖傃曽傪峫偊傞傢偗偱偡丅
俙偺梫慺偲側傞奺揰乮侾丆俀丆俆丆10丆11丆16丆19丆20乯偐傜偼偦傟偧傟俀杮丄俛偍傛傃俠偺梫慺偲側傞奺揰偐傜偼偦傟偧傟係杮偺宱楬偑弌偰偄傞傢偗偱偡偑丄僫僀僩偑摨偠揰傪廳暋偟偰捠傞偙偲側偔侾俋夞堏摦偟偨偲偒偺宱楬傪恾偵昞偡偲丄僗僞乕僩抧揰乮俀乯偲僑乕儖抧揰偐傜偼奺侾杮偢偮偺慄偑丄偦傟埲奜偺侾俉僐偺揰偐傜偼奺俀杮偢偮偺慄偑弌偰偄側偗傟偽側傝傑偣傫丅
偨偩偟丄僗僞乕僩丒僑乕儖抧揰埲奜偺侾俉僐偺揰偺偆偪偄偔偮偐偑師偺椺偺傛偆偵儖乕僾傪宍惉偟偰偟傑偆偙偲偑偁傞偺偱梫拲堄両
椺丏僫僀僩傪捠傜側偄侾俁杮偺宱楬傪師偺傛偆偵慖傇丅
俀亅俋丆俁亅俆丆俁亅14丆係亅13丆係亅15丆俇亅14丆俇亅17丆
俈亅15丆俈亅18丆俉亅12丆俉亅17丆俋亅13丆12亅18
偙偺偲偒丄巆傝偺侾俋杮偺宱楬偺偆偪偺侾俀杮偑丄
丂丂侾亅俇亅係亅10亅14亅19 丂丂乥丂丂丂丂丂丂丂丂丂 乥 丂丂俉亅16亅18亅俋亅俁亅12偲偄偆儖乕僾傪宍惉偟丄俀偐傜僗僞乕僩偡傞僫僀僩偺摦偒偼丄
俀亅俈亅11亅17亅15亅20亅13亅俆
偱廔傢偭偰偟傑偆丅
埲忋偺偙偲偵拲堄偡傟偽丄峫偊傜傟傞僫僀僩偺堏摦宱楬偼忋偺椺偺傛偆側応崌傪娷傔偰傕俇侽庬椶掱搙偵偁傜偐偠傔偟傏偭偰偍偔偙偲偑偱偒丄俹俠傪巊傢偢偵夝偔偙偲偑偱偒傑偡丅
帪娫偼傗偭傁傝偐偐傝傑偡偗偳偹丅
亂偍傑偗侾亃
忋偺亂偍傑偗俀亃偺夝摎偱弎傋偨乮俬乯偺応崌偺夝偼丄
X19丵X0乮亖俀乯傪枮偨偡丅偡側傢偪丄僫僀僩偼
X0丆X1丆X2丆丒丒丒丆X19丆X0丆X1丆X2丆丒丒丒
偲偄偆傛偆偵侾偐傜20傑偱偺偡傋偰偺儅僗栚傪侾偮偢偮廃婜揑偵堏摦偡傞偙偲偑偱偒傞丅
偄傑丄弌敪揰偺斣崋傪倠乮侾亝倠亝20乯偲偡傞偲丄
乷X0丆X1丆X2丆丒丒丒丆X19乸亖倀亖乷侾丆俀丆俁丆丒丒丒丆20乸偱偁傞偐傜丄
擟堄偺倠偺抣偵懳偟偰Xi亖倠偲側傞鶣偺抣乮侽亝鶣亝19乯偑昁偢偨偩侾偮懚嵼偡傞丅
偦偺抣傪値偲偡傞偲丄弌敪揰偑倠偺応崌偵偼丄
Xk丆X(k+1)丆丒丒丒丆X19丆X0丆X1丆X2丆丒丒丒丆X(k-1)
偲偄偆傛偆偵僫僀僩傪堏摦偡傟偽傛偄丅
偟偨偑偭偰丄偡傋偰偺儅僗栚傪堦夞偢偮捠偭偰恑傓偙偲偑晄壜擻側弌敪揰偼懚嵼偟側偄丅
椺偲偟偰丄乮嘥乯偺応崌偺夝偺侾偮乮偙傟偑亂栤戣侾亃偺夝摎偲偄偆偙偲偵偟偰偍偒傑偡乯
俀丆俋丆俁丆俆丆13丆20丆15丆係丆10丆14丆19丆12丆18丆16丆俉丆侾丆俇丆17丆11丆俈
傪傕偲偵偟偨偲偒丄16傪弌敪揰偲偟偨偲偒偺僫僀僩偺恑傔曽偼師偺傛偆偵側傝傑偡丅
16丆俉丆侾丆俇丆17丆11丆俈丆俀丆俋丆俁丆俆丆13丆20丆15丆係丆10丆14丆19丆12丆18
慡俁係捠傝偺僫僀僩偺恑傔曽偼埲壓偺捠傝偱偡丅
俀亅俋亅俁亅俆亅13亅20亅15亅係亅10亅14亅19亅12亅18亅16亅俉亅侾亅俇亅17亅11亅俈 俀亅俋亅18亅16亅俉亅侾亅俇亅係亅10亅14亅19亅12亅俁亅俆亅13亅20亅15亅17亅11亅俈 俀亅俈亅11亅17亅俇亅侾亅俉亅16亅18亅12亅19亅14亅10亅係亅15亅20亅13亅俆亅俁亅俋 俀亅俈亅11亅17亅15亅20亅13亅俆亅俁亅12亅19亅14亅10亅係亅俇亅侾亅俉亅16亅18亅俋 俀亅俈亅11亅17亅俇亅侾亅俉亅16亅18亅俋亅俁亅俆亅13亅20亅15亅係亅10亅14亅19亅12 俀亅俈亅11亅17亅15亅20亅13亅俆亅俁亅俋亅18亅16亅俉亅侾亅俇亅係亅10亅14亅19亅12 俀亅俋亅俁亅俆亅13亅20亅15亅俈亅11亅17亅俇亅侾亅俉亅16亅18亅12亅19亅14亅10亅係 俀亅俋亅18亅16亅俉亅侾亅俇亅17亅11亅俈亅15亅20亅13亅俆亅俁亅12亅19亅14亅10亅係 俀亅俋亅俁亅俆亅13亅20亅15亅17亅11亅俈亅18亅16亅俉亅侾亅俇亅係亅10亅14亅19亅12 俀亅俋亅18亅16亅俉亅侾亅俇亅係亅10亅14亅19亅12亅俁亅俆亅13亅20亅15亅俈亅11亅17 俀亅俈亅11亅17亅俇亅侾亅俉亅16亅18亅俋亅俁亅12亅19亅14亅10亅係亅15亅20亅13亅俆 俀亅俈亅11亅17亅15亅20亅13亅俆亅俁亅俋亅18亅12亅19亅14亅10亅係亅俇亅侾亅俉亅16 俀亅俋亅俁亅俆亅13亅20亅15亅俈亅11亅17亅俇亅係亅10亅14亅19亅12亅18亅16亅俉亅侾 俀亅俋亅俁亅12亅19亅14亅10亅係亅俇亅侾亅俉亅16亅18亅俈亅11亅17亅15亅20亅13亅俆 俀亅俋亅俁亅俆亅13亅20亅15亅係亅10亅14亅19亅12亅18亅俈亅11亅17亅俇亅侾亅俉亅16 俀亅俋亅俁亅俆亅13亅20亅15亅17亅11亅俈亅18亅12亅19亅14亅10亅係亅俇亅侾亅俉亅16 俀亅俋亅18亅俈亅11亅17亅15亅20亅13亅俆亅俁亅12亅19亅14亅10亅係亅俇亅侾亅俉亅16 俀亅俋亅18亅16亅俉亅侾亅俇亅17亅11亅俈亅15亅係亅10亅14亅19亅12亅俁亅俆亅13亅20 俀亅俈亅11亅17亅15亅20亅13亅俆亅俁亅俋亅18亅16亅俉亅12亅19亅14亅10亅係亅俇亅侾 俀亅俈亅11亅17亅俇亅侾亅俉亅16亅18亅俋亅13亅20亅15亅係亅10亅14亅19亅12亅俁亅俆 俀亅俈亅11亅17亅俇亅侾亅俉亅16亅18亅12亅19亅14亅10亅係亅15亅20亅13亅俋亅俁亅俆 俀亅俈亅11亅17亅15亅20亅13亅俋亅18亅16亅俉亅侾亅俇亅係亅10亅14亅19亅12亅俁亅俆 俀亅俈亅11亅17亅俇亅侾亅俉亅12亅19亅14亅10亅係亅15亅20亅13亅俆亅俁亅俋亅18亅16 俀亅俈亅11亅17亅俇亅侾亅俉亅16亅18亅俋亅13亅俆亅俁亅12亅19亅14亅10亅係亅15亅20 俀亅俋亅俁亅俆亅13亅20亅15亅係亅10亅14亅19亅12亅俉亅16亅18亅俈亅11亅17亅俇亅侾 俀亅俋亅俁亅俆亅13亅20亅15亅俈亅11亅17亅俉亅16亅18亅12亅19亅14亅10亅係亅俇亅侾 俀亅俋亅俁亅俆亅13亅20亅15亅17亅11亅俈亅18亅16亅俉亅12亅19亅14亅10亅係亅俇亅侾 俀亅俋亅18亅16亅俉亅17亅11亅俈亅15亅20亅13亅俆亅俁亅12亅19亅14亅10亅係亅俇亅侾 俀亅俋亅13亅20亅15亅17亅11亅俈亅18亅16亅俉亅侾亅俇亅係亅10亅14亅19亅12亅俁亅俆 俀亅俋亅18亅16亅俉亅侾亅俇亅17亅11亅俈亅15亅20亅13亅係亅10亅14亅19亅12亅俁亅俆 俀亅俋亅俁亅俆亅13亅20亅15亅係亅10亅14亅19亅12亅俉亅侾亅俇亅17亅11亅俈亅18亅16 俀亅俋亅俁亅俆亅13亅20亅15亅俈亅11亅17亅俉亅侾亅俇亅係亅10亅14亅19亅12亅18亅16 俀亅俋亅俁亅俆亅13亅係亅10亅14亅19亅12亅18亅16亅俉亅侾亅俇亅17亅11亅俈亅15亅20 俀亅俋亅13亅俆亅俁亅12亅19亅14亅10亅係亅俇亅侾亅俉亅16亅18亅俈亅11亅17亅15亅20
丂仧 栤戣傊傕偳傞
丂仧 崱廡偺栤戣傊